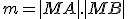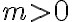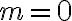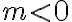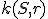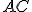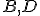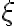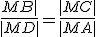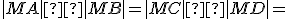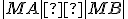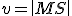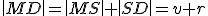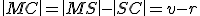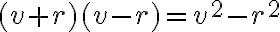Interaktívna geometria - planimetria
Kružnica, kruh
Mocnosť bodu ku kružnici
Je daná kružnica 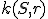 so stredom
so stredom  a polomerom
a polomerom 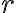 . Bod
. Bod  leží zvonka kružnice. Nech
leží zvonka kružnice. Nech 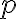 je sečnica
kružnice
je sečnica
kružnice 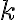 vedená bodom
vedená bodom  a
a  sú priesečníky sečnice s kružnicou
sú priesečníky sečnice s kružnicou 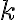 .
.
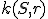 so stredom
so stredom  a polomerom
a polomerom 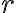 . Bod
. Bod  leží zvonka kružnice. Nech
leží zvonka kružnice. Nech 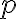 je sečnica
kružnice
je sečnica
kružnice 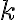 vedená bodom
vedená bodom  a
a  sú priesečníky sečnice s kružnicou
sú priesečníky sečnice s kružnicou 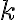 .
.
Skúmajme súčin 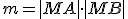 . Po otvorení motivačného appletu a experimentovaním s polohou bodu
. Po otvorení motivačného appletu a experimentovaním s polohou bodu  , môžeme vysloviť hypotézu:
, môžeme vysloviť hypotézu:
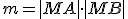 . Po otvorení motivačného appletu a experimentovaním s polohou bodu
. Po otvorení motivačného appletu a experimentovaním s polohou bodu  , môžeme vysloviť hypotézu:
, môžeme vysloviť hypotézu:
Otvorte si motivačný applet Tu.
Otázky.
Je súčin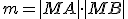 nezávislý od polohy sečnice
nezávislý od polohy sečnice 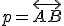 ? Inými slovami je konštantný pre ľubovoľnú polohu bodov
? Inými slovami je konštantný pre ľubovoľnú polohu bodov  ?
?
Môžeme definovať súčin aj pre prípad, ak bod leží vo vnútri kružnice
leží vo vnútri kružnice 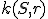 ? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
Je súčin
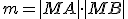 nezávislý od polohy sečnice
nezávislý od polohy sečnice 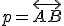 ? Inými slovami je konštantný pre ľubovoľnú polohu bodov
? Inými slovami je konštantný pre ľubovoľnú polohu bodov  ?
?
Môžeme definovať súčin aj pre prípad, ak bod
 leží vo vnútri kružnice
leží vo vnútri kružnice 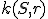 ? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
Definícia (Mocnosť bodu ku kružnici).
Ľubovoľnému bodu roviny možno priradiť reálne číslo
roviny možno priradiť reálne číslo 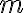 , pre ktorého absolútnu hodnotu platí
, pre ktorého absolútnu hodnotu platí 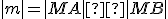 , pričom
, pričom
Ľubovoľnému bodu
 roviny možno priradiť reálne číslo
roviny možno priradiť reálne číslo 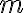 , pre ktorého absolútnu hodnotu platí
, pre ktorého absolútnu hodnotu platí 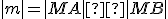 , pričom
, pričom
Dôkaz.
Dokázať tento dôsledok je veľmi jednoduché. Stačí zvoliť sečnicu 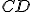 tak, aby prechádzala stredom kružnice. V takom prípade bude
tak, aby prechádzala stredom kružnice. V takom prípade bude
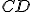 tak, aby prechádzala stredom kružnice. V takom prípade bude
tak, aby prechádzala stredom kružnice. V takom prípade bude
Poznámka.
V prípade, keď bod leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky
leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky 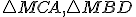 sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo
sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo 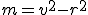 záporné. Pozrite si ilustračný obrázok.
záporné. Pozrite si ilustračný obrázok.
V prípade, keď bod
 leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky
leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky 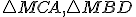 sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo
sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo 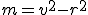 záporné. Pozrite si ilustračný obrázok.
záporné. Pozrite si ilustračný obrázok.
Nasledujúca veta platí len v prípade, že bod
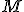 je mimo kružnice
je mimo kružnice  . Mocnosť bodu
. Mocnosť bodu 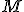 v tomto prípade môžeme vyjadriť
pomocou veľkosti úsečky
v tomto prípade môžeme vyjadriť
pomocou veľkosti úsečky 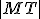 , kde
, kde 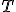 je dotykový bod dotyčnice ku kružnici, ktorá prechádza bodom
je dotykový bod dotyčnice ku kružnici, ktorá prechádza bodom 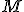 .
.
Veta 2.
Pre mocnosť bodu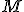 , ktorý leží zvonka kružnice
, ktorý leží zvonka kružnice 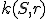 , platí rovnosť
, platí rovnosť 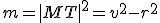 . Bod
. Bod 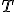 je dotykový bod dotyčnice, ktorá prechádza bodom
je dotykový bod dotyčnice, ktorá prechádza bodom  .
.
Pre mocnosť bodu
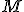 , ktorý leží zvonka kružnice
, ktorý leží zvonka kružnice 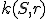 , platí rovnosť
, platí rovnosť 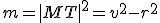 . Bod
. Bod 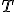 je dotykový bod dotyčnice, ktorá prechádza bodom
je dotykový bod dotyčnice, ktorá prechádza bodom  .
.
Dôkaz vety 2 ilustrujeme ako limitný prechod vo veta 1.
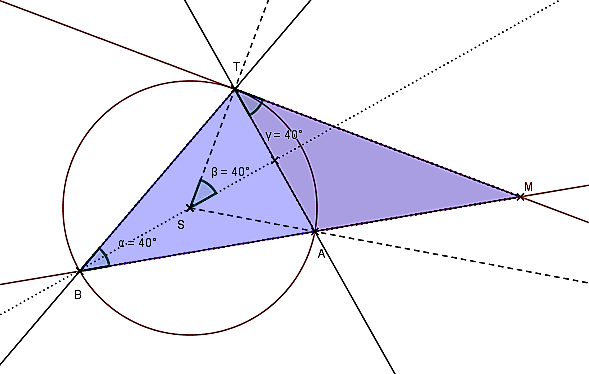 Pomocou obrázka urobte korektný matematický dôkaz. Využite podobnosť trojuholníkov
Pomocou obrázka urobte korektný matematický dôkaz. Využite podobnosť trojuholníkov 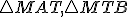 , ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí
, ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí 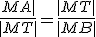 .
.
Pri odvodení vzťahu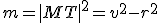 môžeme využiť skutočnosť, že trojuholník
môžeme využiť skutočnosť, že trojuholník 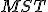 je pravouhlý a použiť Pytagorovu vetu.
je pravouhlý a použiť Pytagorovu vetu.
- Vzťah
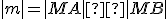 platí pro ľubovoľnú sečnicu.
platí pro ľubovoľnú sečnicu. - Pohybujme sečnicou tak, aby sa postupne blížila k dotyčnici v bode
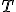 .
. - Bod
 i bod
i bod  sa blížia k bodu
sa blížia k bodu 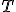 .
. - Veľkosť úsečky
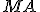 sa blíži k veľkosti úsečky
sa blíži k veľkosti úsečky 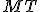 .
. - Z toho usudzujeme, že súčin
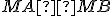 sa blíži k súčinu
sa blíži k súčinu 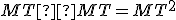 .
.

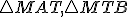 , ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí
, ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí 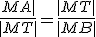 .
.
Pri odvodení vzťahu
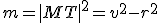 môžeme využiť skutočnosť, že trojuholník
môžeme využiť skutočnosť, že trojuholník 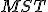 je pravouhlý a použiť Pytagorovu vetu.
je pravouhlý a použiť Pytagorovu vetu.
Definícia (Chordála a chordický bod).
Majme dve nesústredné kružnice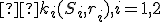 . Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
. Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
Majme dve nesústredné kružnice
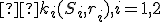 . Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
. Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
Korektnosť definície a konštrukcia chordály.
- Dané kružnice
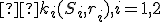 sa pretínajú v dvoch bodoch/priesečníkoch. Priamka určená priesečníkmi daných kružníc je spoločná sečnica oboch kružníc. Preto ľubovoľný bod priamky určenej týmito priesečníkmi má rovnakú mocnosť k obom kružniciam. Priamka určená priesečníkmi daných kružníc je chordála daných kružníc.
sa pretínajú v dvoch bodoch/priesečníkoch. Priamka určená priesečníkmi daných kružníc je spoločná sečnica oboch kružníc. Preto ľubovoľný bod priamky určenej týmito priesečníkmi má rovnakú mocnosť k obom kružniciam. Priamka určená priesečníkmi daných kružníc je chordála daných kružníc. - Kružnice sa dotýkajú v bode, ktorý má mocnosť
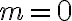 k obom kružniciam. Chordála je spoločná dotyčnica v bode. Dôkaz, že spoločná dotyčnica je množina bodov s rovnakou mocnosťou k obom kružniciam, vyplýva z vety 2.
k obom kružniciam. Chordála je spoločná dotyčnica v bode. Dôkaz, že spoločná dotyčnica je množina bodov s rovnakou mocnosťou k obom kružniciam, vyplýva z vety 2. - V prípade, že kružnice nemajú spoločný bod zvoľme pomocnú kružnicu
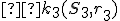 , ktorá pretína obe kružnice
, ktorá pretína obe kružnice 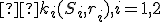 . Zostrojme chordály
. Zostrojme chordály 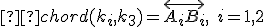 . Ich priesečník označme
. Ich priesečník označme 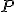 . Tento bod má rovnakú mocnosť ku všetkým trom kružniciam. Nazývame ho chordický bod. Týmto bodom potom vedieme kolmicu k úsečke, čo je chordála kružníc
. Tento bod má rovnakú mocnosť ku všetkým trom kružniciam. Nazývame ho chordický bod. Týmto bodom potom vedieme kolmicu k úsečke, čo je chordála kružníc 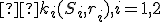 . Aktivujte si priložený applet.
. Aktivujte si priložený applet.