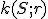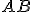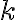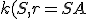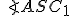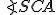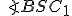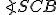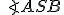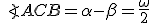Interaktívna geometria - planimetria
Kružnica, kruh
Veta o obvodových uholch
Veta (O obvodových uhloch).
Ľubovoľné dva obvodové uhly prislúchajúce k tomu istému oblúku kružnice majú rovnakú veľkosť.
Obvodový uhol je polovicou stredového uhla prislúchajúceho k tomu istému oblúku.
Ľubovoľné dva obvodové uhly prislúchajúce k tomu istému oblúku kružnice majú rovnakú veľkosť.
Obvodový uhol je polovicou stredového uhla prislúchajúceho k tomu istému oblúku.
-
Priložený applet je motivačný a môžete ho využiť pri skúmaní závislosti veľkosti obvodových uhlov
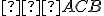 od polohy bodu
od polohy bodu  .
. -
Veľkosť obvodového uhla nezávisí od polohy bodu
 , rozhodujúce sú body
, rozhodujúce sú body 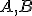 resp. uhol
resp. uhol 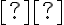 .
. - Konštrukcia oblúka, z ktorého vidieť úsečku pod daným uhlom. Otvorte si konštrukciu Tu.<\li>
- Ak body
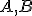 sú krajné body priemeru, tak rozdelia kružnicu na dve polkružnice: stredový uhol je priamy a obvodový uhol pravý.
sú krajné body priemeru, tak rozdelia kružnicu na dve polkružnice: stredový uhol je priamy a obvodový uhol pravý.
Dôkaz (vety o obvodových uhloch).
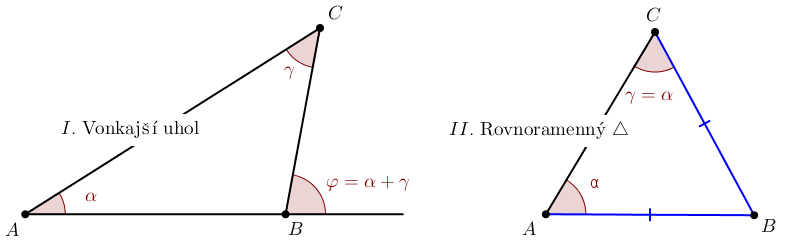
V dôkaze vety o obvodových uhloch sa využívajú dve základné vlastnosti trojuholníka.
Spojením týchto dvoch tvrdení dostaneme:
V dôkaze vety o obvodových uhloch sa využívajú dve základné vlastnosti trojuholníka.
- "Vonkajší uhol trojuholníka sa rovná súčtu vnútorných uhlov pri zvyšných vrcholoch."
- "V rovnoramennom trojuholníku sa uhly pri základni navzájom rovnajú" (Kniha 1, Tvrdenie V).
Spojením týchto dvoch tvrdení dostaneme:
Dôsledok.
Prípad 1 (Veta o obvodových uhloch).
Nech je vnútorný bod uhla
je vnútorný bod uhla 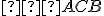 . Potom obvodový uhol
. Potom obvodový uhol 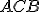 je polovicou stredového
uhla
je polovicou stredového
uhla 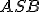 .
.
Nech
 je vnútorný bod uhla
je vnútorný bod uhla 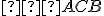 . Potom obvodový uhol
. Potom obvodový uhol 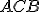 je polovicou stredového
uhla
je polovicou stredového
uhla 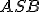 .
.
Prípad 2 (Veta o obvodových uhloch).
Nech leží na ramene uhla
leží na ramene uhla 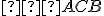 Potom obvodový uhol
Potom obvodový uhol 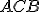 je tiež polovicou stredového uhla
je tiež polovicou stredového uhla 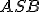 .
.
Nech
 leží na ramene uhla
leží na ramene uhla 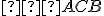 Potom obvodový uhol
Potom obvodový uhol 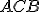 je tiež polovicou stredového uhla
je tiež polovicou stredového uhla 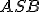 .
.
Posuňte bod C proti smeru hodinových ručičiek do krajnej polohy vľavo tak, aby body 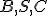 ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
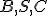 ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
Prípad 3 (Veta o obvodových uhloch).
Nech S je vonkajší bod uhla ∡ACB. Potom obvodový uhol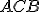 je polovicou stredového uhla
je polovicou stredového uhla 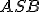 .
.
Nech S je vonkajší bod uhla ∡ACB. Potom obvodový uhol
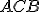 je polovicou stredového uhla
je polovicou stredového uhla 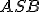 .
.
Zrejme platí 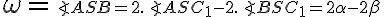 . Pozrime sa na rozdiel uhlov pri vrchole
. Pozrime sa na rozdiel uhlov pri vrchole 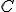 .
Zistíme, že
.
Zistíme, že 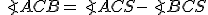 . Keďže trojuholníky
. Keďže trojuholníky 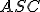 ,
, 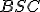 sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod
sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod 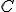 môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
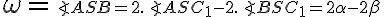 . Pozrime sa na rozdiel uhlov pri vrchole
. Pozrime sa na rozdiel uhlov pri vrchole 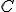 .
Zistíme, že
.
Zistíme, že 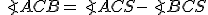 . Keďže trojuholníky
. Keďže trojuholníky 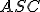 ,
, 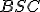 sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod
sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod 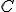 môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
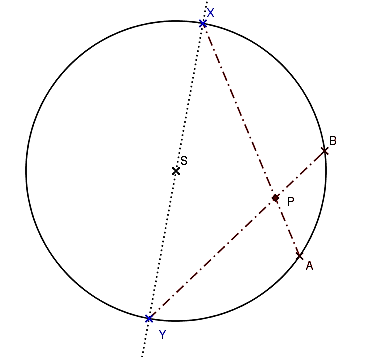
Príklad.
Je daná kružnica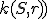 a na nej dva body
a na nej dva body 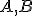 . Pre každý priemer
. Pre každý priemer
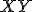 kružnice
kružnice  zostrojíme (ak existuje) priesečník priamok
zostrojíme (ak existuje) priesečník priamok 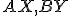 .
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že
.
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že 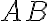 nie je priemer kružnice. (Larson 8.1.2.)
nie je priemer kružnice. (Larson 8.1.2.)
Je daná kružnica
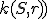 a na nej dva body
a na nej dva body 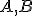 . Pre každý priemer
. Pre každý priemer
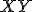 kružnice
kružnice  zostrojíme (ak existuje) priesečník priamok
zostrojíme (ak existuje) priesečník priamok 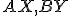 .
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že
.
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že 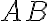 nie je priemer kružnice. (Larson 8.1.2.)
nie je priemer kružnice. (Larson 8.1.2.)
V planimetrii sa pomerne často vyskytujú úlohy, v ktorých sa hľadá množina  bodov s danou vlastnosťou
bodov s danou vlastnosťou 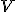 .
Symolicky to môžeme zapísať takto
.
Symolicky to môžeme zapísať takto 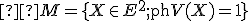 . Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
. Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
 je kružnicový oblúk
je kružnicový oblúk 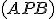 . Na overenie platnosti výroku "
. Na overenie platnosti výroku "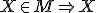 má vlastnosť
má vlastnosť 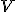 " teraz stačí ukázať, že výroková formula
" teraz stačí ukázať, že výroková formula ![[(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.) [(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.)](https://lms.umb.sk/filter/tex/pix.php/1d2466a43806dc0ae93b0078ee6c0d9a.png) je tautológia. To je však zrejmé. Keďže aj opačný postup
je tautológia. To je však zrejmé. Keďže aj opačný postup ![[(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1. [(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1.](https://lms.umb.sk/filter/tex/pix.php/af5824de788b473b6bd4ab77ebe529d5.png) je tautológia, tak aj časť C je pravdivý výrok.
je tautológia, tak aj časť C je pravdivý výrok.
 bodov s danou vlastnosťou
bodov s danou vlastnosťou 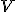 .
Symolicky to môžeme zapísať takto
.
Symolicky to môžeme zapísať takto 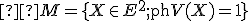 . Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
. Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
- Najskôr musíme určiť základné charakteristické prvky danej množiny (najčastejšie experimentálne) resp. komplexne popísať danú množinu
 .
Potom overiť platnosť výrokov:
.
Potom overiť platnosť výrokov: 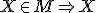 má vlastnosť
má vlastnosť 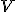 ,
, - ak
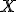 má vlastnosť
má vlastnosť 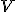 , tak patrí do množiny
, tak patrí do množiny  .
.
- Thalesova veta hovorí, že trojuholníky
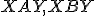 sú pravouhlé s pravým uhlom pri vrcholoch
sú pravouhlé s pravým uhlom pri vrcholoch 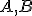 .
. - Obvodové uhly
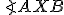 a
a 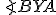 majú rovnakú veľkosť
majú rovnakú veľkosť  .
. - Označme si
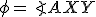 a
a 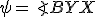 .
. - Súčet uhlov v trojuholníku je 180°, preto
bude
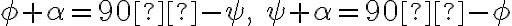 .
. - Odtiaľ dostávame, že súčet uhlov
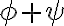 je konštantný pre ľubovoľný priemer
je konštantný pre ľubovoľný priemer 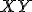 a dva pevné body
a dva pevné body 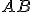 .
. - Preto aj vrcholové uhly
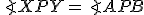 majú konštantnú veľkosť. To znamená, že body
majú konštantnú veľkosť. To znamená, že body  ležia na kružnicovom oblúku
ležia na kružnicovom oblúku
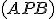 .
. - K nájdeniu oblúka stačí zvoliť jeden priemer
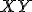 a jeden odpovedajúci priesečník
a jeden odpovedajúci priesečník 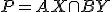 .
.
 je kružnicový oblúk
je kružnicový oblúk 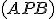 . Na overenie platnosti výroku "
. Na overenie platnosti výroku "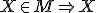 má vlastnosť
má vlastnosť 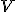 " teraz stačí ukázať, že výroková formula
" teraz stačí ukázať, že výroková formula ![[(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.) [(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.)](https://lms.umb.sk/filter/tex/pix.php/1d2466a43806dc0ae93b0078ee6c0d9a.png) je tautológia. To je však zrejmé. Keďže aj opačný postup
je tautológia. To je však zrejmé. Keďže aj opačný postup ![[(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1. [(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1.](https://lms.umb.sk/filter/tex/pix.php/af5824de788b473b6bd4ab77ebe529d5.png) je tautológia, tak aj časť C je pravdivý výrok.
je tautológia, tak aj časť C je pravdivý výrok.
Poznámky.
- Pri určovaní GMB je mnohokrát najťažší krok A.
- Program GeoGebra tento krok zjednoduší tým, že pomocou nástroja "Množina bodov" (nachádza sa v sekcii nástrojov "Kolmica") vykreslí hľadanú
množinu
 .
. - Potom je však nutné realizovať kroky B a C.
- Pozrite si aplikovanie tohto nástroja v kurze Didaktika matematiky v knihe Množiny bodov. Dostupné Tu.