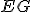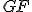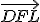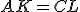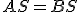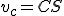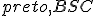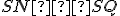Interaktívna geometria - planimetria
Zhodnosť a podobnosť trojuholníkov
Vety o zhodnosti trojuholníkov
Veta (o zhodnosti trojuholníkoch).
- (sus) Trojuholníky, ktoré sa zhodujú v dvoch stranách a uhle nimi zovretom sú zhodné.
- (sss) Trojuholníky, ktoré sa zhodujú v troch stranách sú zhodné.
- (usu) Ak sa dva trojuholníky zhodujú v jednej strane a v dvoch uhloch priľahlých, tak sú zhodné.
- (Ssu) Ak sa dva trojuholníky zhodujú v dvoch stranách a v uhle oproti väčšej strane, tak sú zhodné.
Poznámka.
Uvedieme len dôkazy prvých dvoch viet tak, ako sú uvedené v Euklidových Základoch. Dôkazy viet (usu) a (Ssu) prenechávame čitateľovi ako cvičenie. Vyhľadajte v Základoch tieto vety a upravte Euklidove dôkazy tak, aby boli v súlade s modernou terminológiou.
Dôkaz.
Uvedieme len dôkazy prvých dvoch viet tak, ako sú uvedené v Euklidových Základoch. Dôkazy viet (usu) a (Ssu) prenechávame čitateľovi ako cvičenie. Vyhľadajte v Základoch tieto vety a upravte Euklidove dôkazy tak, aby boli v súlade s modernou terminológiou.
- Euklidových Základoch je veta sformulovaná ako
Proposition 4 (Euclid's Elements, Book I ).
- Nech
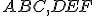 sú dva trojuholníky, ktoré majú dve strany
sú dva trojuholníky, ktoré majú dve strany 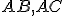 rovné dvom stranám
rovné dvom stranám 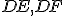 .
Konkrétne
.
Konkrétne 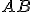 rovná
rovná 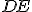 a
a 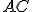 rovná
rovná 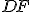 a uhol
a uhol 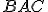 je rovný uhlu
je rovný uhlu 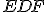 .
.
- Hovorím (Euklides), že základňa
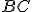 sa rovná aj základni
sa rovná aj základni 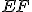 , trojuholník
, trojuholník  sa rovná
trojuholníku
sa rovná
trojuholníku 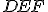 a zostávajúce uhly sa rovnajú zostávajúcim uhlom, respektíve opačne rovnakým stranám. To znamená, že
uhol
a zostávajúce uhly sa rovnajú zostávajúcim uhlom, respektíve opačne rovnakým stranám. To znamená, že
uhol  sa rovná uhlu
sa rovná uhlu 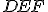 a uhol
a uhol 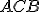 sa rovná uhlu
sa rovná uhlu 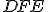 .
Nepriamy dôkaz
.
Nepriamy dôkaz
- Nech trojuholník
 je uložený na trojuholníku
je uložený na trojuholníku 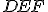 a ak je bod
a ak je bod  umiestnený na bode
umiestnený na bode
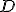 a priamka
a priamka 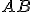 na
na 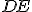 .
.
- Priamka
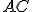 sa tiež rovná
sa tiež rovná 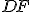 , pretože uhol
, pretože uhol 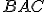 sa rovná uhlu
sa rovná uhlu 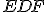 .
. - Ale
 sa tiež zhoduje s
sa tiež zhoduje s 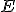 , a preto základňa
, a preto základňa 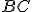 sa zhoduje so základňou
sa zhoduje so základňou 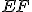 a rovná sa jej.
a rovná sa jej. - Takže celý trojuholník
 sa zhoduje s celým trojuholníkom
sa zhoduje s celým trojuholníkom 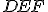 a rovná sa.
a rovná sa. - Zvyšné uhly sa zhodujú so zostávajúcimi uhlami a rovnajú sa, uhol
 sa rovná uhlu
sa rovná uhlu 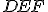 a uhol
a uhol 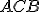 sa rovná uhlu
sa rovná uhlu 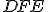 .
. -
Preto ak dva trojuholníky majú dve strany rovnobežné s dvoma stranami a majú uhly obsiahnuté rovnými čiarami rovnaké, potom majú aj základňu rovnú základni,
trojuholník sa rovná trojuholníku a zvyšné uhly sú rovné zvyšným uhlom respektíve tým, ktoré sú oproti rovnakým stranám.
Ilustračný obrázok vety (sus).
- Nech
- V Euklidových Základoch je veta sss sformulovaná ako Proposition 8 (Euclid's Elements, Book I ).
- Nech trojuholník
 je prenesený na trojuholník
je prenesený na trojuholník 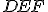 tak, aby bod
tak, aby bod  bol umiestnený na bode
bol umiestnený na bode 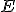 a priamka
a priamka 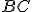 na
na 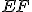 .
.
- Potom bod
 sa prekrýva (zhoduje) s bodom
sa prekrýva (zhoduje) s bodom 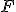 , pretože
, pretože 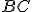 sa rovná
sa rovná 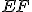 .
. - Ukážeme, že aj úsečka
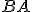 resp.
resp. 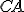 sa prekrýva (zhoduje) s úsečkou
sa prekrýva (zhoduje) s úsečkou 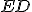 resp.
resp. 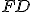 .
Budeme dokazovať nepriamo.
.
Budeme dokazovať nepriamo.
- Keďže trojuholník
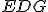 je rovnoramenný, tak uhol
je rovnoramenný, tak uhol 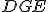 rovná uhlu
rovná uhlu 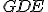 .
. - Z polohy bodu
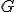 vyplýva, že uhol
vyplýva, že uhol
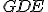 je väčší ako uhol
je väčší ako uhol 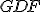 .
. - Tiež trojuholník
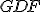 je rovnoramenný, preto aj uhol
je rovnoramenný, preto aj uhol 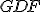 rovná uhlu
rovná uhlu 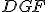 .
. - Z polohy bodu
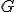 vyplýva, že uhol
vyplýva, že uhol 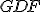 väčší ako uhol
väčší ako uhol 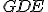 , čo je spor.
, čo je spor. - Preto musí byť bod
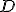 totožný s bodom
totožný s bodom 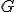 .
. - Podobne postupujeme v prípade, ak bod
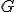 bude v polrovine
bude v polrovine 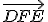 .
.
- Ukázali sme, že strana
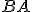 resp.
resp. 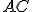 sa prekrýva so stranou
sa prekrýva so stranou 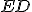 resp.
resp.
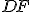 . To znamená, že uhol
. To znamená, že uhol 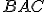 sa rovná uhlu
sa rovná uhlu 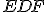 .
.
- Teraz stačí použiť vetu
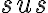 a dostávame tvrdenie: trojuholníky
a dostávame tvrdenie: trojuholníky  a
a 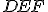 sú zhodné.
sú zhodné.
- Nech trojuholník
Vety o zhodnosti trojuholníkov sa využívajú hlavne v úlohách, v ktorých sa skúmajú a dokazujú špecifické vlastnosti geometrických útvarov. Uvedieme niekoľko takých úloh.
Príklad 1. (Veta sus)
Je daný obdĺžnik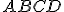 . Nech body
. Nech body 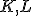 , sú bodmi uhlopriečky
, sú bodmi uhlopriečky 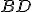 , pre ktoré platí
, pre ktoré platí 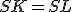 .
.
Dokážte, že trojuholníky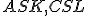 sú zhodné.
sú zhodné.
Je daný obdĺžnik
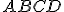 . Nech body
. Nech body 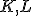 , sú bodmi uhlopriečky
, sú bodmi uhlopriečky 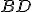 , pre ktoré platí
, pre ktoré platí 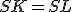 .
.
Dokážte, že trojuholníky
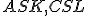 sú zhodné.
sú zhodné.
Ľahko sa presvedčíme, že trojuholníky 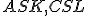 sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
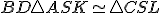 .
.
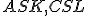 sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
-
bod
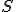 je stred uhlopriečky (uhlopriečky v obdĺžniku sa rozpoľujú)
je stred uhlopriečky (uhlopriečky v obdĺžniku sa rozpoľujú) - uhly
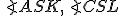 sú vrcholové, preto sú zhodné
sú vrcholové, preto sú zhodné
- úsečky
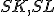 sú podľa predpokladu zhodné
sú podľa predpokladu zhodné
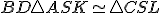 .
.
Príklad 2. (Veta sss)
Narysujte ľubovoľný rovnoramenný trojuholník so základňou
so základňou 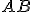 . Zostrojte stred
. Zostrojte stred  strany
strany
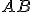 . Čo platí pre trojuholníky
. Čo platí pre trojuholníky 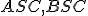 ? Ukážte, že platí
? Ukážte, že platí
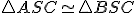 .
.
V trojuholníkoch Narysujte ľubovoľný rovnoramenný trojuholník
 so základňou
so základňou 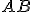 . Zostrojte stred
. Zostrojte stred  strany
strany
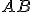 . Čo platí pre trojuholníky
. Čo platí pre trojuholníky 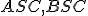 ? Ukážte, že platí
? Ukážte, že platí
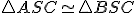 .
.
 odpovedajúce strany majú rovnakú dĺžku. Keďže
odpovedajúce strany majú rovnakú dĺžku. Keďže
Poznámky.
- Tháles: V rovnoramennom trojuholníku uhly pri základni sú zhodné.
- Euklides: Základy/Proposition 5 (Euclid's Elements, Book I. )
Príklad 3. (Veta Ssu)
Na osi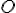 ostrého uhla
ostrého uhla  zostrojte vnútri uhla
zostrojte vnútri uhla 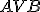 bod
bod 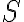 . Zostrojte kružnicu
. Zostrojte kružnicu 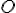
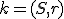 tak, aby platilo
tak, aby platilo 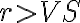 .
.
Označte priesečníky priamky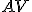 s kružnicou
s kružnicou  ako
ako 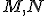 a priesečníky priamky
a priesečníky priamky
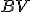 s kružnicou
s kružnicou  ako
ako 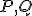 .
.
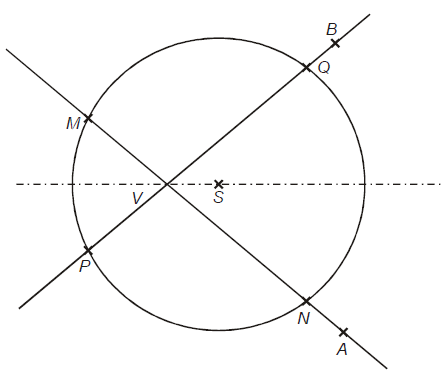
Dokážte, že úsečky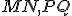 majú rovnakú veľkosť.
majú rovnakú veľkosť.
Na osi
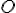 ostrého uhla
ostrého uhla 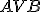 zostrojte vnútri uhla
zostrojte vnútri uhla 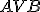 bod
bod 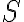 . Zostrojte kružnicu
. Zostrojte kružnicu 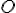
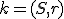 tak, aby platilo
tak, aby platilo 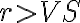 .
.
Označte priesečníky priamky
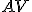 s kružnicou
s kružnicou  ako
ako 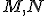 a priesečníky priamky
a priesečníky priamky
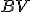 s kružnicou
s kružnicou  ako
ako 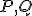 .
.
Dokážte, že úsečky
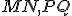 majú rovnakú veľkosť.
majú rovnakú veľkosť.
Analýza úlohy.
-
Najskôr sa pokúste dokázať rovnosť
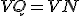 pomocou zhodnosti trojuholníkov:
pomocou zhodnosti trojuholníkov: 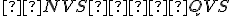 .
Pre tieto trojuholníky platí:
.
Pre tieto trojuholníky platí:
-
Potom dokážte rovnosť
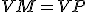 pomocou zhodnosti trojuholníkov:
pomocou zhodnosti trojuholníkov: 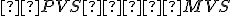 .
.
Pre tieto trojuholníky platí:- strana
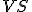 je spoločná obom trojuholníkom
je spoločná obom trojuholníkom -
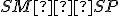 (polomery kružnice
(polomery kružnice  )
)
-
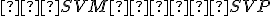 (súčet zhodných vrcholových uhlov a polovíc uhla
(súčet zhodných vrcholových uhlov a polovíc uhla 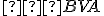 )
)
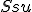 , preto aj tretie strany sú zhodné:
, preto aj tretie strany sú zhodné:
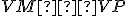
- strana
-
K ukončeniu dôkazu si stačí uvedomiť, že úsečky
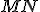 a
a 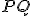 získame sčítaním dvoch dvojíc
zhodných úsečiek, platí
získame sčítaním dvoch dvojíc
zhodných úsečiek, platí 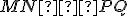 .
.
Záver. Trojuholníky sú zhodné podľa vety
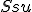 , preto aj tretie strany sú zhodné:
, preto aj tretie strany sú zhodné:
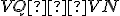 .
.
Príklad 4.
...
...
...
obr
Otvorte
...
Otvorte