Interaktívna geometria - planimetria
Geometria trojuholníka
Pytagorova a Euklidove vety
Veta (Pytagorova veta).
V každom pravouhlom trojuholníku , v ktorom prepona má veľkosť
, v ktorom prepona má veľkosť  a odvesny majú veľkosti
a odvesny majú veľkosti  platí
platí
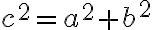 .
.
V každom pravouhlom trojuholníku
 , v ktorom prepona má veľkosť
, v ktorom prepona má veľkosť  a odvesny majú veľkosti
a odvesny majú veľkosti  platí
platí
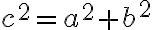 .
.
Slovná formulácia Pytagorovej vety:
Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
Pytagorova veta je pomenovaná podľa starogréckeho matematika Pytagora, ktorý ju odvodil v 6. storočí pred Kr.
Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
Pytagorova veta je pomenovaná podľa starogréckeho matematika Pytagora, ktorý ju odvodil v 6. storočí pred Kr.
- Dôkazov Pytagorovej vety existuje veľmi veľa, viac ako 300, pozri na GeoGebre Tu.
- Vyhľadajte pôvodný Euklidov dôkaz v Knihe I, tvrdenie T/XLVII)
- Pozrite si dôkaz Pytagorovej vety v programe GeoGebra, ktorý vychádza z Euklidovho dôkazu. Otvorte si applet Tu.
- Iné dôkazy Pytagorovej vety nájdeme na stránke M. Viklera alebo Wikipedia.
- Dôkaz "bez slov" →. Doplňte "slová" pre tento dôkaz - urobte slovné/písomné zdôvodnenie.
Poznámky.
- Pytagorova veta pravdepodobne bola známa aj v iných starovekých civilizáciách, napríklad v Číne, Egypte.
- Starí Egypťania stavali pozoruhodné stavby, pri ktorých potrebovali vytyčovať aj pravé uhly. Robili to takto:
Veta (Obrátená pytagorova veta).
Ak v trojuholníku platí pre dĺžky strán
platí pre dĺžky strán 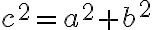 , tak tento trojuholník je pravouhlý s preponou
, tak tento trojuholník je pravouhlý s preponou  .
.
Ak v trojuholníku
 platí pre dĺžky strán
platí pre dĺžky strán 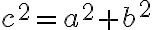 , tak tento trojuholník je pravouhlý s preponou
, tak tento trojuholník je pravouhlý s preponou  .
.
Príklad.
Dané sú sústredné kružnice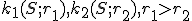 . Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami
. Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami 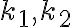 a obsahom kruhu nad tetivou
a obsahom kruhu nad tetivou 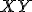 kružnice
kružnice 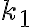 , ktorá sa dotýka kružnice
, ktorá sa dotýka kružnice 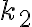 .
Riešenie
.
Riešenie
Preskúmajte súvislosť tejto úlohy s dôkazom Pytagorovej vety aplikáciou Mamikonovej vety (Wiki odkaz Tu). Otvorte si applet Tu
Dané sú sústredné kružnice
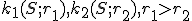 . Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami
. Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami 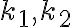 a obsahom kruhu nad tetivou
a obsahom kruhu nad tetivou 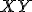 kružnice
kružnice 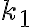 , ktorá sa dotýka kružnice
, ktorá sa dotýka kružnice 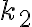 .
Riešenie
.
Riešenie
Preskúmajte súvislosť tejto úlohy s dôkazom Pytagorovej vety aplikáciou Mamikonovej vety (Wiki odkaz Tu). Otvorte si applet Tu
Pytagorova veta uvedená v Euklidových Základoch: Kniha 1, tvrdenie XLVII).
Veta (Pytagorova veta - znenie uvedené v Základoch).
V pravouhlých trojuholníkoch štvorec na strane oproti pravému uhlu ležiaci je rovný súčtu štvorcov na stranách, ktoré zvierajú pravý uhol.
V pravouhlých trojuholníkoch štvorec na strane oproti pravému uhlu ležiaci je rovný súčtu štvorcov na stranách, ktoré zvierajú pravý uhol.
Text Euklidovho dôkazu je spracovaný podľa českého prekladu od Františka Servíta z roku 1907, je doplnený o
(odkazy) na definície (Def.), axiómy (Post.), tvrdenia (T.) a Koncepcie / Zásady (Kon.)
Dôkaz.
-
 je pravouhlý trojuholník s pravým uhlom
je pravouhlý trojuholník s pravým uhlom 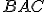 .
Hovorím, že štvorec na
.
Hovorím, že štvorec na 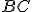 sa rovná (súčtom) štvorcov na
sa rovná (súčtom) štvorcov na 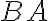 a
a 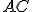 .
. - Nech je narysovaný
-
Bodom
 je vedená rovnobežka
je vedená rovnobežka 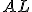 k
k 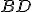 alebo k
alebo k
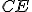 (T.31) a spojnice (úsečky)
(T.31) a spojnice (úsečky) 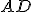 a
a 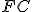 .
(Post.1)
.
(Post.1)
-
Vzhľadom na to, že každý z uhlov
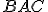 a
a 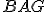 je pravý, z toho vyplýva, že priamkou
je pravý, z toho vyplýva, že priamkou
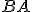 a bodom
a bodom  na ňom dve priame línie
na ňom dve priame línie 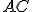 a
a 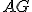 , ktoré nie sú
ležiace na tej istej strane, spôsobujú, že susedné uhly sa rovnajú dvom pravým uhlom
(Def.22)
, ktoré nie sú
ležiace na tej istej strane, spôsobujú, že susedné uhly sa rovnajú dvom pravým uhlom
(Def.22)
- Pretože uhol
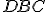 sa rovná uhlu
sa rovná uhlu 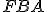 , pretože každý je pravý
(Post.4)
, pretože každý je pravý
(Post.4)
- Keďže
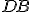 sa rovná
sa rovná 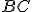 a
a 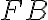 sa rovná
sa rovná
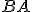 (Def.22),
(Def.22),
-
obe strany
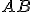 a
a 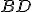 sa rovnajú obom stranám
sa rovnajú obom stranám 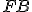 a
a  a
a
uhol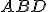 sa rovná uhlu
sa rovná uhlu 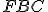 , preto základňa
, preto základňa 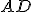 sa rovná základni
sa rovná základni 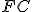 a
a
trojuholník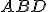 sa rovná (je zhodný) trojuholníku
sa rovná (je zhodný) trojuholníku 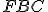 .
(T.4)
.
(T.4)
- Teraz rovnobežník
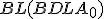 je dvakrát väčší ako trojuholník
je dvakrát väčší ako trojuholník
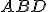 , pretože majú rovnakú základňu
, pretože majú rovnakú základňu 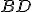 a
a
sú medzi tými istými rovnobežkami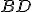 a
a 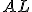 (majú spoločnú výšku).
(T.41)
(majú spoločnú výšku).
(T.41)
- A štvorec
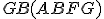 je dvakrát väčší ako trojuholník
je dvakrát väčší ako trojuholník
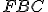 , pretože opäť majú rovnakú základňu
, pretože opäť majú rovnakú základňu 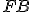 a
a
sú medzi tými istými rovnobežkami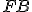 a
a 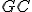 .
(T.41)
.
(T.41) - Preto sa rovnobežník
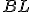 rovná štvorcu
rovná štvorcu 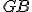 .
(Kon.2)
.
(Kon.2)
- Podobne, ak vedieme spojnice (úsečky)
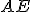 a
a
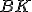 , rovnobežník
, rovnobežník 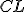 sa rovná štvorcu
sa rovná štvorcu  . Preto sa celý štvorec
. Preto sa celý štvorec
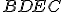 rovná súčtu dvoch štvorcov
rovná súčtu dvoch štvorcov 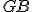 a
a 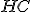 .
(Kon.2)
.
(Kon.2) -
A štvorec
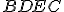 je narysovaný na
je narysovaný na 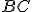 a štvorce
a štvorce 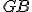 a
a 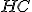 na
na
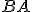 a
a 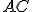 . Teda štvorec na
. Teda štvorec na 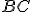 sa rovná súčtu štvorcov na
sa rovná súčtu štvorcov na 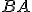 a
a 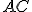 .
.
V dôkaze boli použité tieto zdroje z Euklidových Základov:
- Definícia 22: Zo štvorstranných útvarov je štvorec, ktorý je rovnako rovnostranný a pravouhlý; obdĺžnik, ktorý je pravouhlý, ale nie rovnostranný; kosoštvorec, ktorý je rovnostranný, ale nie pravouhlý; kosodĺžnik, ktorý má opačné strany a uhly rovno navzájom, ale nie je ani rovnostranný, ani pravouhlý. Okrem týchto sú to štvoruholníky, ktoré sa nazývajú lichobežníky (rôznobežníky).
- Postulát 1: Nech je úlohou nakresliť priamku z ktoréhokoľvek bodu do ktoréhokoľvek bodu. Tento prvý postulát hovorí, že vzhľadom na akékoľvek dva body, ako sú A a B, existuje priamka AB, ktorá ich má ako koncové body. (Porovnaj s postulátom 5).
- Postulát 4: To, že všetky pravé uhly sa navzájom rovnajú.
- Tvrdenie 4: Ak dva trojuholníky majú dve strany rovnajúce sa dvom stranám a majú uhly obsiahnuté v rovnakých rovných priamkach rovnaké, potom majú tiež základňu rovnú základni, trojuholník sa rovná trojuholníku a zostávajúce uhly sa rovnajú zostávajúcim uhlom respektíve, a síce oproti rovnakým stranám. Veta o zhodnosti trojuholníkov - sus
- Tvrdenie 14: Ak na priamke a v bode na nej sú dve priamky, ktoré neležia na tej istej strane, sa súčet susedných uhlov rovná dvom pravým uhlom, potom sú tieto dve priamky navzájom k sebe v priamke (tvoria jednu priamku). Tvrdenie 31 Vytvor priamku cez daný bod rovnobežne s danou priamkou.
- Tvrdenie 41: Ak rovnobežník má rovnakú základňu s trojuholníkom a je medzi tými istými rovnobežkami, rovnobežník je dvakrát väčší ako trojuholník.
- Tvrdenie 46: Na danej priamke narysuj štvorec. (Súčasná matematická formulácia tejto vety: Nad danou úsečkou je možné narysovať štvorec.)
- Koncepcia/Zásada 2: Ak sú rovnosti pridané do rovnováhy, potom celky sú rovnaké.
- Koncepcia/Zásada 5: Celok je väčší než časť.
Cvičenie.
Vytvorte si vlastný applet, ktorým budete interpretovať Euklidov dôkaz Pytagorovej vety. Pozrite si náš návrh:
Vytvorte si vlastný applet, ktorým budete interpretovať Euklidov dôkaz Pytagorovej vety. Pozrite si náš návrh:
Veta (Euklidova veta o výške).
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony.
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony.
Dôkaz.
Nech v pravouhlom trojuholníku s pravým uhlom pri vrchole
s pravým uhlom pri vrchole  je
je 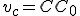 výška na preponu
výška na preponu 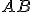 .
.
Zrejme platí:
Z podobnosti trojuholníkov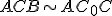 a
a 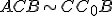 vyplýva:
vyplýva:
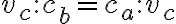 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 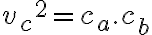 .
.
Tým je dôkaz Euklidovej vety o výške ukončený. Dôkaz, ktorý využíva zhodnosť od Vinklera nájdete Tu.
Nech v pravouhlom trojuholníku
 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole  je
je 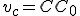 výška na preponu
výška na preponu 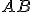 .
.
Zrejme platí:
- výška
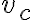 pravouhlého trojuholníka rozdelí trojuholník na ďalšie dva pravouhlé trojuholníky,
pravouhlého trojuholníka rozdelí trojuholník na ďalšie dva pravouhlé trojuholníky, - päta výšky
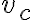 rozdelí preponu na dva úseky priľahlé k odvesnám trojuholníka:
rozdelí preponu na dva úseky priľahlé k odvesnám trojuholníka: 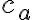 a
a 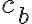 ,
, - zo vzťahu
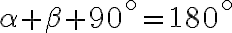 dostávame
dostávame 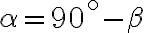 ,
, - všetky tri vzniknuté trojuholníky sú navzájom podobné:
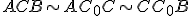 .
.
Z podobnosti trojuholníkov
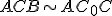 a
a 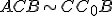 vyplýva:
vyplýva:
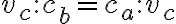 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 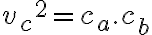 .
.
Tým je dôkaz Euklidovej vety o výške ukončený. Dôkaz, ktorý využíva zhodnosť od Vinklera nájdete Tu.
Veta (Euklidova veta o odvesne).
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a priľahlého úseku.
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a priľahlého úseku.
Dôkaz.
Z podobnosti trojuholníkov a
a 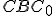 vyplýva:
vyplýva: 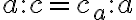 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 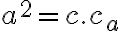 .
.
Z podobnosti trojuholníkov a
a 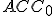 odvodíme druhú Euklidovu vetu
odvodíme druhú Euklidovu vetu 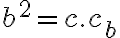 .
.
Z podobnosti trojuholníkov
 a
a 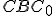 vyplýva:
vyplýva: 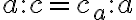 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 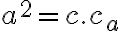 .
.
Z podobnosti trojuholníkov
 a
a 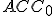 odvodíme druhú Euklidovu vetu
odvodíme druhú Euklidovu vetu 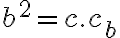 .
.
Cvičenie.
Dokážte Pytagorovu vetu pomocou Euklidových viet.
Dokážte Pytagorovu vetu pomocou Euklidových viet.