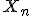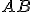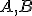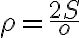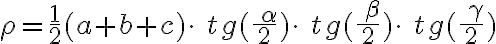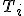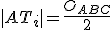Interaktívna geometria - planimetria
Geometria trojuholníka
Trojuholníkové centrum
Definícia.
Bod trojuholníka, ktorý je invariantný vzhľadom na rovnoľahlosť, sa nazýva trojuholníkové centrum (triangle Center).
Bod trojuholníka, ktorý je invariantný vzhľadom na rovnoľahlosť, sa nazýva trojuholníkové centrum (triangle Center).
Najznámejšie sú napríklad
Menej známe ale často využívané v konštrukciách sú Eulerova priamka a Feurbachova kružnica deviatich bodov.
Definícia (Eulerova priamka).
V ľubovoľnom trojuholníku, s výnimkou rovnostranného, ležia ortocentrum , ťažisko
, ťažisko  a stred opísanej kružnice
a stred opísanej kružnice
 S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí
S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí 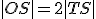 . V rovnostrannom trojuholníku body
. V rovnostrannom trojuholníku body
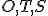 splývajú.
splývajú.
V ľubovoľnom trojuholníku, s výnimkou rovnostranného, ležia ortocentrum
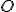 , ťažisko
, ťažisko 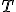 a stred opísanej kružnice
a stred opísanej kružnice
 S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí
S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí 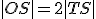 . V rovnostrannom trojuholníku body
. V rovnostrannom trojuholníku body
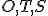 splývajú.
splývajú.
Pozrite si dôkaz od Martina Vinklera, prípadne navrhnite iný dôkaz s využitím rovnoľahlosti Tu.
Definícia (Feuerbachova kružnica).
Nech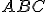 je všeobecný trojuholník,
je všeobecný trojuholník, 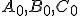 nech sú päty jeho výšok,
nech sú päty jeho výšok, 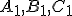 nech sú
stredy jeho strán,
nech sú
stredy jeho strán, 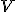 nech je priesečník výšok a
nech je priesečník výšok a 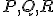 nech sú postupne stredy úsečiek
nech sú postupne stredy úsečiek 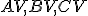 .
Potom
.
Potom 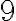 bodov
bodov 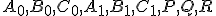 leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
Nech
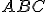 je všeobecný trojuholník,
je všeobecný trojuholník, 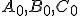 nech sú päty jeho výšok,
nech sú päty jeho výšok, 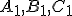 nech sú
stredy jeho strán,
nech sú
stredy jeho strán, 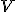 nech je priesečník výšok a
nech je priesečník výšok a 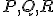 nech sú postupne stredy úsečiek
nech sú postupne stredy úsečiek 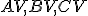 .
Potom
.
Potom 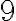 bodov
bodov 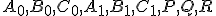 leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
Definícia.
Kružnica, ktorá prechádza všetkými troma vrcholmi trojuholníka sa nazýva kružnica opísaná trojuholníku.
Kružnica, ktorá prechádza všetkými troma vrcholmi trojuholníka sa nazýva kružnica opísaná trojuholníku.
Konštrukčne pri hľadaní stredu opísanej kružnice postupujme takto:
- Zvolíme si ľubovoľné dve strany trojuholníka a zostrojíme ich osi .
- Priesečník týchto osí je stred
 kružnice opísanej trojuholníku
kružnice opísanej trojuholníku  .
. - Zároveň je nutné dokázať, že os tretej strany trojuholníka
 prechádza vždy týmto priesečníkom.
prechádza vždy týmto priesečníkom.
(dôkaz už poznal Tháles)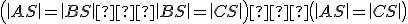 .
. - Z tejto konštrukcie vyplýva aj tvrdenie, že každému trojuholníku možno opísať práve jednu kružnicu.
- Kde leží stred kružnice opísanej u pravouhlých trojuholníkov?
Dôkaz uvádza Euklides v Knihe 1, Tvrdenie X., pozri kapitolu "Euklidovské konštrukcie".
Definícia.
-
Kružnica opísaná pravouhlému trojuholníku sa nazýva Tálesova kružnica.
Vlastnosti kružnice opísanej trojuholníku.
-
Veľkosť polomeru opísanej kružnice určuje vzťah
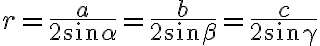
- Spojnica stredu opísanej kružnice a vrcholu trojuholníka je kolmá k strane jeho ortického trojuholníka (tzv. Nagelova veta →).
-
Kružnica deviatich bodov je rovnoľahlým obrazom opísanej kružnice so stredom rovnoľahlosti v ťažisku trojuholníka a koeficientom
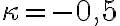 .
.
Definícia.
Ak z ľubovoľného bodu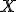 opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod
opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod 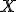 spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
Ak z ľubovoľného bodu
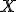 opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod
opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod 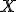 spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
Definícia.
Kružnica, ktorá sa dotýka všetkých strán daného trojuholníka sa nazýva vpísaná kružnica.
Vlastnosti
Definícia.
Kružnica, ktorá sa zvonka dotýka strany trojuholníka a dvoch priamok, ktoré sú predĺžením zvyšných strán trojuholníka sa nazýva
kružnica pripísaná trojuholníku.
Vlastnosti
Veta (Veta o osi vnútorného uhla).
V každom trojuholníku platí, že os vnútorného uhla delí protiľahlú stranu v rovnakom pomere, ako je pomer dĺžok príslušných priľahlých strán.
Cvičenie.
- Vyhľadajte v Euklidových Základoch tvrdenia - Kniha I. T/34 a Kniha III, T/3.
- Vyhľadajte v literatúre iné dôkazy vety o ortocentre trojuholníka.