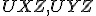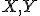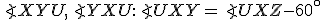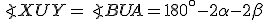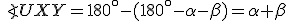Interaktívna geometria - planimetria
Geometria trojuholníka
Vybrané vety o trojuholníkoch
Definícia (Deliaci pomer).
Nech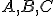 sú tri kolineárne body také, že
sú tri kolineárne body také, že 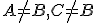 .
Deliaci pomer bodu
.
Deliaci pomer bodu  vzhľadom k bodom
vzhľadom k bodom 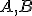 rozumieme reálne
číslo
rozumieme reálne
číslo 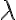 (označenie
(označenie 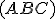 ), pre ktoré platí
), pre ktoré platí
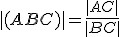 .
.
Pre bod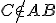 je
je 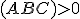 a pre bod
a pre bod 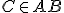 je
je 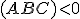 . Pre
. Pre 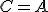 je zrejme
je zrejme 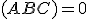 .
.
Nech
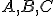 sú tri kolineárne body také, že
sú tri kolineárne body také, že 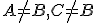 .
Deliaci pomer bodu
.
Deliaci pomer bodu  vzhľadom k bodom
vzhľadom k bodom 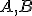 rozumieme reálne
číslo
rozumieme reálne
číslo 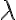 (označenie
(označenie 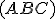 ), pre ktoré platí
), pre ktoré platí
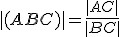 .
.Pre bod
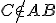 je
je 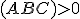 a pre bod
a pre bod 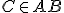 je
je 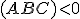 . Pre
. Pre 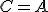 je zrejme
je zrejme 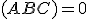 .
.
Poznámky.
- V niektorej literatúre sa pod deliacim pomerom troch rôznych kolineárnych bodov rozumie reálne číslo
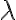 , pre ktoré platí:
, pre ktoré platí:
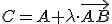 .
.
Takúto definíciu používa aj GeoGebra. - Deliaci pomer stredu úsečky je rovný -1. Dokážte to.
- Pre tri rôzne kolineárne body platí:
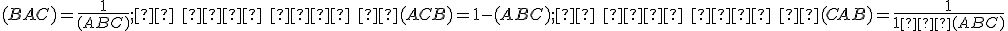 .
.
Dokážte to. - V rovine sú dané dva pevne body
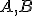 . Množina všetkých bodov
. Množina všetkých bodov 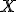 tejto roviny, pre ktoré platí
tejto roviny, pre ktoré platí
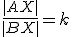 ,
,
kde je reálna konštanta, je kružnica. Dokážte to a vytvorte konštrukciu v GeoGebre.
je reálna konštanta, je kružnica. Dokážte to a vytvorte konštrukciu v GeoGebre.
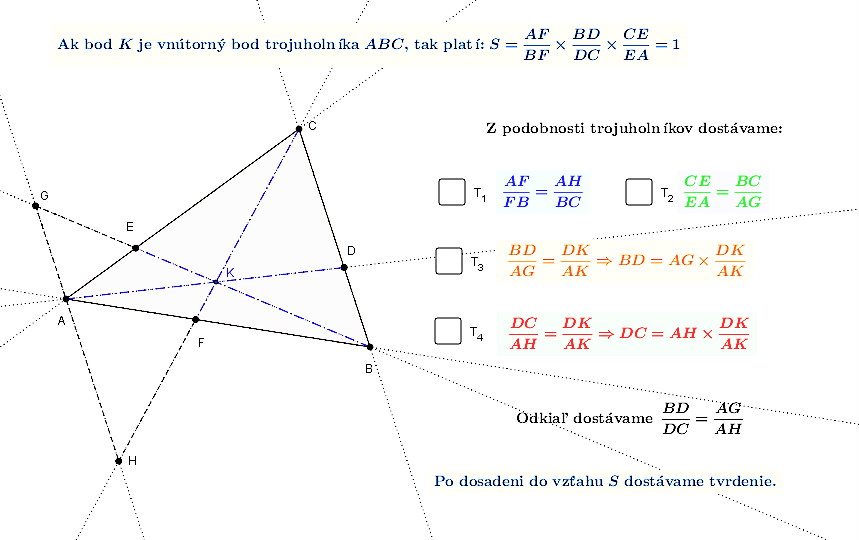
Cevova veta.
V trojuholníku sa priamky
sa priamky 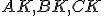 , kde
, kde 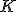 je vnútorným bodom trojuholníka
je vnútorným bodom trojuholníka  a
a
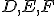 sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
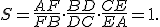
V trojuholníku
 sa priamky
sa priamky 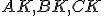 , kde
, kde 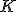 je vnútorným bodom trojuholníka
je vnútorným bodom trojuholníka  a
a
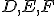 sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
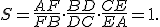
Giovanni Ceva bol taliansky matematik žijúci na prelome 17. a 18. storočia. Cevova veta stanovuje podmienku, kedy majú tri priamky prochádzajúce vrcholmi trojuholníka spoločný bod. Uvedieme jej prvú časť dôkazu, ktorý má konštrukčný charakter.
Dôkaz.
1. (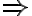 ): Ak sa priamky pretínajú v jednom bode, tak
): Ak sa priamky pretínajú v jednom bode, tak 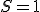 .
.
2. (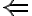 ): Ak
): Ak 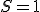 , tak sa priamky pretínajú v jednom bode.
, tak sa priamky pretínajú v jednom bode.
Pri dôkaze tejto implikácie sa vychádza z priesečníka dvoch priamok. Potom sa zostrojí priamka prechádzajúca týmto priesečníkom a tretím vrcholom. Následne sa dokáže, že táto priamka pretína protiľahlú stranu v bode, ktorý spĺňa podmienky vo vete. V dôkaze sa používajú tie isté podobnosti trojuholníkov ako v prvej časti dôkazu. Podrobnejší dôkaz nájdete v práci [Val, 2005].
Dôkaz.
1. (
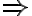 ): Ak sa priamky pretínajú v jednom bode, tak
): Ak sa priamky pretínajú v jednom bode, tak 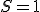 .
.
2. (
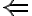 ): Ak
): Ak 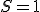 , tak sa priamky pretínajú v jednom bode.
, tak sa priamky pretínajú v jednom bode.
Pri dôkaze tejto implikácie sa vychádza z priesečníka dvoch priamok. Potom sa zostrojí priamka prechádzajúca týmto priesečníkom a tretím vrcholom. Následne sa dokáže, že táto priamka pretína protiľahlú stranu v bode, ktorý spĺňa podmienky vo vete. V dôkaze sa používajú tie isté podobnosti trojuholníkov ako v prvej časti dôkazu. Podrobnejší dôkaz nájdete v práci [Val, 2005].
Poznámky.
Aplikovaním Cévovej vety dokážte, že v ľubovoľnom trojuholníku sa:
Aplikovaním Cévovej vety dokážte, že v ľubovoľnom trojuholníku sa:
- Ťažnice sa pretínajú v jednom bode - ťažisku. (Využite skutočnosť, že ťažnice prechádzajú stredmi strán a každý z pomerov v Cévovej vete má tvar
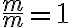 .)
.) - Výšky pretínajú v jednom bode - ortocentre. (Využite skutočnosť, že napr.
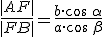 , ak
, ak 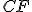 je výška.)
je výška.) - Osi vnútorných uhlov trojuholníka sa pretínajú v jednom bode - stred vpísanej kružnice. (Využite skutočnosť, že os vnútorného uhla rozdeľuje protiľahlú stranu na dve časti, ktorých dĺžky sú v rovnakom pomere ako im priľahlé strany trojuholníka.)
- Neskôr tieto tvrdenia dokážeme euklidovskou metódou.
Morleyho veta.
Ak v trojuholníku zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka
zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka 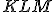 .
.
Ak v trojuholníku
 zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka
zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka 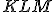 .
.
Morleyho veta predstavuje jednu z najprekvapujúcejších vlastností elementárnej geometrie, ktorú v roku 1899 objavil a dokázal anglo-americký matematik Frank Morley (1860-1937). Niektorí matematici nazývajú túto vetu aj ako Morleyov zázrak.
Poznámky.
- V 2. kroku dôkazu zhodnosť vyplýva z vety
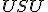 (uhly pri vrchole
(uhly pri vrchole 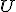 ... os uhla, pri vrchole
... os uhla, pri vrchole 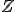 majú veľkosť
majú veľkosť 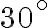 , strana
, strana 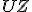 spoločná).
spoločná). - V 5. kroku dôkazu je potrebné ukázať, že trojuholník
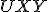 je rovnoramenný (uhly pri základni sú zhodné):
je rovnoramenný (uhly pri základni sú zhodné):
- Morleyova veta sa dá dokázať trigonometricky pomocou sínusovej a kosínusovej vety a vzorcov pre sčítanie uhlov.