Interaktívna geometria - planimetria
Neeuklidovská geometria
Hyperbolická priamka
Pokračovanie dôkazu tvrdenia o priemete h-priamky, v ktorom využijeme tvrdenie o mocnosti bodu ku kružnici.
Tvrdenie
Priemetom h-priamky (hyperboly) do Poincarè disku je otvorený kružnicový oblúk, ktorý je kolmý na hranicu kruhu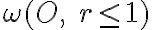 .
.
Pri dôkaze budeme potrebovať aj pojem dvojice inverzných bodov a pojem polárneho prvku v kruhovej inverzii. Viac o kruhovej inverzii nájdete v kurze Planimetria a stereometria
Tu. Najskôr dokážeme lemu:
Priemetom h-priamky (hyperboly) do Poincarè disku je otvorený kružnicový oblúk, ktorý je kolmý na hranicu kruhu
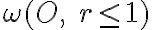 .
.
Lema
Nech je daná kruhová inverzia určená kružnicou - hranicou kruhu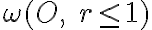 a nech bod
a nech bod 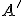 je obrazom bodu
je obrazom bodu 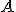 v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu
v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu  prechádzajúcu dvojicou inverzných bodov
prechádzajúcu dvojicou inverzných bodov 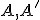 . Ak kružnica
. Ak kružnica  pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu
pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu 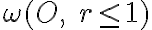 , tak kružnica
, tak kružnica  pretína kružnicu - hranicu kruhu
pretína kružnicu - hranicu kruhu 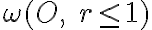 kolmo.
kolmo.
Nech je daná kruhová inverzia určená kružnicou - hranicou kruhu
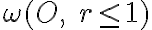 a nech bod
a nech bod 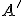 je obrazom bodu
je obrazom bodu 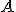 v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu
v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu  prechádzajúcu dvojicou inverzných bodov
prechádzajúcu dvojicou inverzných bodov 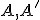 . Ak kružnica
. Ak kružnica  pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu
pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu 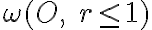 , tak kružnica
, tak kružnica  pretína kružnicu - hranicu kruhu
pretína kružnicu - hranicu kruhu 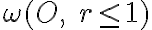 kolmo.
kolmo.
Dôkaz
V dôsledku lemy a predchádzajúcich častí dôkazu môžeme vysloviť tvrdenie.
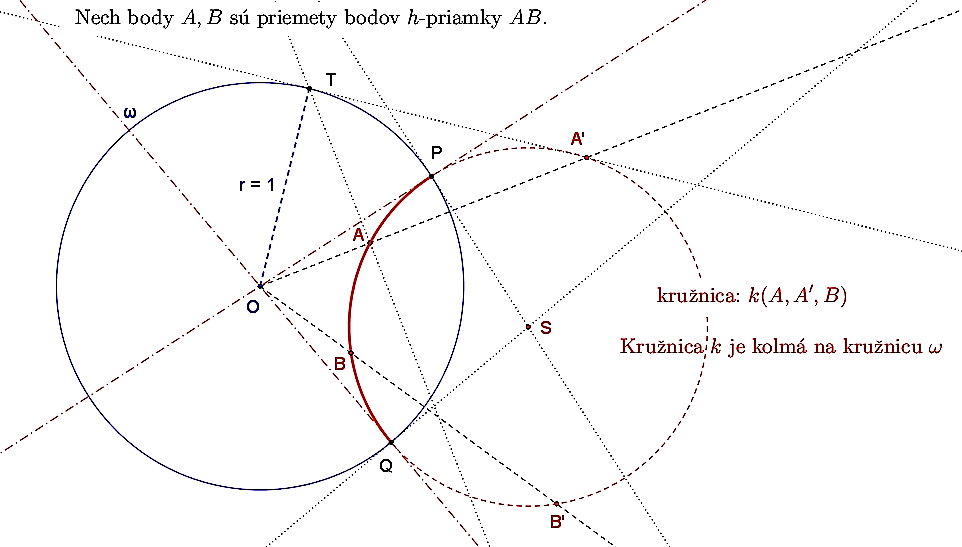
- Nech body
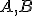 sú priemety bodov h-priamky
sú priemety bodov h-priamky 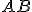 . Pozrite si priložený obrázok.
. Pozrite si priložený obrázok. - Podľa predchádzajúcej časti dôkazu (i.) platí
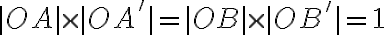 .
. - Odkiaľ: bod
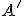 je obrazom bodu
je obrazom bodu 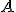 aj v kruhovej inverzii
aj v kruhovej inverzii 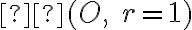 . Podobne to môžeme povedať aj o bodoch
. Podobne to môžeme povedať aj o bodoch 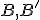 .
. - Nech
 je kružnica určená bodmi
je kružnica určená bodmi 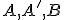 , potom v dôsledku mocnosti bodu
, potom v dôsledku mocnosti bodu 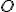 ku kružnici
ku kružnici  bude aj bod
bude aj bod 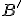 bodom kružnice
bodom kružnice  .
. - Teraz uvažujme o dotykových bodoch
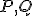 na dotyčniciach z bodu
na dotyčniciach z bodu 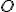 ku kružnici
ku kružnici  .
. - Mocnosť bodov
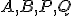 ku kružnici
ku kružnici 
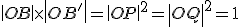
- Z toho vyplýva, že body
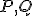 sú samodružné v kruhovej inverzii
sú samodružné v kruhovej inverzii 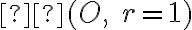 .
. - Priamky
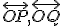 sú dotyčnice ku kružnici
sú dotyčnice ku kružnici  . Odkiaľ
. Odkiaľ 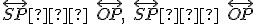 .
. - Kružnica
 je kolmá na kružnicu
je kolmá na kružnicu 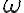 .
Tým je dôkaz lemy ukončený.
.
Tým je dôkaz lemy ukončený.
V dôsledku lemy a predchádzajúcich častí dôkazu môžeme vysloviť tvrdenie.
Poincarè diskový model (tiež sa používa označenie
Poincarè Disc) hyperbolickej roviny je prezentovaný v euklidovskej rovine ako
otvorený kruh
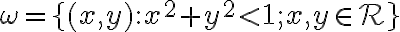 . Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
. Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
V predchádzajúcej časti sme uviedli, že tento otvorený kruh je stredovým priemetom dvojdielneho hyperboloidu. Uviedli sme tvrdenie, že v Poincarè diskovom modeli pre hyperbolické body a hyperbolické priamky platí:
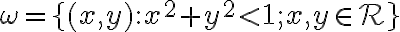 . Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
. Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
V predchádzajúcej časti sme uviedli, že tento otvorený kruh je stredovým priemetom dvojdielneho hyperboloidu. Uviedli sme tvrdenie, že v Poincarè diskovom modeli pre hyperbolické body a hyperbolické priamky platí:
- vlastný bod je vnútorný bod kruhu, ktorý je priemetom vlastného h-bodu hyperboloidu;
- koncový bod (resp. nevlastný bod) ležiaci na hranici kruhu, ktorý je priemetom nevlastného bodu 1. druhu;
- priamka je otvorený kružnicový oblúk kruhu - je priemetom h-priamky (hyperboly), pričom tento oblúk leží na kružnici kolmej na hranicu kruhu
Pri zostrojovaní hyperbolickej priamky určenej dvoma bodmi kruhu s výhodou využijeme vlastnosti kruhovej inverzie a konštrukcie popísané v predchádzajúcom dôkaze.
Poznámky
- V ďalšej podkapitole navrhneme v prostredí GeoGebra konštrukciu a zároveň aj nástroj na zostrojenie hyperbolickej priamky určenej dvoma rôznymi bodmi v Poincarè modeli disku. V konštrukcii využijeme inverzné body.
- Pri riešení konštrukčných úloh v Poincarè modeli potrebujeme okrem konštrukcie hyperbolickej priamky potrebovať aj konštrukciu kružnice a ďalších základných euklidovských konštrukcií (kolmica, os úsečky a pod).