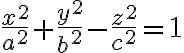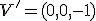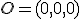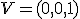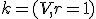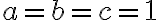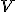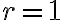Interaktívna geometria - planimetria
Neeuklidovská geometria
Modely
Poincarè model
Tvrdenie
Dôkaz
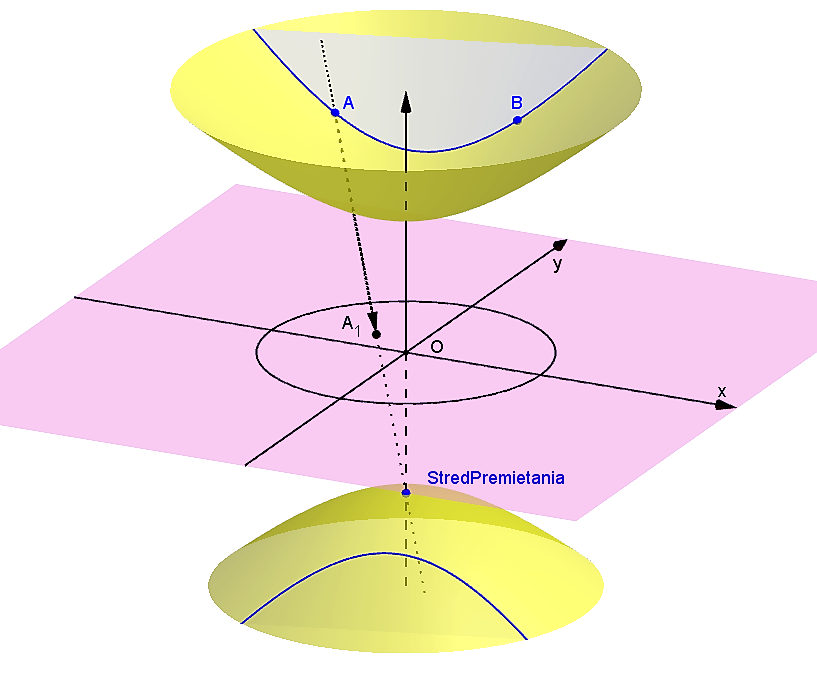
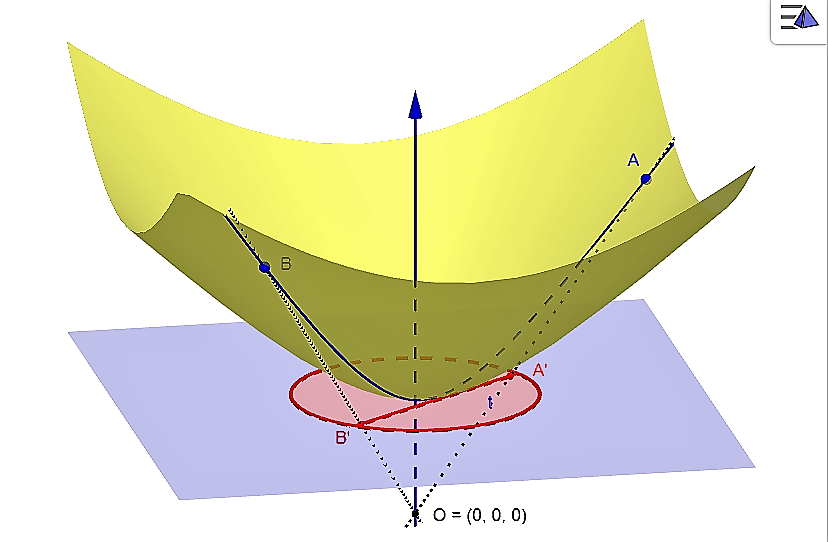
- Dôkaz prvej časti tohto tvrdenia vyplýva z vlastností stredového premietania, v ktorom sa kužeľová plocha obaľujúca hyperboloid zobrazí do kružnice
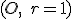 . To znamená, že ľubovoľný bod hyperboloidu sa zobrazí do vnútra kruhu
. To znamená, že ľubovoľný bod hyperboloidu sa zobrazí do vnútra kruhu 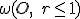 .
. - Dôkaz druhej časti o priemete h-priamky (reálne stredovej hyperboly) rozdelíme na dve etapy i. a ii.
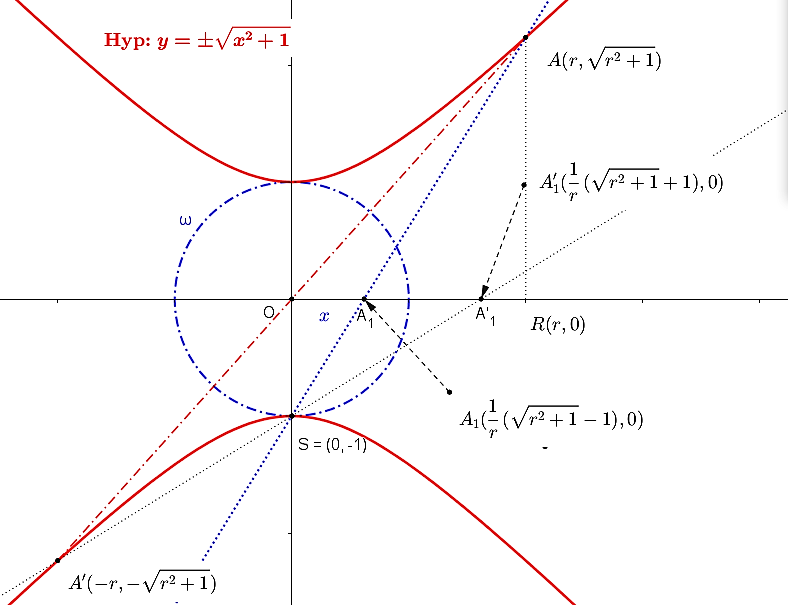
- Nech
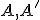 je dvojica združených bodov hyperboloidu a nech
je dvojica združených bodov hyperboloidu a nech 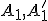 sú ich stredové priemety. Pre súčin vzdialeností
sú ich stredové priemety. Pre súčin vzdialeností
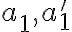 bodov
bodov 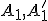 od stredu
od stredu  hyperboloidu platí:
hyperboloidu platí:
![a_1 \times a'_1=[ \frac{1}{r}(\sqrt{r^2+1}-1)] \times [\frac{1}{r}(\sqrt{r^2+1}+1)]=1 a_1 \times a'_1=[ \frac{1}{r}(\sqrt{r^2+1}-1)] \times [\frac{1}{r}(\sqrt{r^2+1}+1)]=1](https://lms.umb.sk/filter/tex/pix.php/bd6f2c6a62689c2e552273cc589b6f51.png) .
.
Dôkaz toho, že súčin vzdialeností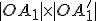 je konštantný je prezentovaný v nižšie priloženom applete.
je konštantný je prezentovaný v nižšie priloženom applete.
- Musíme ešte dokázať, že priemety h-bodov
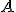 h-priamky (hyperboly) v označení
h-priamky (hyperboly) v označení 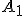 ležia na kružnici kolmej na kružnicu
ležia na kružnici kolmej na kružnicu 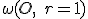 . Dôkaz je v ďalšej kapitole tejto práce. Pri dôkaze budeme potrebovať tvrdenie o mocnosti bodu ku kružnici.
. Dôkaz je v ďalšej kapitole tejto práce. Pri dôkaze budeme potrebovať tvrdenie o mocnosti bodu ku kružnici.
- Nech
Mocnosť bodu ku kružnici
Je daná kružnica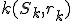 a bod
a bod  , ležiaci zvonka kružnice. Nech
, ležiaci zvonka kružnice. Nech  je sečnica kružnice
je sečnica kružnice  vedená bodom
vedená bodom  a
nech
a
nech 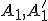 sú priesečníky sečnice
sú priesečníky sečnice  s kružnicou
s kružnicou 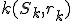 .
Pod mocnosťou bodu
.
Pod mocnosťou bodu  ku kružnici
ku kružnici 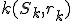 rozumieme číslo
rozumieme číslo 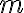 , pre ktoré platí:
, pre ktoré platí: 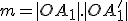 .
.
Je daná kružnica
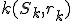 a bod
a bod  , ležiaci zvonka kružnice. Nech
, ležiaci zvonka kružnice. Nech  je sečnica kružnice
je sečnica kružnice  vedená bodom
vedená bodom  a
nech
a
nech 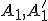 sú priesečníky sečnice
sú priesečníky sečnice  s kružnicou
s kružnicou 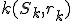 .
Pod mocnosťou bodu
.
Pod mocnosťou bodu  ku kružnici
ku kružnici 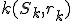 rozumieme číslo
rozumieme číslo 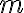 , pre ktoré platí:
, pre ktoré platí: 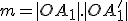 .
.
Viac o mocnosti bodu ku kružnice nájdete v kurze Planimetria a stereometria Tu. Vlastnosť mocnosť stačí vhodne aplikovať na náš prípad. Ilustráciu tvrdenia o priemete h-priamky prezentuje nasledujúci applete. Podrobný dôkaz (časti ii.) nájde čitateľ v ďalšej podkapitole s názvom "Hyperbolická priamka". Pozrite si tiež kapitolu "The Poincaré Disk Model" v práci [HIT].
Beltramiho-Kleinov model
Model vznikne ako stredový priemet dvojdielneho hyperboloidu do roviny kolmej na os hyperboloidu, pričom
Model vznikne ako stredový priemet dvojdielneho hyperboloidu do roviny kolmej na os hyperboloidu, pričom
Zhrnutie
- Bodmi Beltrami Kleinovho modelu sú body Klein Disku.
- Priamkami sú tetivy tohto disku.
V obidvoch hyperbolických modeloch (Beltrami a Poincarè) neplatí axióma rovnobežnosti.
- V obidvoch prípadoch existuje viac ako jedna rovnobežka.
- Existencia rovnobežky vyplýva z prvých skupín axióm.
- V modeli "Sféra" nemáme zaručenú ani existenciu rovnobežky.
- Kleinov disk a Poincarè disk sú modely, ktoré vzniknú aj premietaním do vhodnej roviny. Pozri Disk a hyperboloid.
- Výhodou modelu Klein je, že priamky v tomto modeli sú euklidovské (rovné) tetivy. Nevýhodou je, že model nie je konformný (kruhy a uhly sú skreslené).
- Neeuklidovská hyperbolická geometria reprezentovaná Poincarè diskom je konformná.