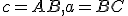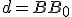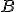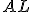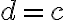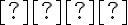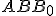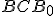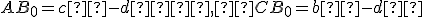Interaktívna geometria - planimetria
Euklidove Základy
Euklidovské konštrukcie
Ako sme už uviedli, pri dokazovaní mnohých tvrdení týkajúcich sa vlastností geometrických útvarov, Euklides využíva hlavne konštrukčnú metódu. Pri podrobnejšom skúmaní týchto konštrukčných dôkazov zistíme, že navrhnuté konštrukcie sa dajú vo väčšine prípadov realizovať len použitím pravítka a kružidla. V odbornej literatúre sa takéto konštrukcie nazývajú euklidovské.
Definícia.
Grafická konštrukcia v euklidovskej rovine (alebo v euklidovskom priestore) realizovaná len
Grafická konštrukcia v euklidovskej rovine (alebo v euklidovskom priestore) realizovaná len
- ideálnym pravítkom a ideálnym kružidlom
- a konečným počtom krokov sa nazýva Euklidovská konštrukcia.
Každý krok elementárnej konštrukcie predstavuje zostrojenie
- priamky prechádzajúcej dvoma danými rôznymi bodmi alebo
- kružnice so stredom v danom bode a s daným polomerom alebo
- priesečníka dvoch rôznobežných priamok (resp. prieniku priamky a kružnice alebo prieniku dvoch kružníc).
Elementárne euklidovské konštrukcie
- Zostrojenie rovnostranného trojuholníka. Kniha 1, Tvrdenie I.
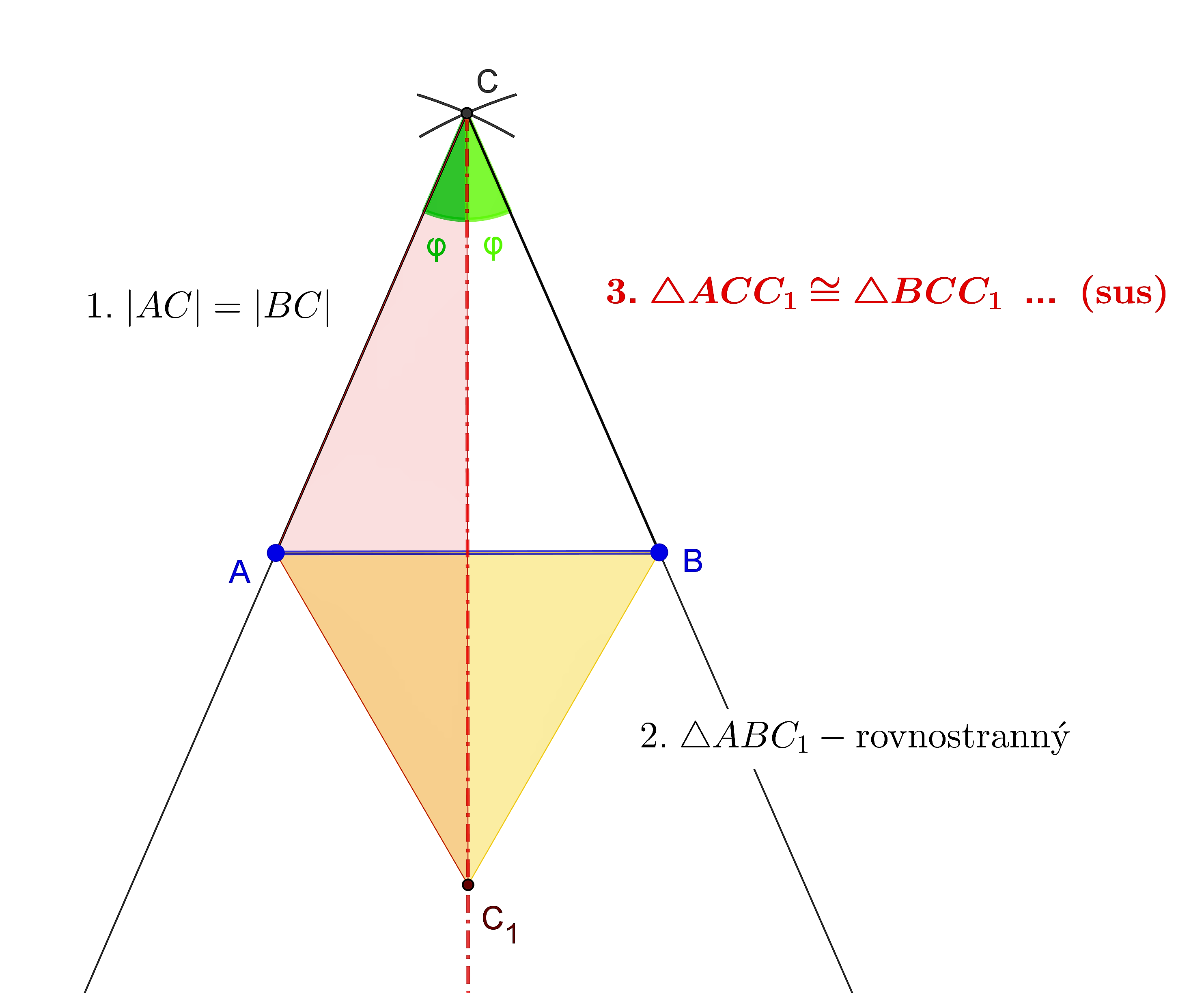
- Zostrojenie osi daného uhla. Kniha 1, Tvrdenie IX.
- Zostrojenie stredu danej úsečky. Kniha 1, Tvrdenie X.
- Zostrojenie osi úsečky.
- Zostrojenie kolmice v danom bode na danú priamku. Kniha 1, Tvrdenie XI. Mezi elementárne euklidovské konštrukcie zaraďujeme aj konštrukcie používané v školskej matematike už na 1. stupni ZŠ
- "Prenesenie" danej úsečky na danú polpriamku. Kniha 1, Tvrdenie II a III.
- "Prenesenie" daného uhla na danú polpriamku v danej polrovine.
Poznámky.
- Podmienka konečného počtu krokov v definícii euklidovskej konštrukcii je opodstatnená. Napríklad konštrukcia uvedená v príklade v kapitole 2 nemôže byť euklidovská, lebo pri konečnom počte aproximácií nezískame trisekciu uhla. Na druhej strane vieme stanoviť počet krokov, ktoré budú veľkosť trisekcie uhla určovať s vopred danou presnosťou .
- Prvé tri uvedené elementárne konštrukcie nie je problém zrealizovať, ak máme k dispozícii pravítko a kružidlo. Pozrite si napríklad konštrukciu osi uhla a osi úsečky (úloha č. 4).
- V geometrii, v ktorej neplatí piaty Euklidov postulát (neeuklidovské geometrie) to také jednoduché nebude. V prvom rade musíme nájsť odpoveď na otázku: "Čo budeme rozumieť pod pravítkom resp. kružidlom v takejto geometrii?"
- V časti Neeuklidovská geometria popíšeme niektoré elementárne euklidovské konštrukcie v neeuklidovskej geometrii, ktoré budú tvoriť samostatnú triedu Euklidovských konštrukcií.
Podľa prof. Šedivého euklidovská konštrukcia sa považuje za zrealizovanú ak sú splnené podmienky K1 až
K6.
K1: Bod je zostrojený, ak je daná jeho poloha, alebo je priesečníkom dvoch priamok, dvoch kružníc alebo priamky a kružnice.
K2: Priamku považujeme za zostrojenú, ak sú dané jej dva rôzne body.
K3: Kružnicu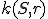 považujeme za zostrojenú, ak je daný bod
považujeme za zostrojenú, ak je daný bod  a úsečka
a úsečka  .
.
K4: Ak sú dané dve rôznobežky , potom považujeme ich priesečník
, potom považujeme ich priesečník 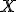 za zostrojený.
za zostrojený.
K5: Ak je daná kružnica a jej sečnica, potom považujeme ich priesečníky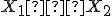 za zostrojené.
za zostrojené.
K6: Ak sú dané dve kružnice, o ktorých vieme, že sa pretínajú, potom považujeme ich priesečníky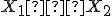 za zostrojené.
za zostrojené.
Základné euklidovské konštrukcie môžeme považovať za elementárne stavebné kroky pri zostrojovaní zložitejších geometrických útvarov, pre ktorý sú dané nutné "generujúce" prvky.
Napríklad zostrojiť trojuholník, ak sú dané dve jeho strany a uhol nimi zovretý, je možné zrealizovať na základe vety sus o zhodnosti trojuholníkov [Kniha 1, Tvrdenie IV].
K1: Bod je zostrojený, ak je daná jeho poloha, alebo je priesečníkom dvoch priamok, dvoch kružníc alebo priamky a kružnice.
K2: Priamku považujeme za zostrojenú, ak sú dané jej dva rôzne body.
K3: Kružnicu
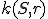 považujeme za zostrojenú, ak je daný bod
považujeme za zostrojenú, ak je daný bod  a úsečka
a úsečka  .
.
K4: Ak sú dané dve rôznobežky
 , potom považujeme ich priesečník
, potom považujeme ich priesečník 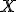 za zostrojený.
za zostrojený.
K5: Ak je daná kružnica a jej sečnica, potom považujeme ich priesečníky
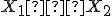 za zostrojené.
za zostrojené.
K6: Ak sú dané dve kružnice, o ktorých vieme, že sa pretínajú, potom považujeme ich priesečníky
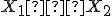 za zostrojené.
za zostrojené.
Základné euklidovské konštrukcie môžeme považovať za elementárne stavebné kroky pri zostrojovaní zložitejších geometrických útvarov, pre ktorý sú dané nutné "generujúce" prvky.
Napríklad zostrojiť trojuholník, ak sú dané dve jeho strany a uhol nimi zovretý, je možné zrealizovať na základe vety sus o zhodnosti trojuholníkov [Kniha 1, Tvrdenie IV].
Definícia (konštrukčná úloha).
Zostrojenie (konštrukciu) geometrického útvaru z daných prvkov sa nazýva konštrukčná úloha.
Zostrojenie (konštrukciu) geometrického útvaru z daných prvkov sa nazýva konštrukčná úloha.
Riešiť konštrukčnú úlohu znamená:
- odvodiť vzťahy medzi zadanými a hľadanými prvkami - náčrtok, rozbor,
- konštrukčne doplniť zadané prvky ďalšími tak, aby bol útvar zostrojiteľný - postup konštrukcie a jeho grafické prevedenie - konštrukcia,
- urobiť dôkaz, že zostrojený útvar je ten, ktorý bolo treba zostrojiť - dôkaz správnosti konštrukcie,
- stanoviť, za ktorých podmienok je úloha riešiteľná a prípadne koľko má vyhovujúcich riešení - diskusia.
Rozbor - prvá etapa riešenia konštrukčnej úlohy, metóda: geometrické miesto bodov. V rozbore ide o hľadanie kauzalít medzi
danými 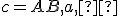 a hľadanými prvkami geometrického útvaru
a hľadanými prvkami geometrického útvaru  .
.
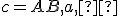 a hľadanými prvkami geometrického útvaru
a hľadanými prvkami geometrického útvaru  .
.
Záver analýzy
Z rozboru vyplýva postup konštrukcie trojuholníka : strana
: strana 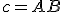 ; uhol
; uhol
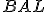 ; kružnica
; kružnica 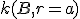 ... vrchol
... vrchol  je priesečník ramena uhla
a kružnice.
je priesečník ramena uhla
a kružnice.
Z rozboru vyplýva postup konštrukcie trojuholníka
 : strana
: strana 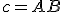 ; uhol
; uhol
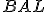 ; kružnica
; kružnica 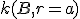 ... vrchol
... vrchol  je priesečník ramena uhla
a kružnice.
je priesečník ramena uhla
a kružnice.
Konštrukcia - druhá etapa riešenia konštrukčnej úlohy
Konštrukcia sa skladá z dvoch častí: grafická konštrukcia (narysovanie hľadaného útvaru) a zápis krokov (robí sa vedľa). Stiahnite si applet Tu.
Konštrukcia sa skladá z dvoch častí: grafická konštrukcia (narysovanie hľadaného útvaru) a zápis krokov (robí sa vedľa). Stiahnite si applet Tu.
Dôkaz - tretia etapa riešenia konštrukčnej úlohy. Dôkazom sa chápe argumentácia, či útvar vytvorený konštrukciou spĺňa všetky požiadavky uvedené v zadaní úlohy. V našom príklade dôkaz vyplýva z postupu konštrukcie.
Diskusia - štvrtá etapa riešenia konštrukčnej úlohy
Nech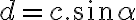 je vzdialenosť bodu
je vzdialenosť bodu  od priamky
od priamky 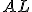 , potom počet priesečníkov
, potom počet priesečníkov
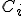 závisí na hodnotách
závisí na hodnotách 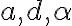 . Musíme rozlíšiť dve základné situácie:
. Musíme rozlíšiť dve základné situácie:
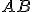 existujú dva uhly
existujú dva uhly 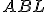 a
a 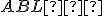 veľkosti
veľkosti  , čo zdvojnásobuje počet riešení. Sú však osovo symetrické.
, čo zdvojnásobuje počet riešení. Sú však osovo symetrické.
- V diskusii určujeme za akých podmienok je úloha riešiteľná, prípadne určujeme koľko má vyhovujúcich riešení resp. skúmame závislosť riešenia od zadaných prvkov.
- V tejto úlohe výhodne vyžijeme posuvníky a počet riešení odvodíme od vzájomnej polohy daných prvkov.
Nech
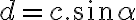 je vzdialenosť bodu
je vzdialenosť bodu  od priamky
od priamky 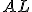 , potom počet priesečníkov
, potom počet priesečníkov
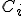 závisí na hodnotách
závisí na hodnotách 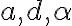 . Musíme rozlíšiť dve základné situácie:
. Musíme rozlíšiť dve základné situácie:
- Pokiaľ platí, že
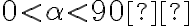 , potom je
, potom je 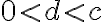 a úloha
a úloha
a) nemá riešenie, ak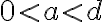
b) má práve jedno riešenie pre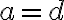 alebo
alebo
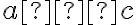
c) má práve dve riešenia za podmienky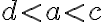 .
.
- Pre
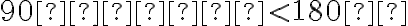 je diskusia jednoduchšia, úloha
je diskusia jednoduchšia, úloha
a) nemá riešenie za podmienky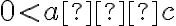
b) má práve jedno riešenie, pokiaľ platí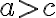 .
.
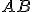 existujú dva uhly
existujú dva uhly 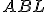 a
a 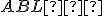 veľkosti
veľkosti  , čo zdvojnásobuje počet riešení. Sú však osovo symetrické.
, čo zdvojnásobuje počet riešení. Sú však osovo symetrické.