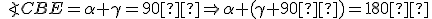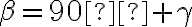Interaktívna geometria - planimetria
Euklidove Základy
Rovnoramenný trojuholník
Euklidove definície (Servít: "Výmery")
Definícia 20
Z trojstranných útvarov je trojuholník:
Okrem toho z trojstranných útvarov je trojuholník:
Z trojstranných útvarov je trojuholník:
- rovnostranný, ktorý má tri strany rovnaké;
- rovnoramenný, ktorý má len dve strany rovnaké;
- rôznostranný, ktorý má tri strany nerovnaké.
Okrem toho z trojstranných útvarov je trojuholník:
- pravouhlý, ktorý má pravý uhol;
- tupouhlý, ktorý má tupý uhol;
- ostrouhlý majúci tri uhly ostré.
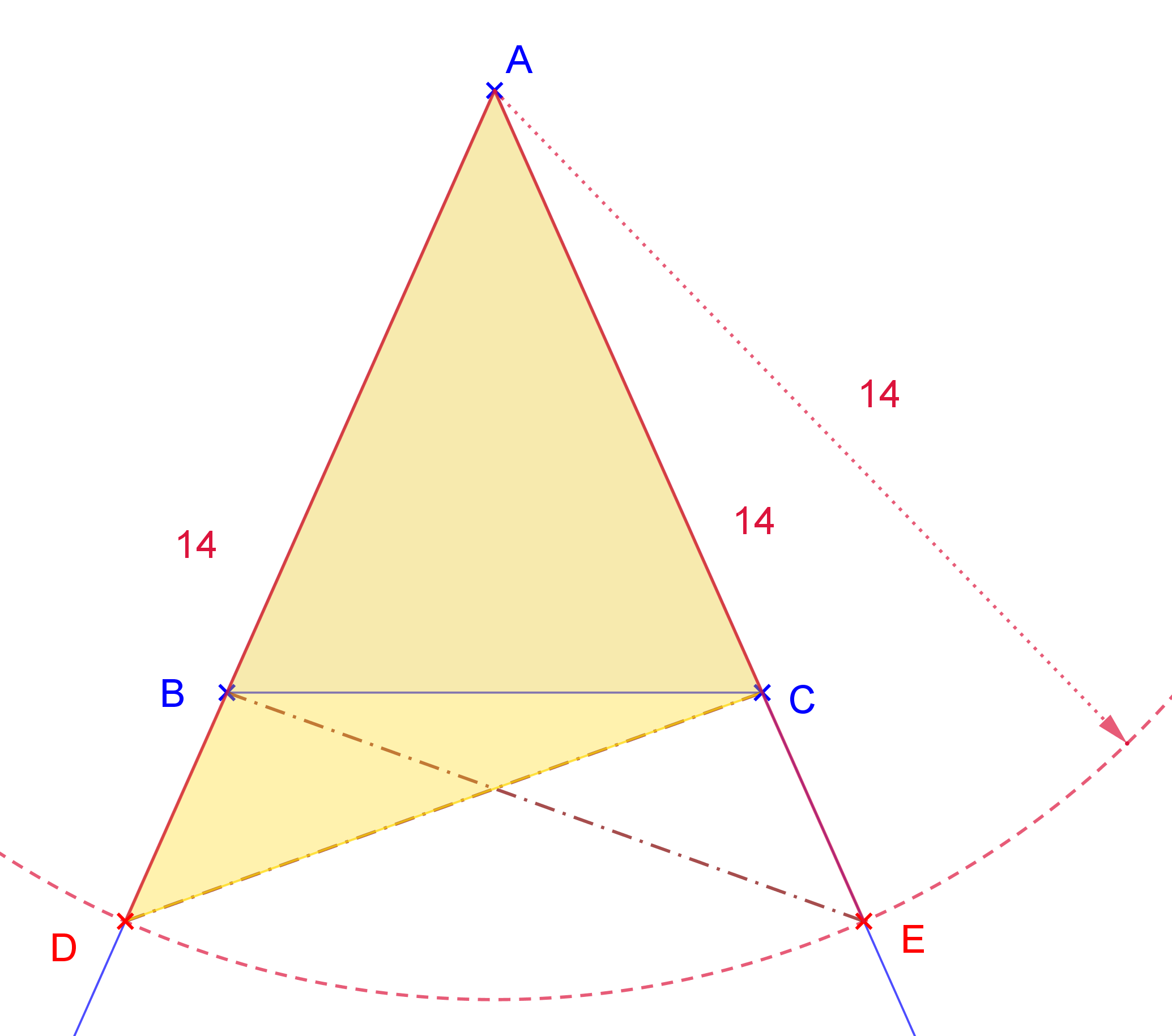
Jedným z fundamentálnych Euklidových tvrdení, ktoré sa využíva v dôkazoch mnohých ďalších tvrdení je veta o zhodnosti uhlov pri základni rovnoramenného trojuholníka. Dôkaz tohto tvrdenia je typicky konštrukčný a zásadne sa líši od bežne používaného dôkazu v stredoškolskej matematike. V dôkaze sa vytvoria dva nové a zároveň zhodné trojuholníky podľa vety (sus). V konštrukcii sa používa len pravítko a kružidlo.
Kniha 1, Tvrdenie V
V rovnoramenných trojuholníkoch sa uhly pri základni navzájom rovnajú; a ak sa predĺžia rovnaké priamky (ramená), uhly pod základňou navzájom rovnajú.
V rovnoramenných trojuholníkoch sa uhly pri základni navzájom rovnajú; a ak sa predĺžia rovnaké priamky (ramená), uhly pod základňou navzájom rovnajú.
Dôkaz
Veľmi poučný je aj dôkaz Tvrdenia XIII, ktorý je publikovaný v prvej knihe Základov. Toto tvrdenie zohráva významnú úlohu pri geometrii uhlov.
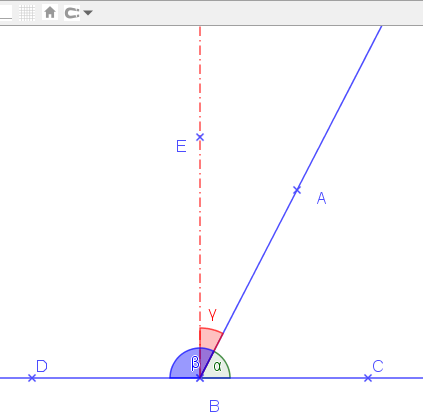
Kniha 1, Tvrdenie XIII
Ak priamka stojí na priamke, vytvára buď dva pravé uhly alebo uhly, ktorých súčet sa rovná dvom pravým uhlom.
Ak priamka stojí na priamke, vytvára buď dva pravé uhly alebo uhly, ktorých súčet sa rovná dvom pravým uhlom.
Dôkaz
Upravený podľa českého prekladu Euklidových Základov.
Nech akákoľvek priamka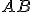 stojaca na priamke
stojaca na priamke 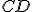 vytvára uhly
vytvára uhly 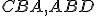 . Hovorím, že buď uhly
. Hovorím, že buď uhly 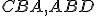 sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
Upravený podľa českého prekladu Euklidových Základov.
Nech akákoľvek priamka
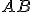 stojaca na priamke
stojaca na priamke 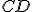 vytvára uhly
vytvára uhly 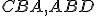 . Hovorím, že buď uhly
. Hovorím, že buď uhly 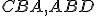 sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
sú dva pravé uhly alebo ich súčet sa rovná dvom pravým uhlom.
-
Ak sa teraz uhol
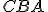 rovná uhlu
rovná uhlu 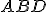 , potom sú to dva pravé uhly.
Def.10
, potom sú to dva pravé uhly.
Def.10
-
Ale ak nie, nakreslite
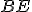 z bodu
z bodu 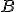 v pravom uhle k
v pravom uhle k 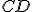 . Preto uhly
. Preto uhly 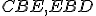 sú dva pravé uhly.
T/XI
sú dva pravé uhly.
T/XI
-
Pretože uhol
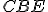 sa rovná súčtu dvoch uhlov
sa rovná súčtu dvoch uhlov 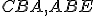 , pridajte uhol
, pridajte uhol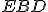 ku každému,
takže súčet uhlov
ku každému,
takže súčet uhlov 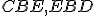 sa rovná súčtu troch uhlov
sa rovná súčtu troch uhlov 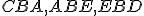 .
Z.2, Z.4
.
Z.2, Z.4
-
Pretože uhol
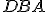 sa rovná súčtu dvoch uhlov
sa rovná súčtu dvoch uhlov 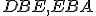 , ku každému z nich pridajte uhol
, ku každému z nich pridajte uhol 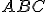 ,
preto sa súčet uhlov
,
preto sa súčet uhlov 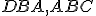 rovná súčtu troch uhlov
rovná súčtu troch uhlov 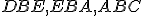 . Z.2, Z.5
. Z.2, Z.5
-
Ale súčet uhlov
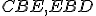 sa tiež ukázal byť rovný súčtu rovnakých troch uhlov a veci, ktoré sa rovnajú rovnakému,
sa rovnajú rovnako sebe, preto súčet uhlov
sa tiež ukázal byť rovný súčtu rovnakých troch uhlov a veci, ktoré sa rovnajú rovnakému,
sa rovnajú rovnako sebe, preto súčet uhlov 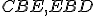 sa rovná súčtu uhlov
sa rovná súčtu uhlov 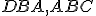 .
Uhly
.
Uhly 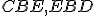 sú však dva pravé uhly, takže súčet uhlov
sú však dva pravé uhly, takže súčet uhlov 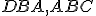 sa tiež rovná dvom pravým uhlom. Z.1, Z.6
sa tiež rovná dvom pravým uhlom. Z.1, Z.6
- Preto ak priama čiara stojí na priamke, vytvára buď dva pravé uhly alebo uhly, ktorých súčet sa rovná dvom pravým uhlom.