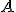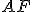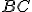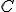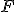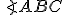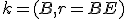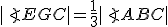Interaktívna geometria - planimetria
Euklidove Základy
“Pane, niet kráľovskej cesty ku geometrii.”
Euklidova odpoveď na žiadosť Ptolemaia I. vysvetliť mu svoje Základy rýchlo a ľahko.
Euklidova odpoveď na žiadosť Ptolemaia I. vysvetliť mu svoje Základy rýchlo a ľahko.
Základnými kameňmi pri axiomatickom budovaní geometrie sú
- Základné pojmy (Definície) Euklides popisuje intuitívne pomocou zaužívaných pojmov ako „dĺžka, šírka, ..." . Napr.:
- Bod je to, čo nemá dĺžku.
- Čiara je dĺžka bez šírky.
- Hranicami čiary sú body.
- Priamka (Euklides vo svojich Základoch pod pojmom priamka
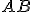 chápe úsečku
chápe úsečku 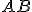 ) je čiara, ktorá je v každom svojom bode rovná.
) je čiara, ktorá je v každom svojom bode rovná. - Trojuholník ... (vyhľadajte definíciu
 v Euklidových Základoch).
v Euklidových Základoch). - V skutočnosti sa predpokladá, že čitateľ vie, čo si má pod týmito pojmami predstaviť. Celkove Euklides uvádza 23 definícií.
- Axiómy - postuláty, ktorých pravdivosť sa nespochybňuje.
- Odvodené pojmy (Zásady, Common notion) sa definujú pomocou základných pojmov a prijatých axióm.
- Tvrdenia (Proposition) sú dokazované pomocou základných pojmov, axióm a odvodených pojmov.
Euklides vo svojich Základoch uvádza len päť axióm:
Post 1: Nakresliť priamku z ľubovoľného bodu do ľubovoľného bodu.
Post 2: A priamku možno neohraničene na obe strany predĺžiť.
Post 3: A z akéhokoľvek bodu a akýmkoľvek polomerom možno narysovať kružnicu.
Post 4: A každé dva pravé uhly sú navzájom "zhodné".
Post 5: A keď priamka pretínajúca dve priamky tvorí s nimi na jednej strane vnútorné uhly menšie než dva pravé, pretnú sa tieto priamky neohraničene predĺžené na tej strane, kde súčet uhlov je menší než dva pravé.
Post 1: Nakresliť priamku z ľubovoľného bodu do ľubovoľného bodu.
Post 2: A priamku možno neohraničene na obe strany predĺžiť.
Post 3: A z akéhokoľvek bodu a akýmkoľvek polomerom možno narysovať kružnicu.
Post 4: A každé dva pravé uhly sú navzájom "zhodné".
Post 5: A keď priamka pretínajúca dve priamky tvorí s nimi na jednej strane vnútorné uhly menšie než dva pravé, pretnú sa tieto priamky neohraničene predĺžené na tej strane, kde súčet uhlov je menší než dva pravé.
Prvé tri postuláty majú konštrukčný charakter, pričom popisujú skúsenosť z rysovania pomocou pravítka a kružidla. Tieto postuláty umožňujú v (euklidovskej) rovine:
- narysovať priamku prechádzajúcu dvoma danými bodmi;
- ľubovoľne predĺžiť úsečku;
- narysovať kružnicu s daným stredom a polomerom.
- narysovať priamku prechádzajúcu dvoma danými bodmi;
- ľubovoľne predĺžiť úsečku;
- narysovať kružnicu s daným stredom a polomerom.
Piaty postulát so svojou nejasnou nezávislosťou od zvyšných postulátov má špecifické postavenie. Matematici sa asi 2000 rokov snažili piaty postulát dokázať z predchádzajúcich alebo ho aspoň nahradiť niečím jednoduchším, zjavnejším. Neúspešne
Za postulátmi nasledujú odvodené pojmy alebo zásady:
Za zásadami nasledujú tvrdenia. Prevažná väčšina tvrdení v Euklidových Základoch je dokazovaná prevažne formou konštrukcie resp. návodov ako postupovať pri dokazovaní týchto tvrdení. V ďalšej časti uvedieme niektoré tvrdenia z prvej knihy Základov.
- Ak sa dve rovnajú tretiemu, rovnajú sa aj navzájom.(Servít)
Veci, ktoré sa rovnajú tej istej veci, sa tiež navzájom rovnajú. (Preklad z angl. verzie.) - A ak sa rovným pridá rovné, sú aj celky rovné.
- A ak sa od rovných odnímu rovné, sú aj celky rovné.
- A útvary, ktoré sa (pohybom?) stotožňujú, sú navzájom rovné.
- A celok je väčší ako časť.
Za zásadami nasledujú tvrdenia. Prevažná väčšina tvrdení v Euklidových Základoch je dokazovaná prevažne formou konštrukcie resp. návodov ako postupovať pri dokazovaní týchto tvrdení. V ďalšej časti uvedieme niektoré tvrdenia z prvej knihy Základov.
Euklidove Základy - tvrdenia
Pri dokazovaní prvých dvoch tvrdení Euklides využíva postulát o konštruovateľnosti kružnice. Tiež používa definíciu
kruhu (Základy, Definícia 15), v ktorej predpokladá existenciu kruhu určeného stredom a polomerom. Definícia kruhu v Základoch má znenie:
Kruh je útvar rovinný ohraničený jednou čiarou (nazýva sa obvod resp. kružnica) tak, že všetky priamky (úsečky), ktoré vychádzajú z jedného bodu vo vnútri útvaru, sa navzájom rovnajú.
Definícia kruhu v Základoch intuitívne používa pojmy "medzi" a "zhodnosť", ktoré nie sú zavedené. Neskôr (takmer dve tisíc rokov) tieto pojmy zavádza Hilbert vo svojom axiomatickom systéme, kde sa kružnica po zavedení axióm zhodnosti už môže korektne zadefinovať.
Na záver tohto úvodného pohľadu na Euklidove Základy uvedieme "doslovný" preklad dôkazu Tvrdenia IV - (Základná veta o zhodnosti trojuholníkov 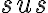 )
)
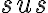 )
)
Kniha 1, Tvrdenie IV. Ak sa dva trojuholníky zhodujú v dvoch stranách a v uhle nimi určenom, tak sú zhodné.
Dôkaz .
-
Nech
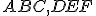 sú dva trojuholníky, ktoré majú dve strany
sú dva trojuholníky, ktoré majú dve strany 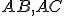 rovné dvom stranám
rovné dvom stranám 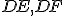 . Konkrétne
. Konkrétne 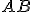 rovná
rovná
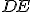 a
a 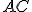 rovná
rovná 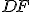 a uhol
a uhol 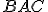 je rovný uhlu
je rovný uhlu 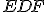 .
.
-
Hovorím (Euklides), že základňa
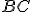 sa rovná aj základni
sa rovná aj základni 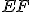 , trojuholník
, trojuholník  sa rovná trojuholníku
sa rovná trojuholníku 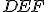 a zostávajúce uhly sa rovnajú zostávajúcim uhlom, respektíve opačne rovnakým stranám. To znamená, že uhol
a zostávajúce uhly sa rovnajú zostávajúcim uhlom, respektíve opačne rovnakým stranám. To znamená, že uhol  sa rovná uhlu
sa rovná uhlu 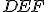 a uhol
a uhol 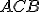 sa rovná uhlu
sa rovná uhlu 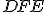 .
Nepriamy dôkaz
.
Nepriamy dôkaz
-
Nech trojuholník
 je uložený na trojuholníku
je uložený na trojuholníku 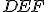 a ak je bod
a ak je bod  umiestnený na bode
umiestnený na bode 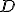 a priamka
a priamka 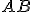 na
na 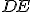 .
.
-
Priamka
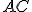 sa tiež rovná
sa tiež rovná 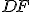 , pretože uhol
, pretože uhol 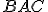 sa rovná uhlu
sa rovná uhlu 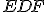 .
.
-
Ale
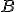 a tiež zhoduje s
a tiež zhoduje s 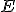 , a preto základňa
, a preto základňa 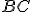 sa zhoduje so základňou
sa zhoduje so základňou 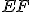 a rovná sa jej.
a rovná sa jej.
-
Takže celý trojuholník
 sa zhoduje s celým trojuholníkom
sa zhoduje s celým trojuholníkom 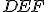 .
.
-
Zvyšné uhly sa zhodujú so zostávajúcimi uhlami a rovnajú sa, uhol
 sa rovná uhlu
sa rovná uhlu 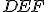 a uhol
a uhol 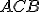 sa rovná uhlu
sa rovná uhlu 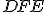 .
.
- Preto ak dva trojuholníky majú dve strany rovnobežné s dvoma stranami a majú uhly obsiahnuté rovnými čiarami rovnaké, potom majú aj základňu rovnú základni, trojuholník sa rovná trojuholníku a zvyšné uhly sú rovné zvyšným uhlom respektíve tým, ktoré sú oproti rovnakým stranám.
Komentár k dôkazu tvrdenia T/IV je prevzatý a upravený z Euklidových Základov podľa Servíta.
Poznámka
Pri dokazovaní tohto tvrdenia sa predpokladá, že pri prenášaní úsečky (T/II, T/III) resp. uhla sa ich veľkosť nezmení. Toto v Hilbertovej sústave zabezpečujú axiómy zhodnosti.
Pri dokazovaní tohto tvrdenia sa predpokladá, že pri prenášaní úsečky (T/II, T/III) resp. uhla sa ich veľkosť nezmení. Toto v Hilbertovej sústave zabezpečujú axiómy zhodnosti.
Riešenie
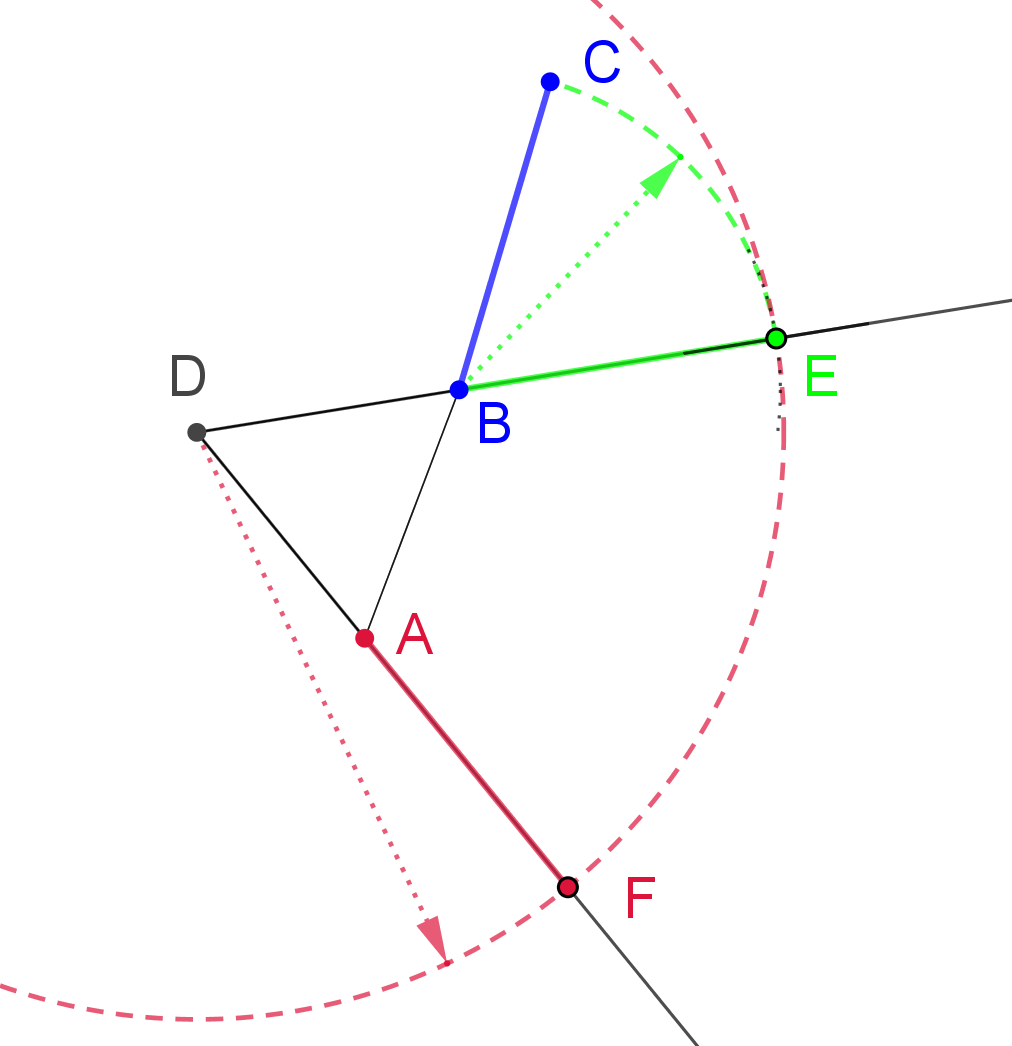
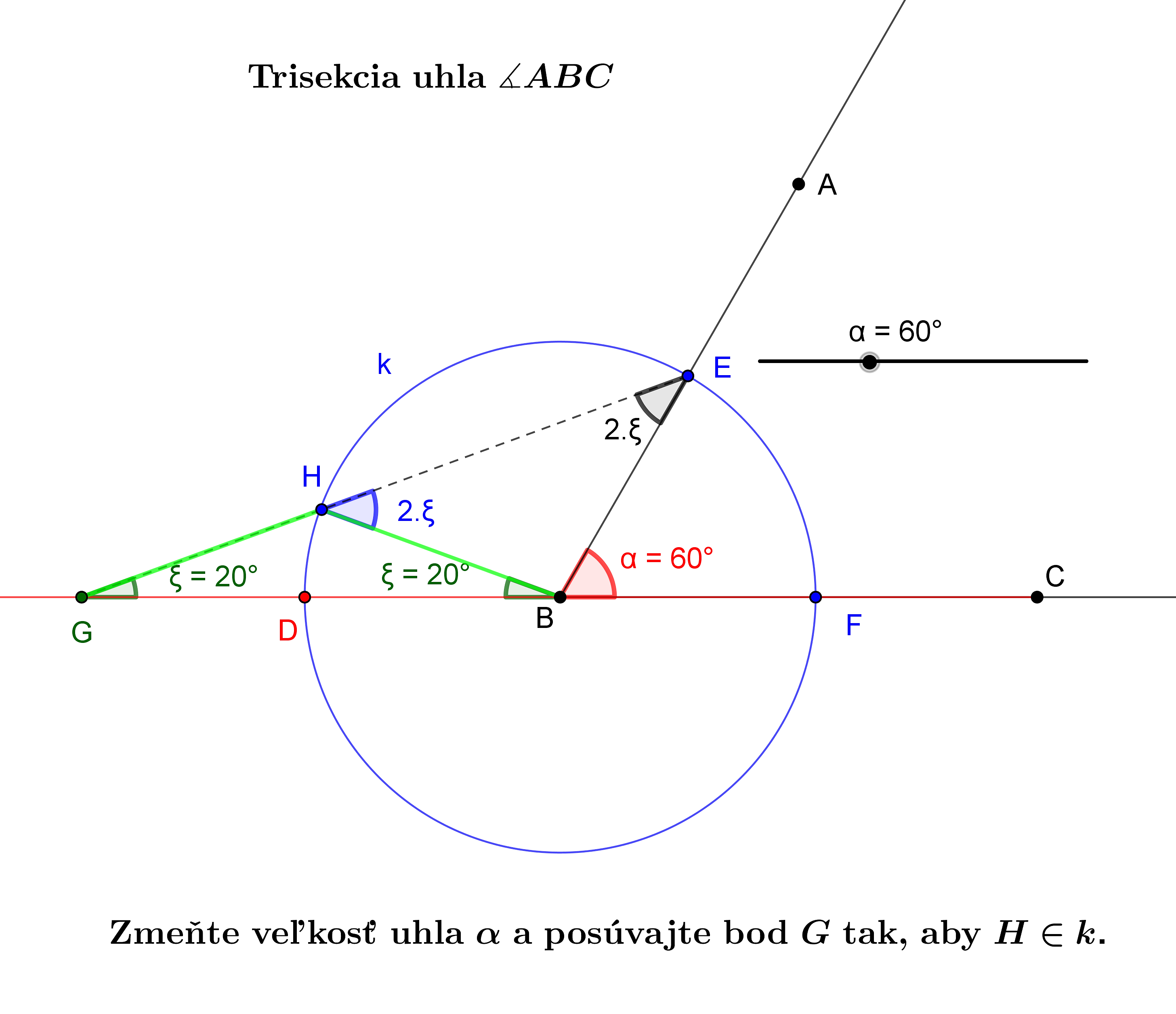
Nami predložená konštrukcia nie je riešenie známeho problému "trisekcia uhla". Pri riešení využívame postulát Post 2, ktorý zaručuje existenciu bodov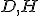 .
.
Konštrukcia umožňuje s dostatočnou presnosťou nájsť polohu bodu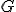 tak, aby sa veľkosť úsečky
tak, aby sa veľkosť úsečky 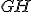 približovala (postupným posúvaním bodu
približovala (postupným posúvaním bodu 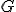 po priamke
po priamke  ) k veľkosti polomeru
) k veľkosti polomeru 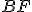 a tým aj uhol
a tým aj uhol 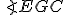 k
k 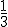 veľkosti uhla
veľkosti uhla 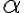 .
.
Ak si vopred stanovíme presnosť veľkosti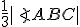 na
na  desatinných miest,
tak túto úlohu môžeme úspešne riešiť využitím skriptovania v programe GeoGebra.
desatinných miest,
tak túto úlohu môžeme úspešne riešiť využitím skriptovania v programe GeoGebra.
Nami predložená konštrukcia nie je riešenie známeho problému "trisekcia uhla". Pri riešení využívame postulát Post 2, ktorý zaručuje existenciu bodov
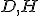 .
.
Konštrukcia umožňuje s dostatočnou presnosťou nájsť polohu bodu
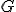 tak, aby sa veľkosť úsečky
tak, aby sa veľkosť úsečky 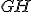 približovala (postupným posúvaním bodu
približovala (postupným posúvaním bodu 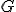 po priamke
po priamke  ) k veľkosti polomeru
) k veľkosti polomeru 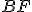 a tým aj uhol
a tým aj uhol 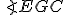 k
k 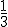 veľkosti uhla
veľkosti uhla 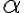 .
.
Ak si vopred stanovíme presnosť veľkosti
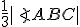 na
na  desatinných miest,
tak túto úlohu môžeme úspešne riešiť využitím skriptovania v programe GeoGebra.
desatinných miest,
tak túto úlohu môžeme úspešne riešiť využitím skriptovania v programe GeoGebra.