Interaktívna geometria - planimetria
Spojitosť
Tvrdenie T/1 (Euklidove Základy Kniha 1, Tvrdenie I).
K danej úsečke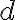 zostrojte rovnostranný trojuholník tak, aby táto úsečka bola jednou z jeho strán.
zostrojte rovnostranný trojuholník tak, aby táto úsečka bola jednou z jeho strán.
Dôkaz.
Dôkaz má konštrukčný charakter. Euklides popisuje konštrukciu rovnostranného trojuholníka pomocou kružníc
pomocou kružníc
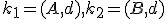 , ktoré sa pretínajú v dvoch rôznych bodoch.
, ktoré sa pretínajú v dvoch rôznych bodoch.
K danej úsečke
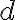 zostrojte rovnostranný trojuholník tak, aby táto úsečka bola jednou z jeho strán.
zostrojte rovnostranný trojuholník tak, aby táto úsečka bola jednou z jeho strán.
Dôkaz.
Dôkaz má konštrukčný charakter. Euklides popisuje konštrukciu rovnostranného trojuholníka
 pomocou kružníc
pomocou kružníc
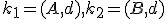 , ktoré sa pretínajú v dvoch rôznych bodoch.
, ktoré sa pretínajú v dvoch rôznych bodoch.
Poznámky.
- V Euklidových Základoch sa nenachádza axióma alebo tvrdenie, podľa ktorého je zaručená existencia spoločného bodu dvoch kružníc!
- V e-knihe DGS sme už uviedli, že v afinnom priestore nad poľom racionálnych čísel sa kruhy nepretínajú.
- Euklides síce nehovorí o spoločnom bode dvoch kružníc, uvádza len tvrdenie/formuláciu "... v ktorom sa kruhy navzájom pretínajú, ..."
- Vyriešiť tento problém je možné sformulovaním axióm spojitosti.
Axiómy spojitosti.
S1: (Archimedova axióma) Nech sú dané úsečky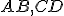 . Na polpriamke
. Na polpriamke
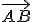 zostrojme postupne body
zostrojme postupne body
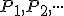 také, že
také, že
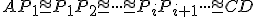 .
.
Potom existuje jediné prirodzené číslo také, že bod
také, že bod
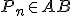 a
a
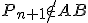 .
.
S2: (Axióma úplnosti) K bodom a priamkam v rovine už nie je možné pridať ďalšie tak, aby výsledná geometria stále spĺňala všetky doteraz uvedené axiómy
S1: (Archimedova axióma) Nech sú dané úsečky
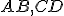 . Na polpriamke
. Na polpriamke
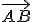 zostrojme postupne body
zostrojme postupne body
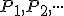 také, že
také, že
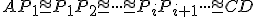 .
.
Potom existuje jediné prirodzené číslo
 také, že bod
také, že bod
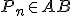 a
a
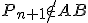 .
.
S2: (Axióma úplnosti) K bodom a priamkam v rovine už nie je možné pridať ďalšie tak, aby výsledná geometria stále spĺňala všetky doteraz uvedené axiómy
Poznámky.
- Euklidovská rovina je model všetkých uvedených axióm.
- Euklidovská rovina je afinná rovina
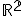 so skalárnym súčinom definovaným na jej vektorovej zložke. Používame aj označenie
so skalárnym súčinom definovaným na jej vektorovej zložke. Používame aj označenie 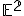 .
. - Geometria, ktorá spĺňa všetky Hilbertove axiómy (dôležitá je pritom Archimedova axióma), môžeme v nej zaviesť meranie! Pozrite si e-knihu "Miera úsečky".
