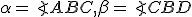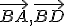Interaktívna geometria - planimetria
Zhodnosť
Geometria uhlov
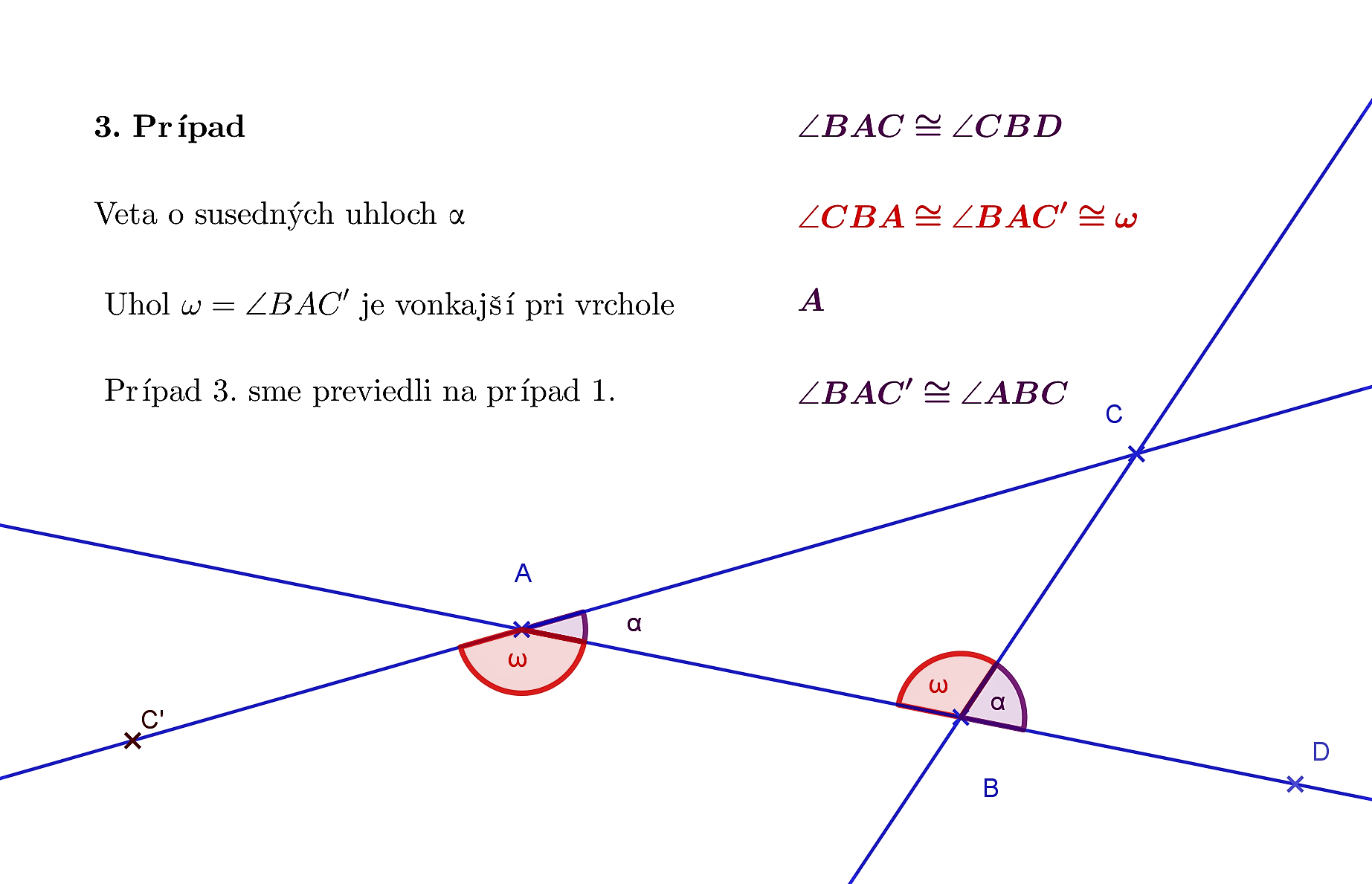
Tvrdenie.
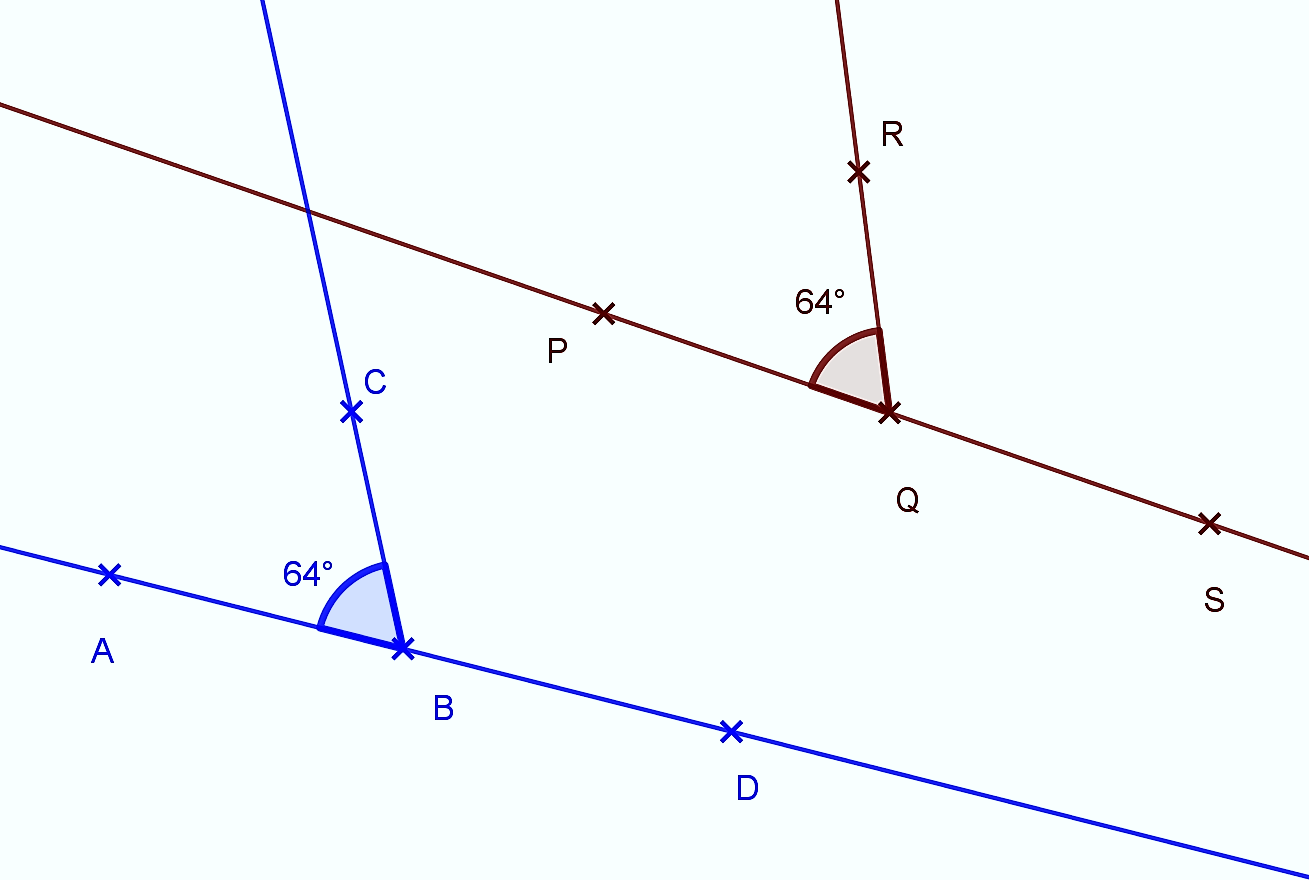
Ak sú dva uhly zhodné, potom aj ich susedné uhly sú zhodné.
Ak sú dva uhly zhodné, potom aj ich susedné uhly sú zhodné.
Dôkaz.
Definícia (Vonkajší uhol trojuholníka).
Vonkajší uhol trojuholníka je uhol susedný s priľahlým vnútorným uhlom trojuholníka.
Vonkajší uhol trojuholníka je uhol susedný s priľahlým vnútorným uhlom trojuholníka.
Napríklad v predchádzajúcej vete je uhol
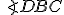 vonkajší uhol k uhlu
vonkajší uhol k uhlu
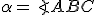 . Existenciu bodu
. Existenciu bodu
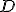 zabezpečuje axióma Z1 a axióma U2.
zabezpečuje axióma Z1 a axióma U2.
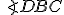 vonkajší uhol k uhlu
vonkajší uhol k uhlu
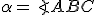 . Existenciu bodu
. Existenciu bodu
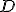 zabezpečuje axióma Z1 a axióma U2.
zabezpečuje axióma Z1 a axióma U2.
Tvrdenie.
Vonkajší uhol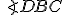 v trojuholníku
v trojuholníku
 susedný k uhlu
susedný k uhlu 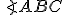 je väčší ako ľubovoľný zo zvyšných dvoch vnútorných uhlov tohto trojuholníka. Symbolicky zapísané
je väčší ako ľubovoľný zo zvyšných dvoch vnútorných uhlov tohto trojuholníka. Symbolicky zapísané
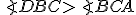 a zároveň
a zároveň
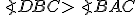 .
.
Vonkajší uhol
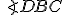 v trojuholníku
v trojuholníku
 susedný k uhlu
susedný k uhlu 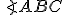 je väčší ako ľubovoľný zo zvyšných dvoch vnútorných uhlov tohto trojuholníka. Symbolicky zapísané
je väčší ako ľubovoľný zo zvyšných dvoch vnútorných uhlov tohto trojuholníka. Symbolicky zapísané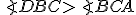 a zároveň
a zároveň
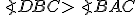 .
.
Dôkaz.
Stačí, keď dokážeme platnosť prvého a druhého prípadu. Budeme dokazovať sporom.
Stačí, keď dokážeme platnosť prvého a druhého prípadu. Budeme dokazovať sporom.
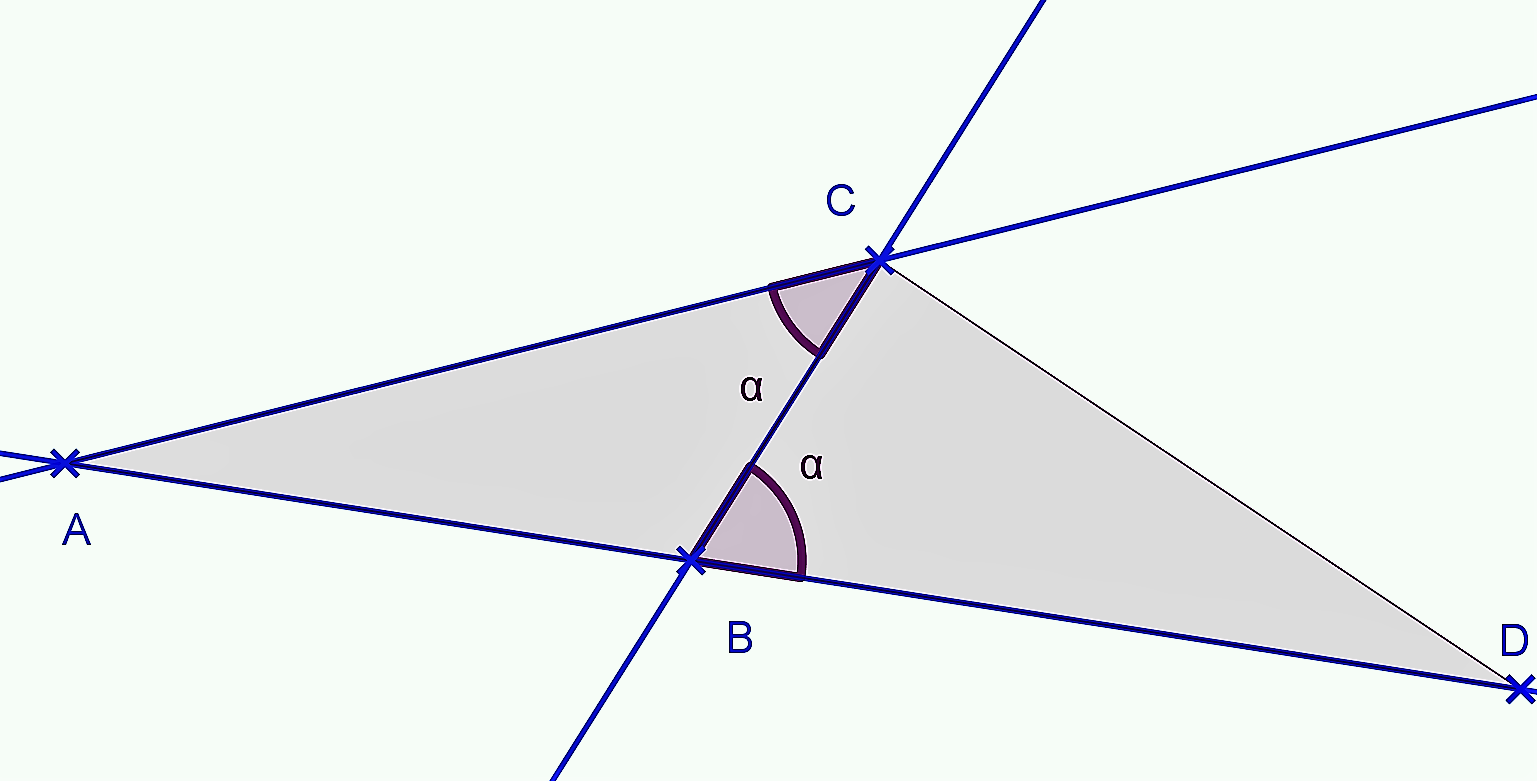
- Nech platí
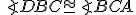 a zároveň nech
a zároveň nech
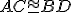 , potom
, potom
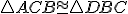 .
.
Odtiaľ dostávame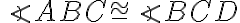 .
.
Zároveň zo zhodnosti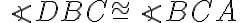 a z tvrdenia o susedných uhloch dostávame
a z tvrdenia o susedných uhloch dostávame
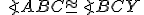 , kde
, kde
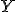 je bod na polpriamke
je bod na polpriamke
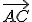 taký, že
taký, že
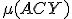 .
.
Polpriamky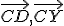 obe zvierajú s
obe zvierajú s
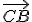 rovnaký uhol, pričom body
rovnaký uhol, pričom body
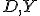 ležia na tej istej strane od
ležia na tej istej strane od
 (sú oba na opačnej ako
(sú oba na opačnej ako
 ). To je spor s axiómou Z4.
). To je spor s axiómou Z4.
- Nech platí
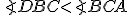 ,
,
potom existuje polpriamka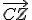 medzi polpriamkami
medzi polpriamkami
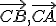 tak, že platí
tak, že platí
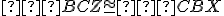 .
.
Teraz tento prípad prevedieme na prvý prípad, ktorého platnosť sme už dokázali. Polpriamka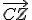 pretína pretína úsečku
pretína pretína úsečku
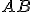 (veta o priečke uhla, Chalmovianska, str. 19) v bode
(veta o priečke uhla, Chalmovianska, str. 19) v bode 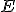 . Potom v trojuholníku
. Potom v trojuholníku
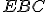 je vonkajší uhol pri vrchole
je vonkajší uhol pri vrchole
 zhodný s vnútorným uhlom pri vrchole
zhodný s vnútorným uhlom pri vrchole
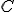 . To je ale predpoklad prvého prípadu. To však viedlo k sporu, preto nemôže nastať ani druhý prípad.
. To je ale predpoklad prvého prípadu. To však viedlo k sporu, preto nemôže nastať ani druhý prípad. - V ďalších dvoch prípadoch
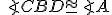 ;
;
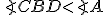 postupujeme analogicky.
postupujeme analogicky.
Poznámky.
- Euklides tvrdenie o vonkajšom uhle (uvádza vo svojich Základoch ako tvrdenie T/XVI, pozrite Tu) dokazuje pomocou zhodnosti vrcholových uhlov. V dôkaze využíva vlastnosť (ktorú bližšie nešpecifikuje), že pri "prenášaní" úsečky sa jej veľkosť nemení.
- V Euklidovom dôkaze kľúčovým momentom je predpoklad, že polpriamka
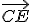 leží medzi polpriamkami
leží medzi polpriamkami
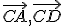 . To Euklides pokladá za všeobecne platnú Zásadu. U Hilberta je to podložené axiómami zhodnosti a usporiadania.
. To Euklides pokladá za všeobecne platnú Zásadu. U Hilberta je to podložené axiómami zhodnosti a usporiadania.
- Zhodnosť vrcholových uhlov dokazuje pomocou vlastnosti, že súčet susedných uhlov sa rovná dvom pravým uhlom. Tvrdenie T/XV, dôkaz pozrite Tu.
- V stredoškolskej matematike sa táto veta uvádza ako Teoréma vonkajšieho uhla. Pozri Wikipédiu Tu