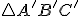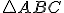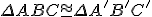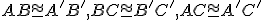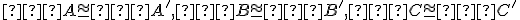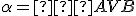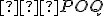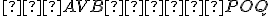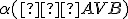Interaktívna geometria - planimetria
Zhodnosť
Axiómy zhodnosti
Z1: Pre ľubovoľné dva rôzne body a polpriamku vychádzajúcu z bodu
a polpriamku vychádzajúcu z bodu 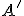
existuje na tejto polpriamke práve jeden bod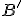 taký,
že
taký,
že 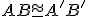 .
.
Z2: Ak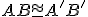 a
a 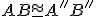 , potom
, potom 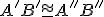 .
.
Navyše, každá úsečka je zhodná sama so sebou: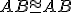 .
.
Z3: Ak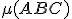 ,
,
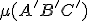 ,
,
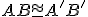 a
a
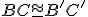 , potom
, potom
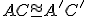 .
.
Z4: Pre daný uhol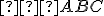 , danú polpriamku
, danú polpriamku
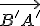 a danú polrovinu ohraničenú priamkou
a danú polrovinu ohraničenú priamkou
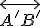
existuje práve jedna polpriamka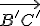 v danej polrovine tak, že
v danej polrovine tak, že
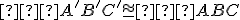 .
.
Z5: Ak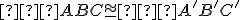 a
a
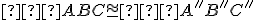 , potom
, potom
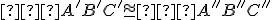 .
.
Navyše, každý uhol je zhodný sám so sebou: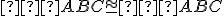 .
.
Z6: Ak pre trojuholníky a
a
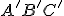 platí, že
platí, že
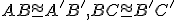 a
a
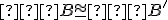 ,
,
potom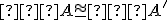 a
a
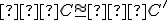 .
.
Z1: Pre ľubovoľné dva rôzne body
 a polpriamku vychádzajúcu z bodu
a polpriamku vychádzajúcu z bodu 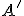
existuje na tejto polpriamke práve jeden bod
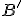 taký,
že
taký,
že 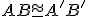 .
.
Z2: Ak
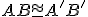 a
a 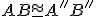 , potom
, potom 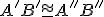 .
.
Navyše, každá úsečka je zhodná sama so sebou:
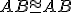 .
.
Z3: Ak
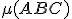 ,
,
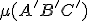 ,
,
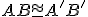 a
a
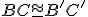 , potom
, potom
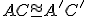 .
.
Z4: Pre daný uhol
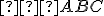 , danú polpriamku
, danú polpriamku
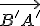 a danú polrovinu ohraničenú priamkou
a danú polrovinu ohraničenú priamkou
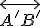
existuje práve jedna polpriamka
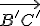 v danej polrovine tak, že
v danej polrovine tak, že
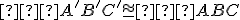 .
.
Z5: Ak
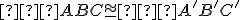 a
a
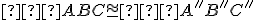 , potom
, potom
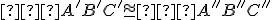 .
.
Navyše, každý uhol je zhodný sám so sebou:
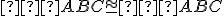 .
.
Z6: Ak pre trojuholníky
 a
a
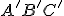 platí, že
platí, že
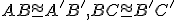 a
a
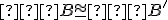 ,
,
potom
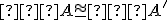 a
a
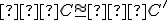 .
.
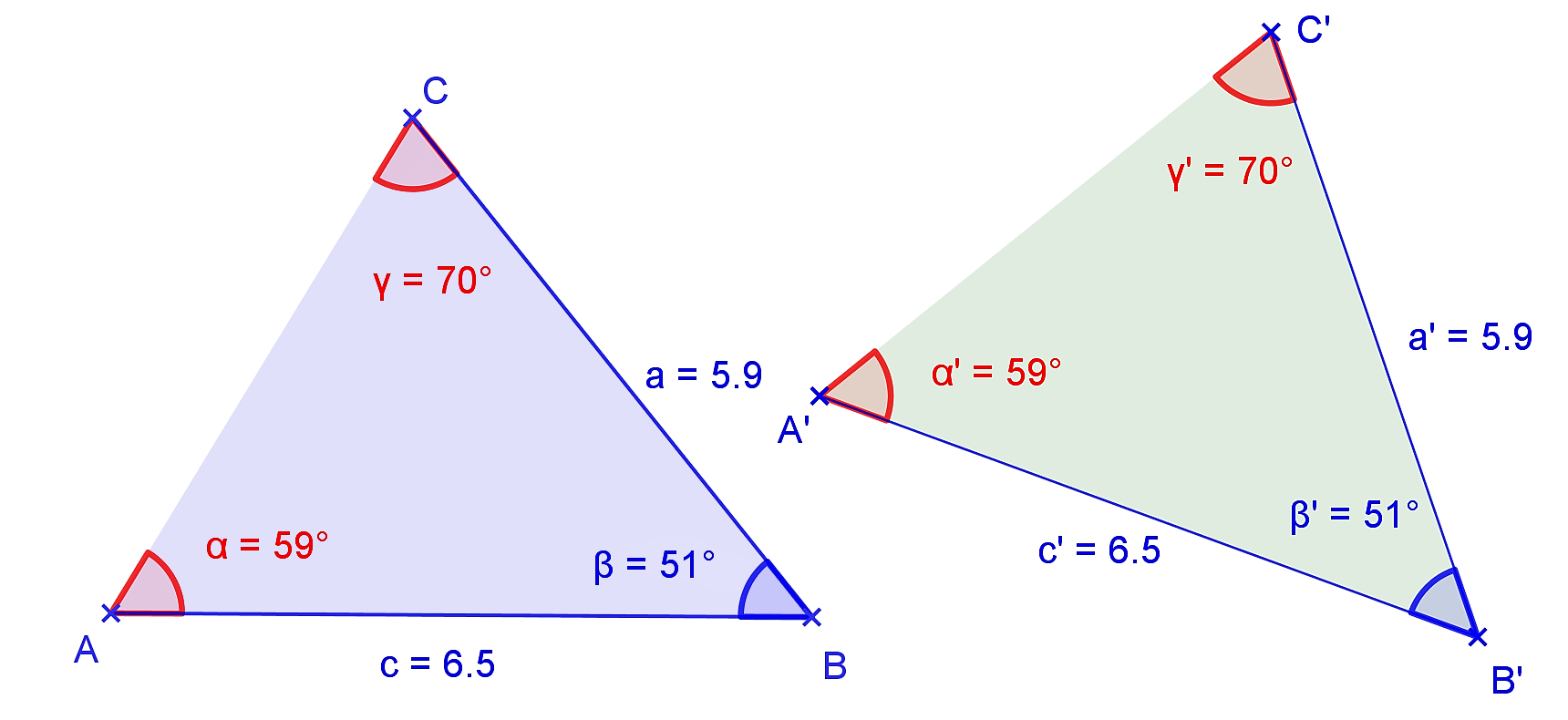
Veta sus. (Euklidove Základy, Tvrdenie I.4)
Ak pre trojuholníky a
a
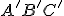 platí, že
platí, že
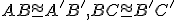 a
a
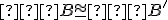 , potom sú tieto trojuholníky zhodné.
, potom sú tieto trojuholníky zhodné.
Ak pre trojuholníky
 a
a
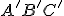 platí, že
platí, že
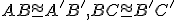 a
a
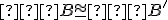 , potom sú tieto trojuholníky zhodné.
, potom sú tieto trojuholníky zhodné.
Dôkaz.
V dôsledku axiómy Z6 stačí ukázať, že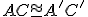 .
Dôkaz urobíme sporom. Nech
.
Dôkaz urobíme sporom. Nech
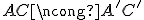 .
.
Nech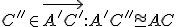 , pre ktorý platí
, pre ktorý platí
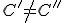 . Použitím axiómy Z6 dostaneme, že
. Použitím axiómy Z6 dostaneme, že
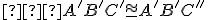 ,
,
čo je v rozpore s axiómou Z4 o prenášaní uhla. Teda musí platiť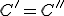 .
.
V dôsledku axiómy Z6 stačí ukázať, že
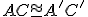 .
Dôkaz urobíme sporom. Nech
.
Dôkaz urobíme sporom. Nech
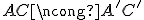 .
.
Nech
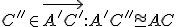 , pre ktorý platí
, pre ktorý platí
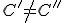 . Použitím axiómy Z6 dostaneme, že
. Použitím axiómy Z6 dostaneme, že
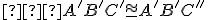 ,
,
čo je v rozpore s axiómou Z4 o prenášaní uhla. Teda musí platiť
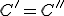 .
.
Poznámky.
- Niekedy sa veta sus uvádza ako axióma Z6.
- Porovnajte nami prezentovaný dôkaz vety sus s dôkazom v uvedeným v Euklidových Základoch.
- Ďalšie vety o zhodnosti trojuholníkov nájdete v samostatnej e-knihe tohto kurzu.
V Hilbertovom axiomatickom systéme axiómy Z1 a Z4 zaručujú jednoznačnosť prenášania
- danej úsečky na danú polpriamku - Z1
- uhla danej veľkosti do polroviny - Z4
Definícia.
Nech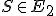 je ľubovoľný bod a
je ľubovoľný bod a  je daná nenulová úsečka. Kružnica so stredom
je daná nenulová úsečka. Kružnica so stredom
 a polomerom
a polomerom  je množina všetkých bodov
je množina všetkých bodov
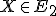 , pre ktoré platí, že úsečka
, pre ktoré platí, že úsečka
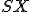 je zhodná s úsečkou
je zhodná s úsečkou  .
.
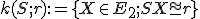
Nech
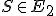 je ľubovoľný bod a
je ľubovoľný bod a  je daná nenulová úsečka. Kružnica so stredom
je daná nenulová úsečka. Kružnica so stredom
 a polomerom
a polomerom  je množina všetkých bodov
je množina všetkých bodov
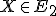 , pre ktoré platí, že úsečka
, pre ktoré platí, že úsečka
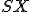 je zhodná s úsečkou
je zhodná s úsečkou  .
.
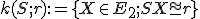
Definície ďalších geometrických útvarov budeme uvádzať priebežne podľa potreby.
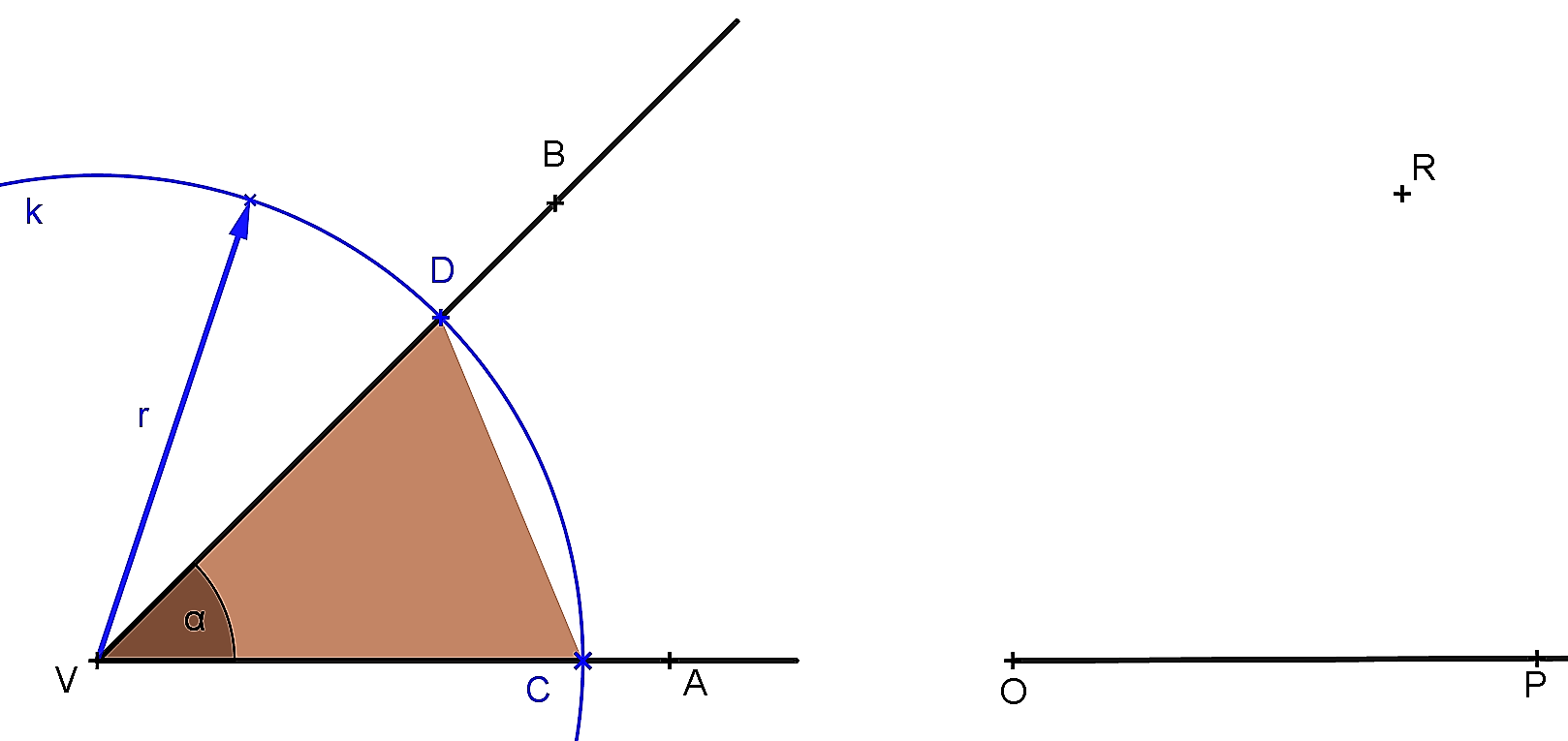
Axióma Z4 predstavuje euklidovskú konštrukciu prenášania uhla do danej polroviny. Vo vyučovaní geometrie na ZŠ sa táto konštrukcia uskutočňuje pomocou listu papiera alebo pomocou kružidla. Dynamickú formu aktivity prenášania uhla pomocou kružidla, ktorá je vhodná pre žiakov základných škôl, predstavuje nasledujúci applet.
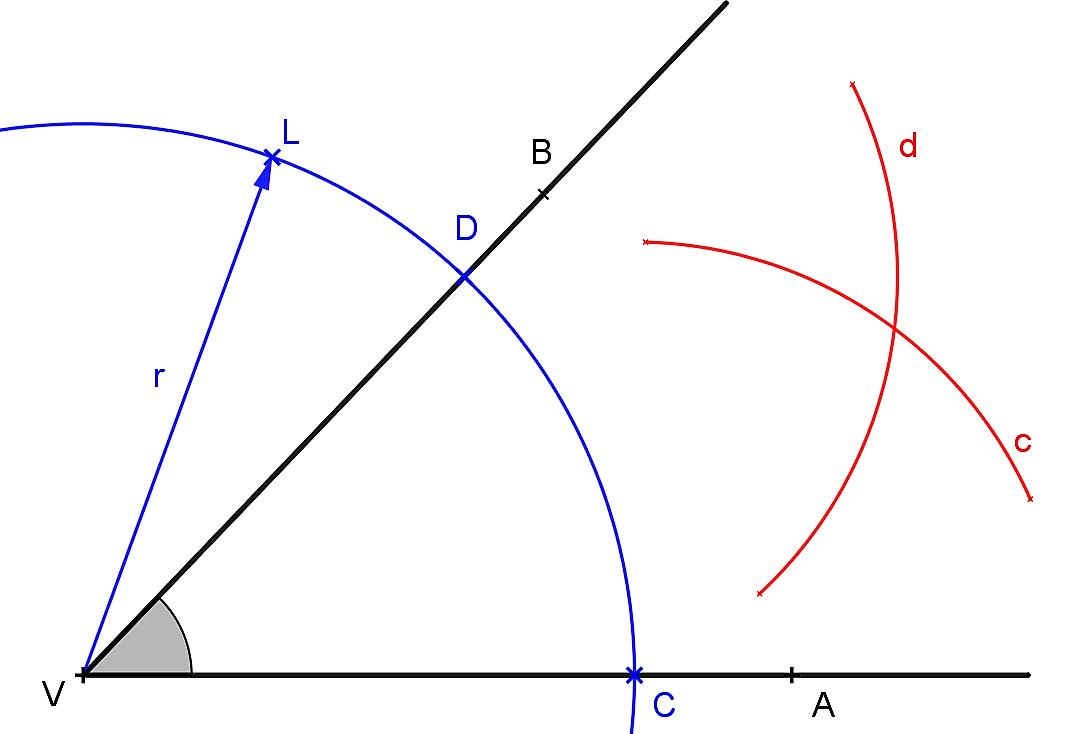
Kružnica sa využíva aj pri euklidovskej konštrukcii osi uhla Kniha 1, Tvrdenie IX ako ukazuje nasledujúci obrázok.
V predchádzajúcich dvoch euklidovských konštrukciách sa mimovoľne predpokladalo, že pri prenášaní úsečky jej veľkosť sa nemení. V Hilbertovom axiomatickom systéme vlastnosť zachovávania "veľkosti útvaru" pri "prenášaní" sa zaručuje pomocou axióm Z1 a Z4.
Rozdiel medzi Euklidovými Základmi a Hilbertovým axiomatickým prístupom je zásadný, ktorý podrobnejšie popíšeme v nasledujúcej podkapitole.
Axióma Z4 predstavuje euklidovskú konštrukciu prenášania uhla do danej polroviny. Vo vyučovaní geometrie na ZŠ sa táto konštrukcia uskutočňuje pomocou listu papiera alebo pomocou kružidla. Dynamickú formu aktivity prenášania uhla pomocou kružidla, ktorá je vhodná pre žiakov základných škôl, predstavuje nasledujúci applet.
Kružnica sa využíva aj pri euklidovskej konštrukcii osi uhla Kniha 1, Tvrdenie IX ako ukazuje nasledujúci obrázok.
V predchádzajúcich dvoch euklidovských konštrukciách sa mimovoľne predpokladalo, že pri prenášaní úsečky jej veľkosť sa nemení. V Hilbertovom axiomatickom systéme vlastnosť zachovávania "veľkosti útvaru" pri "prenášaní" sa zaručuje pomocou axióm Z1 a Z4.
Rozdiel medzi Euklidovými Základmi a Hilbertovým axiomatickým prístupom je zásadný, ktorý podrobnejšie popíšeme v nasledujúcej podkapitole.