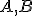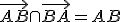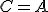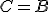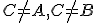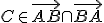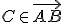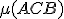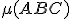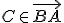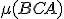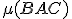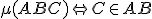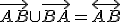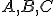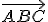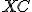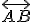Interaktívna geometria - planimetria
Usporiadanie
Axiómy usporiadania
U1: Ak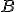 leží medzi
leží medzi
 a
a
 [
[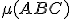 ], potom
], potom
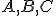 sú tri rôzne kolineárne body a platí tiež, že
sú tri rôzne kolineárne body a platí tiež, že
 leží medzi
leží medzi
 a
a
 .
.
U2: Pre ľubovoľné navzájom rôzne body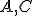 existujú body
existujú body
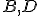 tak, že
tak, že
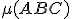 a
a
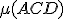 .
.
U3: Pre ľubovoľné tri navzájom rôzne kolineárne body práve jeden z nich leží medzi zvyšnými dvoma.
U4: (Paschova axióma, 1882) Nech priamka neprechádza žiadnym z nekolineárnych bodov
neprechádza žiadnym z nekolineárnych bodov
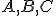 .
.
Ak pretína úsečku
pretína úsečku
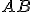 , potom pretína buď úsečku
, potom pretína buď úsečku
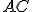 alebo úsečku
alebo úsečku
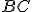 .
.
U1: Ak
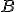 leží medzi
leží medzi
 a
a
 [
[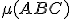 ], potom
], potom
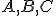 sú tri rôzne kolineárne body a platí tiež, že
sú tri rôzne kolineárne body a platí tiež, že
 leží medzi
leží medzi
 a
a
 .
.
U2: Pre ľubovoľné navzájom rôzne body
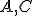 existujú body
existujú body
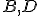 tak, že
tak, že
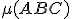 a
a
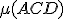 .
.
U3: Pre ľubovoľné tri navzájom rôzne kolineárne body práve jeden z nich leží medzi zvyšnými dvoma.
U4: (Paschova axióma, 1882) Nech priamka
 neprechádza žiadnym z nekolineárnych bodov
neprechádza žiadnym z nekolineárnych bodov
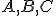 .
.
Ak
 pretína úsečku
pretína úsečku
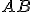 , potom pretína buď úsečku
, potom pretína buď úsečku
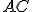 alebo úsečku
alebo úsečku
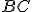 .
.
Definície.
- Nech
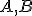 sú dva rôzne body. Úsečka
sú dva rôzne body. Úsečka
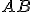 je množina bodov
je množina bodov
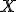 , ktoré ležia medzi bodmi
, ktoré ležia medzi bodmi
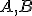 zjednotená s dvojprvkovou množinou
zjednotená s dvojprvkovou množinou
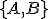 . Body
. Body
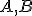 sú krajné body úsečky.
sú krajné body úsečky.
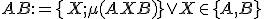
- Nech
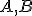 sú dva rôzne body. Polpriamka
sú dva rôzne body. Polpriamka
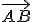 je množina bodov úsečky
je množina bodov úsečky
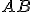 a bodov
a bodov
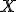 , pre ktoré platí
, pre ktoré platí
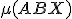 .
.
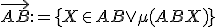
- Nech
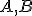 sú dva rôzne body. Opačná polpriamka k polpriamke
sú dva rôzne body. Opačná polpriamka k polpriamke
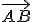 je množina bodov
je množina bodov
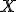 , pre ktoré platí, že bod
, pre ktoré platí, že bod
 leží medzi bodmi
leží medzi bodmi
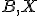 zjednotenú s jednobodovou množinou
zjednotenú s jednobodovou množinou
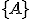 .
.
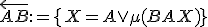
Dôkaz.
Z definície polpriamky dostávame
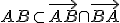 .
.
Potrebujeme ešte dokázať, že platí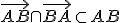 . Zvoľme si ľubovoľný bod
. Zvoľme si ľubovoľný bod 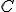 , pre ktorý platí
, pre ktorý platí
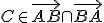 .
.
Z definície polpriamky dostávame
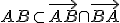 .
.
Potrebujeme ešte dokázať, že platí
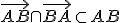 . Zvoľme si ľubovoľný bod
. Zvoľme si ľubovoľný bod 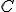 , pre ktorý platí
, pre ktorý platí
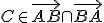 .
.
Dôkaz.
Dôkaz je nutné rozložiť do dvoch krokov (dokazujeme rovnosť množín).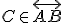 vzhľadom na
vzhľadom na
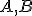 máme možnosti:
máme možnosti:
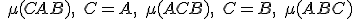 . Prvé tri možnosti znamenajú, že
. Prvé tri možnosti znamenajú, že
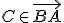
Dôkaz je nutné rozložiť do dvoch krokov (dokazujeme rovnosť množín).
- Nech
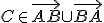 , potom treba dokázať
, potom treba dokázať 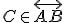 . Použite definíciu polriamky.
. Použite definíciu polriamky. - Nech
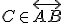 , potom treba dokázať
, potom treba dokázať 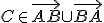 . Použite definíciu priamky.
. Použite definíciu priamky.
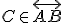 vzhľadom na
vzhľadom na
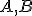 máme možnosti:
máme možnosti:
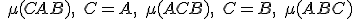 . Prvé tri možnosti znamenajú, že
. Prvé tri možnosti znamenajú, že
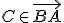
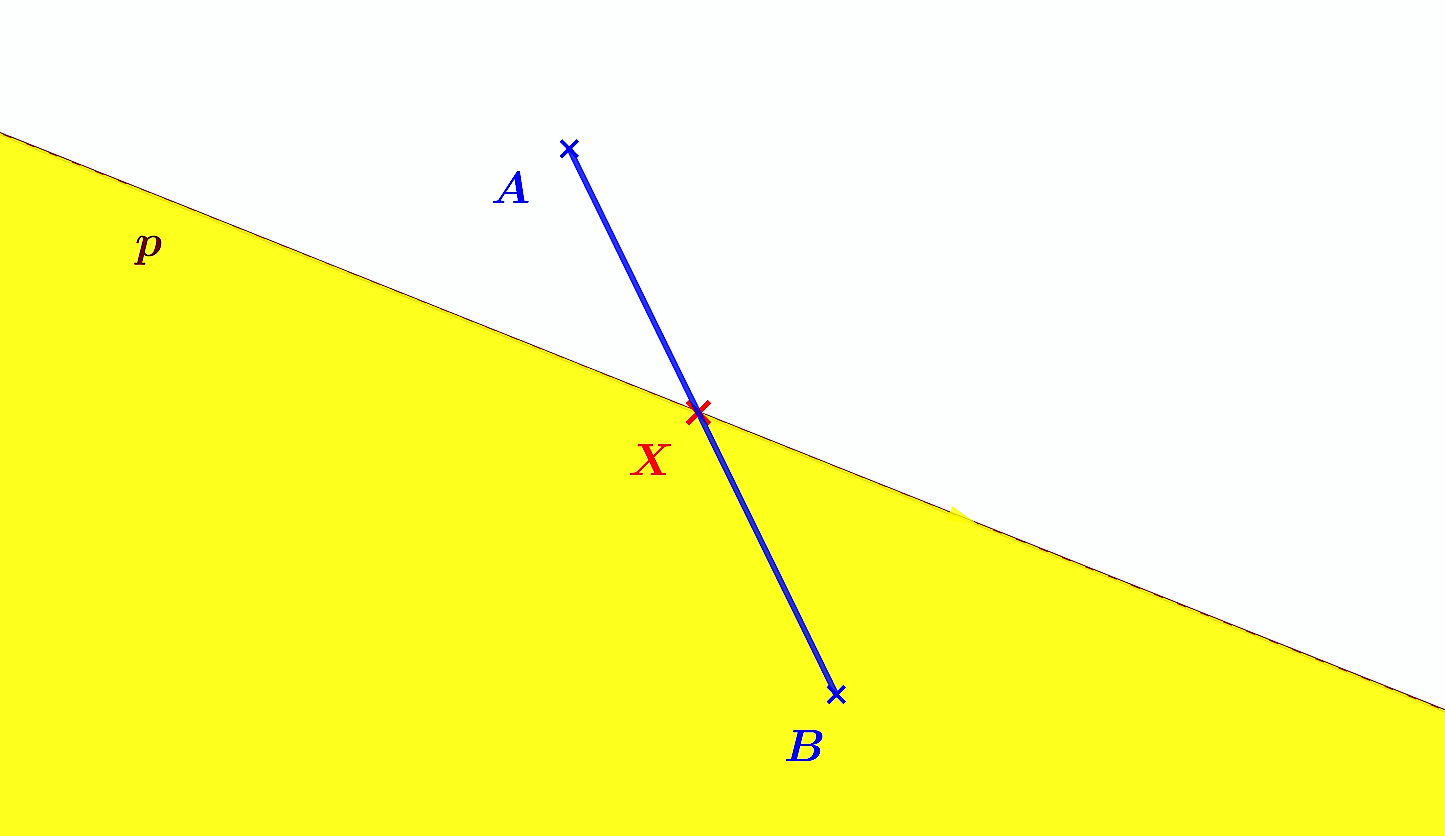
Definícia.
Daná je priamka a body
a body
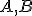 neležiace na tejto priamke. Hovoríme, že body
neležiace na tejto priamke. Hovoríme, že body
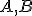
• ležia na opačných stranách od danej priamky, ak úsečka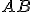 túto priamku pretína, t.j. ak na tejto priamke existuje bod
túto priamku pretína, t.j. ak na tejto priamke existuje bod
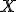 tak, že
tak, že 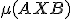
• ležia na tej istej strane od priamky , ak
, ak
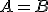 alebo ak
alebo ak
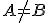 a úsečka
a úsečka
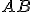 priamku
priamku  nepretína
(\\small ( p \cap AB= ∅ ) \)
nepretína
(\\small ( p \cap AB= ∅ ) \)
Daná je priamka
 a body
a body
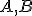 neležiace na tejto priamke. Hovoríme, že body
neležiace na tejto priamke. Hovoríme, že body
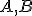
• ležia na opačných stranách od danej priamky, ak úsečka
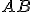 túto priamku pretína, t.j. ak na tejto priamke existuje bod
túto priamku pretína, t.j. ak na tejto priamke existuje bod
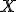 tak, že
tak, že 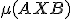
• ležia na tej istej strane od priamky
 , ak
, ak
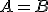 alebo ak
alebo ak
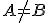 a úsečka
a úsečka
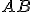 priamku
priamku  nepretína
(\\small ( p \cap AB= ∅ ) \)
nepretína
(\\small ( p \cap AB= ∅ ) \)
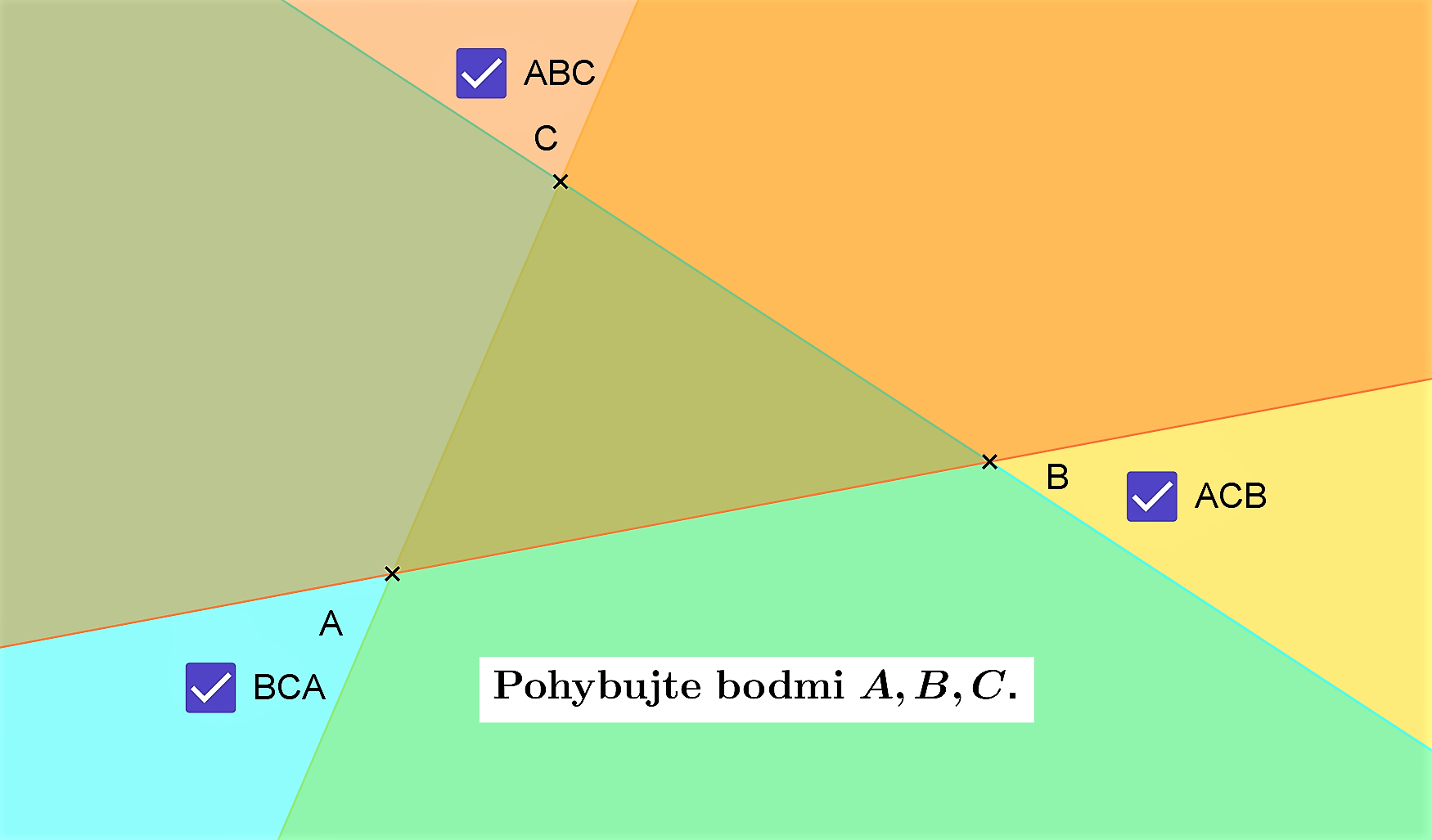
Príklad.
Dané sú tri nekolineárne body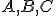 . Určte množinu (šrafovaním)
. Určte množinu (šrafovaním)
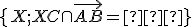 .
.
Konštrukčný návod Tu. Applet, v ktorom je nástroj na vyznačenie polroviny Tu.
Riešenie Tu.
Dané sú tri nekolineárne body
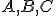 . Určte množinu (šrafovaním)
. Určte množinu (šrafovaním)
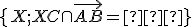 .
.
Konštrukčný návod Tu. Applet, v ktorom je nástroj na vyznačenie polroviny Tu.
Riešenie Tu.
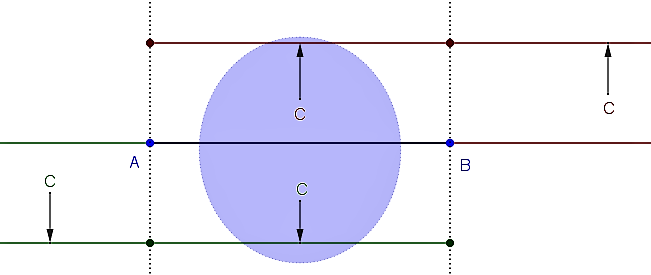
Tvrdenie (separačná vlastnosť v rovine, U4S).
Priamka delí rovinu okrem bodov priamky
delí rovinu okrem bodov priamky  na dve triedy tak, že body ležia v tej istej triede práve vtedy, keď
na dve triedy tak, že body ležia v tej istej triede práve vtedy, keď
ležia na tej istej strane od priamky . (t.j. neexistuje bod
. (t.j. neexistuje bod
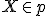 taký, že
taký, že
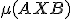 , kde
, kde  a
a
 sú dané body).
sú dané body).
Dôkaz pozri prácu [CHAL] .
Priamka
 delí rovinu okrem bodov priamky
delí rovinu okrem bodov priamky  na dve triedy tak, že body ležia v tej istej triede práve vtedy, keď
na dve triedy tak, že body ležia v tej istej triede práve vtedy, keď
ležia na tej istej strane od priamky
 . (t.j. neexistuje bod
. (t.j. neexistuje bod
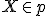 taký, že
taký, že
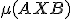 , kde
, kde  a
a
 sú dané body).
sú dané body).
Dôkaz pozri prácu [CHAL] .
Definície.
Pozrite si tiež definície v práci [MON] kapitola 2: "Konvexná množina".