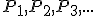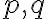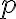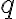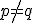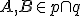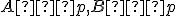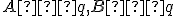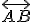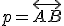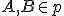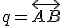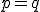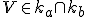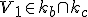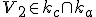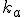Interaktívna geometria - planimetria
Hilbertov axiomatický systém
V roku 1899 slávny matematik David Hilbert publikoval prácu Grundlagen der Geometrie, v ktorej navrhuje axiomatický systém, nahrádzajúci tradičné axiómy Euklida. V literatúre je tento axiomatický systém známy ako Hilbertov axiomatický systém. V práci [HIL] je uvedených šesť primitívnych pojmov, ktoré sú začlenené do dvoch skupín:
- Primitívne objekty
- body - označujeme veľkými písmenami latinskej abecedy
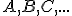 ;
; - priamky - na označenie používame malé písmená
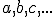 a
a - roviny - označujeme malými gréckymi písmenami
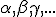 .
. - Primitívne vzťahy (binárne relácie)
- incidencia -
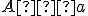 ["bod
["bod  leží na priamke
leží na priamke  ",
"priamka
",
"priamka  prechádza bodom
prechádza bodom  ", "bod
", "bod  a priamka
a priamka  sú incidentné"].
sú incidentné"]. - vzťah "medzi" - \small
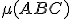 [usporiadanie troch kolineárnych bodov
[usporiadanie troch kolineárnych bodov
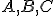 , kde bod
, kde bod  leží medzi bodmi
leží medzi bodmi 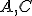 ]; používa sa aj označenie
]; používa sa aj označenie
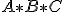 . Pozri prácu [ChalJ]
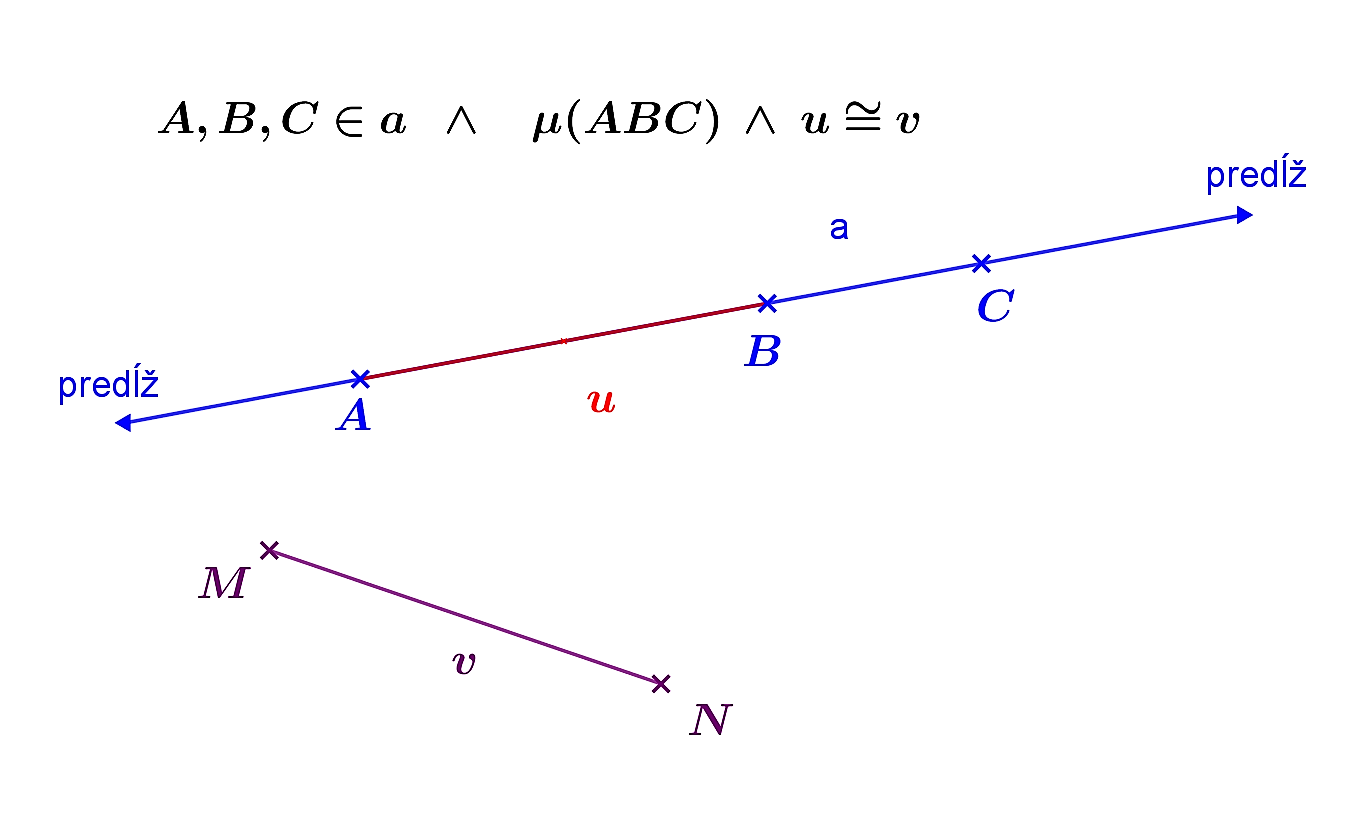
. Pozri prácu [ChalJ] - zhodnosť (kongruencia) -
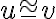 ["úsečka
["úsečka  je zhodná s úsečkou
je zhodná s úsečkou 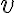 "], zhodnosť uhlov, zhodnosť trojuholníkov.
"], zhodnosť uhlov, zhodnosť trojuholníkov.
Hilbertov axiomatický systém pozostáva z piatich skupín axióm.
- axiómy incidencie
- axiómy usporiadania
- axiómy zhodnosti (kongruencie)
- axióma o rovnobežnosti
- axiómy spojitosti Axiómy charakterizujú vzťahy medzi primitívnymi objektmi. Axiomatický systém obsahuje celkom 20 axióm.
Axiómy incidencie v rovine
I1: Dvoma rôznymi bodmi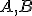 prechádza práve jedna priamka.
prechádza práve jedna priamka.
I2: Každá priamka obsahuje aspoň dva rôzne body.
I3: Existuje aspoň jedna trojica navzájom rôznych nekolineárnych bodov.
Axiómy incidencie v priestore
I4: Tromi nekolineárnymi bodmi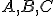 prechádza práve jedna rovina.
prechádza práve jedna rovina.
I5: V každej rovine existujú aspoň tri nekolineárne body.
I6: Ak dva rôzne body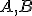 priamky
priamky 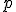 ležia v rovine
ležia v rovine 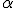 ,
potom každý bod priamky
,
potom každý bod priamky 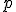 leží v rovine
leží v rovine 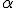 .
.
I7: Ak dve roviny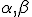 majú spoločný bod
majú spoločný bod
 , potom majú spoločný ešte aspoň jeden bod
, potom majú spoločný ešte aspoň jeden bod  , rôzny od
, rôzny od  .
.
I8: Existuje aspoň jedna štvorica nekomplanárnych bodov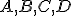 .
.
I1: Dvoma rôznymi bodmi
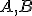 prechádza práve jedna priamka.
prechádza práve jedna priamka.
I2: Každá priamka obsahuje aspoň dva rôzne body.
I3: Existuje aspoň jedna trojica navzájom rôznych nekolineárnych bodov.
Axiómy incidencie v priestore
I4: Tromi nekolineárnymi bodmi
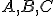 prechádza práve jedna rovina.
prechádza práve jedna rovina.
I5: V každej rovine existujú aspoň tri nekolineárne body.
I6: Ak dva rôzne body
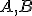 priamky
priamky 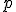 ležia v rovine
ležia v rovine 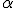 ,
potom každý bod priamky
,
potom každý bod priamky 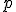 leží v rovine
leží v rovine 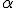 .
.
I7: Ak dve roviny
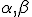 majú spoločný bod
majú spoločný bod
 , potom majú spoločný ešte aspoň jeden bod
, potom majú spoločný ešte aspoň jeden bod  , rôzny od
, rôzny od  .
.
I8: Existuje aspoň jedna štvorica nekomplanárnych bodov
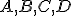 .
.
Dôkaz. nepriamo
V ďalšej časti sa zameriame na interpretáciu Euklidovskej roviny pomocou dynamických geometrických systémov (DGS). Budeme používať softvér GeoGebra. Vo všeobecnosti ak DGS má správne interpretovať danú geometriu (napr. Euklidovskú), tak je nutné vhodne popísať/definovať základné geometrické pojmy a vzťahy. Túto požiadavku výstižne charakterizuje doc. Vallo vo svojej habilitačnej práci, kde zdôrazňuje požiadavku determinovanosti pri využívaní IKT v geometrii.
V DGS je nutné, aby dôležité prvky geometrických útvarov boli deterministicky definované (Vallo, 2021).
Uvádzame niekoľko východísk, ktoré tvorcovia softvéru GeoGebra naprogramovali v jeho základnej verzii. Vo vzhľade Nákresňa (2-rozmerný priestor) je bod reprezentovaný dvojicou reálnych čísel. Tento model je izomorfný s afinným dvojrozmerným priestorom nad poľom reálnych čísel.
Požiadavka determinovanosti z pohľadu geometrie znamená presne stanoviť, čo predstavuje bod so súradnicami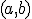 . Presné geometrické vymedzenie (determinovanosť) veľmi dobre interpretujú nasledovné príkazy softvéru GeoGebra.
. Presné geometrické vymedzenie (determinovanosť) veľmi dobre interpretujú nasledovné príkazy softvéru GeoGebra.
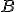 .
.
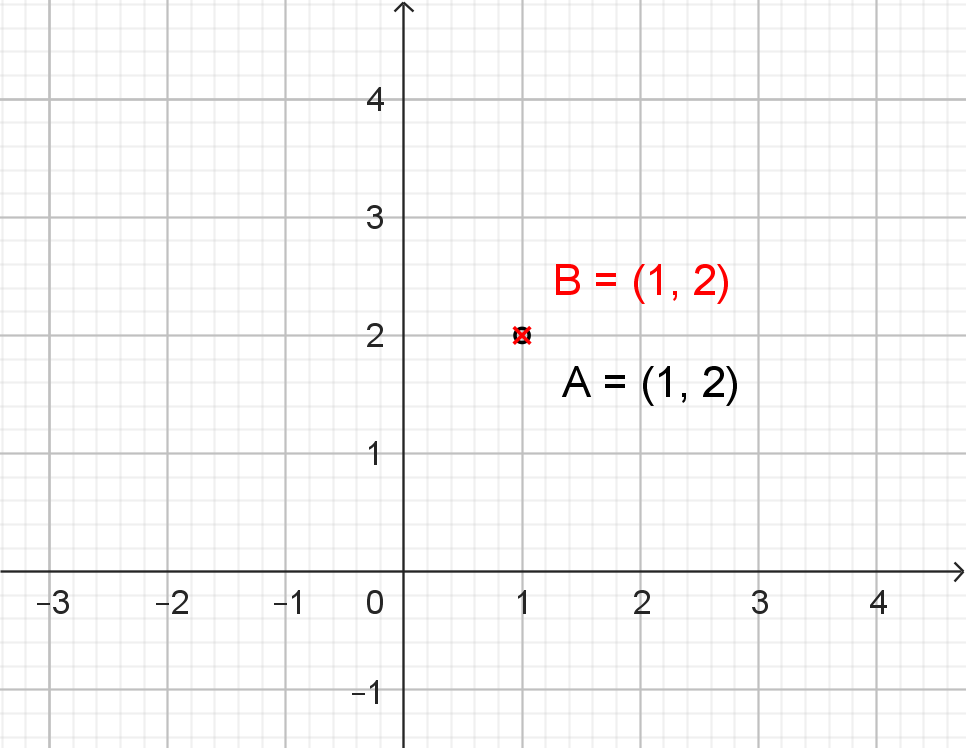
Pri klasickej výučbe geometrie (manuálne rysovacie prostriedky) je problematické reálne „pracovať“ s totožnými (identickými) útvarmi. Napríklad dva rôzne ale totožné body rozlíšime len tak, že pri ich popise uvedieme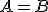 .
.
Požiadavka determinovanosti z pohľadu geometrie znamená presne stanoviť, čo predstavuje bod so súradnicami
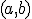 . Presné geometrické vymedzenie (determinovanosť) veľmi dobre interpretujú nasledovné príkazy softvéru GeoGebra.
. Presné geometrické vymedzenie (determinovanosť) veľmi dobre interpretujú nasledovné príkazy softvéru GeoGebra.
- Príkaz
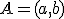 vygeneruje na zobrazovacej ploche bod so súradnicami
vygeneruje na zobrazovacej ploche bod so súradnicami
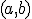 a s popisom
a s popisom
 .
.
- Príkaz
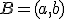 vygeneruje opäť bod s tými istými súradnicami a s popisom
vygeneruje opäť bod s tými istými súradnicami a s popisom
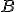 .
.
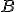 .
.
Pri klasickej výučbe geometrie (manuálne rysovacie prostriedky) je problematické reálne „pracovať“ s totožnými (identickými) útvarmi. Napríklad dva rôzne ale totožné body rozlíšime len tak, že pri ich popise uvedieme
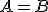 .
.
Poznámka.
V DGS priesečník dvoch priamok sa musí exaktne definovať pomocou nástroja Priesečník. Ak nie, tak DGS ho neidentifikuje ako bod.
V DGS priesečník dvoch priamok sa musí exaktne definovať pomocou nástroja Priesečník. Ak nie, tak DGS ho neidentifikuje ako bod.
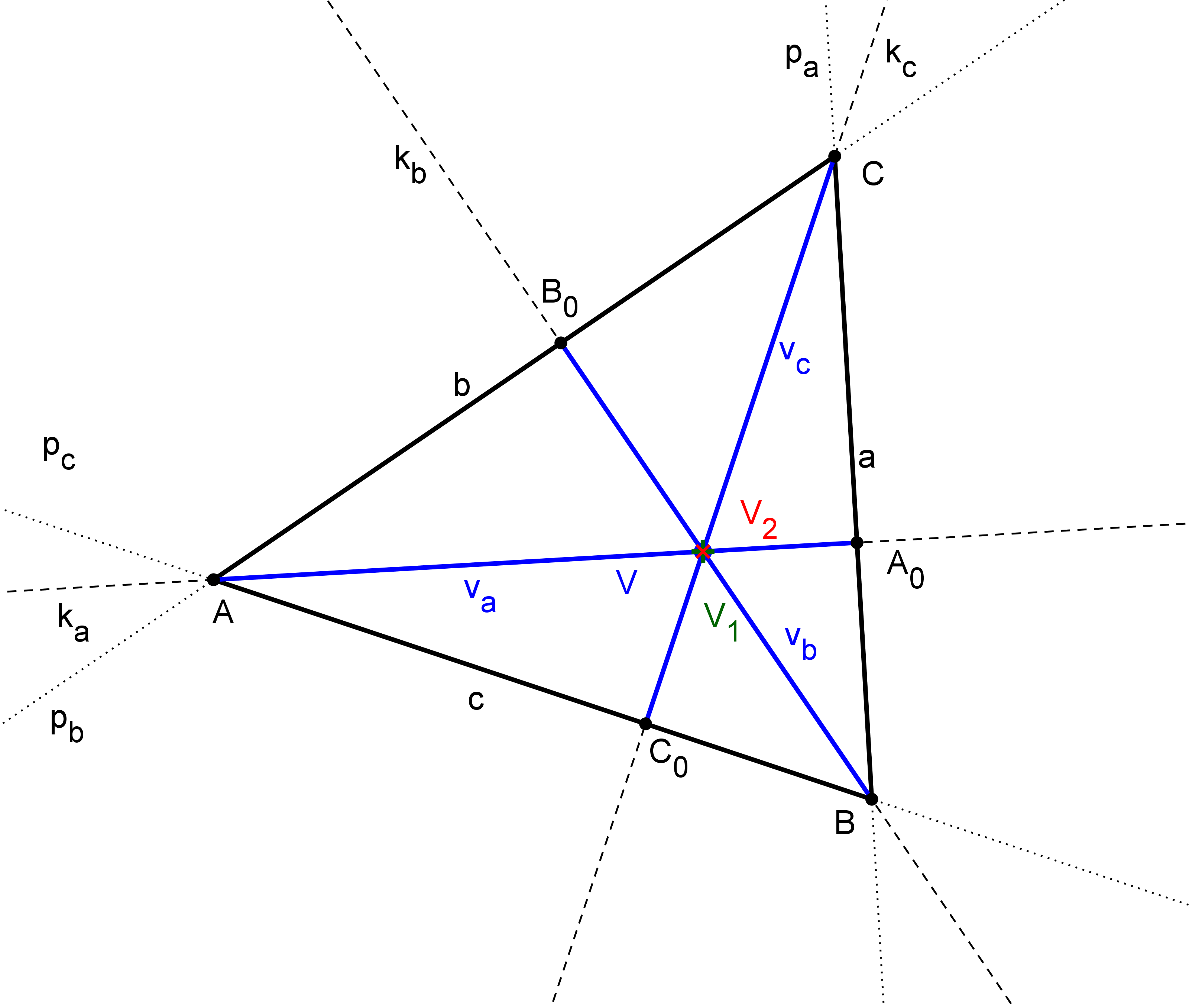
Pomocou nástroja " Priesečník" môžeme vytvoriť tri priesečníky výšok v trojuholníku
o ktorých vieme dokázať (Kapitola "Významné prvky trojuholníka"), že sú to tri totožné body.