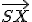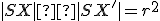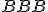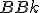Geometrické zobrazenia
Kruhová inverzia
Möbiova rovina je euklidovská rovina doplnená o jeden nevlastný bod 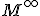 , ktorý budeme nazývať Möbiov bod.
, ktorý budeme nazývať Möbiov bod.
V takto doplnenej rovine môžeme definovať zobrazenie, ktoré sa nazýva kruhová inverzia.
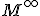 , ktorý budeme nazývať Möbiov bod.
, ktorý budeme nazývať Möbiov bod.
V takto doplnenej rovine môžeme definovať zobrazenie, ktoré sa nazýva kruhová inverzia.
Definícia 20
V Möbiovej rovine je daná kružnica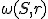 . Kruhová inverzia vzhľadom ku kružnici
. Kruhová inverzia vzhľadom ku kružnici 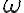 je zobrazenie, ktorého obrazom
je zobrazenie, ktorého obrazom
V Möbiovej rovine je daná kružnica
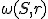 . Kruhová inverzia vzhľadom ku kružnici
. Kruhová inverzia vzhľadom ku kružnici 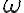 je zobrazenie, ktorého obrazom
je zobrazenie, ktorého obrazom
Poznamenajme, že
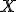 , ležiaci mimo kružnice
, ležiaci mimo kružnice 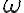 :
:
Z bodu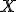 zostrojíme dotyčnicu kružnice
zostrojíme dotyčnicu kružnice 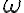 , bod dotyku označme
, bod dotyku označme 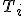 . Z bodu
. Z bodu 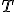 zostrojíme kolmicu na priamku
zostrojíme kolmicu na priamku 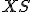 , päta tejto kolmice je hľadaný obraz
, päta tejto kolmice je hľadaný obraz 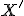 . Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice
. Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice 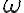 .
.
Kruhová inverzia je nelineárne zobrazenie, priamka až na špeciálne prípady sa nezobrazuje na priamku (priamky, ktoré neprechádzajú stredom inverzie, sa zobrazujú na kružnice).
- ak bod
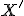 je obrazom bodu
je obrazom bodu 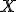 , potom je aj bod
, potom je aj bod 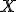 obrazom bodu
obrazom bodu 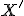 ,
dvojicu odpovedajúcich bodov nazývame aj navzájom inverzné body - kruhová inverzia je involútorné zobrazenie;
,
dvojicu odpovedajúcich bodov nazývame aj navzájom inverzné body - kruhová inverzia je involútorné zobrazenie; - body na kružnici
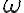 sú samodružné;
sú samodružné; - bod ležiaci vo vnútri kružnice
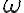 sa zobrazí na vonkajší bod a naopak.
Konštrukcia obrazu
sa zobrazí na vonkajší bod a naopak.
Konštrukcia obrazu
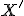 ľubovoľného bodu
ľubovoľného bodu 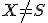 a
a 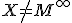 a
a 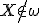 je založená na Euklidovej vete o odvesne.
je založená na Euklidovej vete o odvesne.
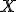 , ležiaci mimo kružnice
, ležiaci mimo kružnice 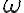 :
:
Z bodu
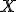 zostrojíme dotyčnicu kružnice
zostrojíme dotyčnicu kružnice 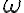 , bod dotyku označme
, bod dotyku označme 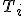 . Z bodu
. Z bodu 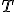 zostrojíme kolmicu na priamku
zostrojíme kolmicu na priamku 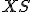 , päta tejto kolmice je hľadaný obraz
, päta tejto kolmice je hľadaný obraz 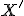 . Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice
. Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice 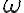 .
.
Kruhová inverzia je nelineárne zobrazenie, priamka až na špeciálne prípady sa nezobrazuje na priamku (priamky, ktoré neprechádzajú stredom inverzie, sa zobrazujú na kružnice).
Veta (Konformné zobrazenie).
Kruhová inverzia je konformné zobrazenie, t.j zachováva veľkosť uhla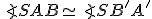 . Pozrite si obrázok "Konformné zobrazenie".
. Pozrite si obrázok "Konformné zobrazenie".
Kruhová inverzia je konformné zobrazenie, t.j zachováva veľkosť uhla
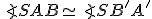 . Pozrite si obrázok "Konformné zobrazenie".
. Pozrite si obrázok "Konformné zobrazenie".
Dôkaz
Z definície kruhovej inverzie vyplýva
Obr. Konformné zobrazenie
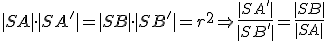
Teda trojuholníky
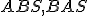 majú spoločný uhol pri vrchole, sú podľa vety
majú spoločný uhol pri vrchole, sú podľa vety 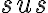 podobné.
podobné.
Tvrdenie (Obraz priamky a kružnice).
Body priamky prechádzajúcej stredom inverzie sa zobrazujú opäť na túto priamku.
sa zobrazujú opäť na túto priamku.
Body priamky prechádzajúcej stredom inverzie
 sa zobrazujú opäť na túto priamku.
sa zobrazujú opäť na túto priamku.
Dôkaz.
Ide vlastne o špeciálny prípad vety o konformnom zobrazení, keď bod
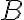 leží na kolmici k polpriamke
leží na kolmici k polpriamke 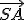 .
Zrejme platí
.
Zrejme platí
margin-left: 80px;">
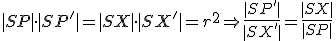 ,
,
lebo trojuholníky
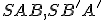 sú podobné. Uhol pri vrchole
sú podobné. Uhol pri vrchole 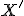 je pravý,
preto bod
je pravý,
preto bod 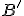 je zrejme bodom Thálesovej kružnice.
je zrejme bodom Thálesovej kružnice.
Dôsledky .
- Obrazom priamky
 , ktorá neprechádza stredom inverzie je kružnica
, ktorá neprechádza stredom inverzie je kružnica  prechádzajúca stredom
prechádzajúca stredom  .
. - Obrazom kružnice prechádzajúcej stredom inverzie je priamka, ktorá neprechádza stredom inverzie.
- Samodružnými bodmi sú body určujúcej kružnice
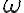 .
. - Samodružnými priamkami sú priamky prechádzajúce stredom inverzie.
- Samodružné kružnice sú tie, ktoré ortogonálne pretínajú určujúcu kružnicu. Dôkaz si môžete pozrieť v práci [JAN].
Dôkazy týchto dôsledkov sa opierajú o involútornosť kruhovej inverzie.
Tvrdenie (Obraz kružnice neprechádzajúcej stredom  ).
).
Obrazom kružnice, ktorá neprechádza stredom inverzie je kružnica.
je kružnica.
 ).
).
Obrazom kružnice, ktorá neprechádza stredom inverzie
 je kružnica.
je kružnica.
Poznámka.
Z obrázku "Obraz kružnice" je zrejmá jedna typická ale často opomínaná vlastnosť kruhovej inverzie:
Obrazom stredu kružnice nie je stred kružnice
nie je stred kružnice 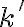 .
.
Z obrázku "Obraz kružnice" je zrejmá jedna typická ale často opomínaná vlastnosť kruhovej inverzie:
Obrazom stredu kružnice
 nie je stred kružnice
nie je stred kružnice 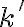 .
.
Apolloniova úloha.
Zostrojte kružnicu dotýkajúcu sa troch geometrických útvarov: bodu - , priamky -
, priamky -  , kružnice -
, kružnice -  .
.
Zostrojte kružnicu dotýkajúcu sa troch geometrických útvarov: bodu -
 , priamky -
, priamky -  , kružnice -
, kružnice -  .
.
- Existuje celkove desať možných kombinácií. Napr.
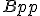 znamená zostrojiť kružnicu, ktorá prechádza bodom a dotýka sa dvoch priamok.
Dotyk s bodom znamená incidenciu s ním.
znamená zostrojiť kružnicu, ktorá prechádza bodom a dotýka sa dvoch priamok.
Dotyk s bodom znamená incidenciu s ním. - Najjednoduchšie prípady nastanú, keď sú dané tri body alebo tri priamky; tieto prípady vyriešil Euklides vo svojich Základoch. Apolloniove úlohy patria dodnes k najpríťažlivejším úlohám syntetickej geometrie.
Historické poznámky.
- O dotyku kružníc údajne písal už Archimedes. Jeho spis sa však nezachoval. Taktiež sa nezachoval dvojzväzkový pôvodný spis Apollonia z Pergy (262?-190? pred n. l.) „O dotykoch".
- Zmienil sa o ňom Pappos okolo roku 320, podľa ktorého Apollonios vyriešil všetky úlohy s výnimkou prípadu troch kružníc.
- Úlohu s tromi kružnicami riešil ako prvý F. Viete (1540-1603) v spise „Apollonius Gallus" (Paríž, r. 1600). V riešení použil stredy rovnoľahlosti troch kružníc.
- Vo všeobecnom prípade je osem výsledkov. Ak sa dané tri kružnice navzájom dotýkajú, riešenia sú dve (tzv. Soddyho kružnice).
Metódy riešenia Apolloniovej úlohy