Geometrické zobrazenia
Afinita
Geometrické zobrazenia 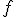 v euklidovskej rovine
v euklidovskej rovine 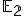 môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
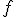 v euklidovskej rovine
v euklidovskej rovine 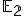 môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
Definícia (Samodružné prvky).
- Samodružný bod
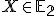 je bod, ktorý sa pri zobrazení
je bod, ktorý sa pri zobrazení  zobrazí sám na seba. Platí:
zobrazí sám na seba. Platí: 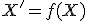 .
. - Samodružná priamka
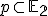 je priamka, ktorá sa pri zobrazení
je priamka, ktorá sa pri zobrazení  zobrazí sama na seba
zobrazí sama na seba 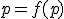 . Zároveň existuje bod
. Zároveň existuje bod 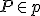 , ktorý sa zobrazí do bodu
, ktorý sa zobrazí do bodu 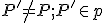 .
. - Priamka samodružných bodov je priamka, kde každý jej bod je samodružný. Pre každý bod na priamke platí X = X'. Hovoríme o bodovo samodružnej priamke.
Zvoľme si v euklidovskej rovine 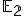 dve rôznobežné priamky
dve rôznobežné priamky 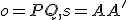 . Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie
. Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie 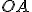 s vlastnosťami
s vlastnosťami
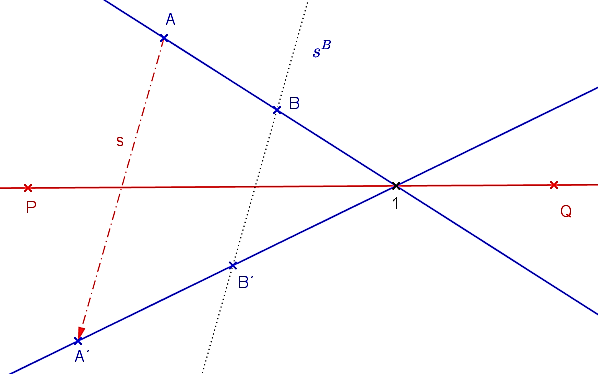
Obr. Afinita
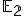 dve rôznobežné priamky
dve rôznobežné priamky 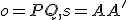 . Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie
. Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie 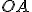 s vlastnosťami
s vlastnosťami
- Obrazom ľubovoľného bodu
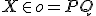 je ten istý bod
je ten istý bod 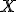 , priamka
, priamka 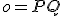 je bodovo samodružná..
je bodovo samodružná.. - Obrazom ľubovoľného bodu
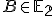 je bod
je bod 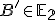 , ktorý leží na priamke
, ktorý leží na priamke 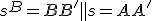 .
. - Obrazom priamky
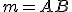 je priamka
je priamka 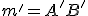 , pričom bod
, pričom bod 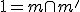 je samodružný. V prípade
rovnobežnosti
je samodružný. V prípade
rovnobežnosti 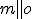 je tiež
je tiež 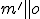 (bod 1 je nevlastný).
(bod 1 je nevlastný). - Obrazom priamky rovnobežnej s priamkou
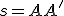 je tá istá priamka, priamka je samodružná.
je tá istá priamka, priamka je samodružná. - Takéto zobrazenie je zrejme bijektívne zobrazenie euklidovskej roviny. Budeme ho nazývať osová afinita v rovine.
Obr. Afinita
Vlastnosti.
- osová afinita je jednoznačne určená priakou
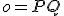 a dvojicou odpovedajúcich si bodov
a dvojicou odpovedajúcich si bodov 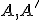 ,
, - priamku
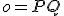 nazývame os afinity a priamku
nazývame os afinity a priamku 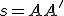 nazývame smer afinity,
nazývame smer afinity, - osová afinita zachováva incidenciu, rovnobežnosť a deliaci pomer troch kolineárnych bodov. Dôkaz je založený na vlastnosti podobných trojuholníkov. Pozrite si prácu [PLICH].
Osovú afinitu môžeme využiť aj pri dôkazoch niektorých vlastností všeobecných trojuholníkov. Stačí ak dokážeme určiť osovú afinitu, v ktorej sa daný všeobecný trojuholník zobrazí na rovnostraný trojuholník. Keďže osová afinita zachováva incidenciu a deliaci pomer (špeciálne stred úsečky sa zobrazí do stredu úsečky), tak napríklad vlastnosť ťažníc stačí dokázať len pre rovnostranný trojuholník.
Uvedieme konštrukciu ako takúto osová afinitu určuíť.
Uvedieme konštrukciu ako takúto osová afinitu určuíť.
Cvičenie.
Určte OA tak, aby sa všeobecný trojuholník zobrazil do rovnostranného trojuholníka
zobrazil do rovnostranného trojuholníka 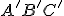 . Riešenie nájdete Tu.
. Riešenie nájdete Tu.
Určte OA tak, aby sa všeobecný trojuholník
 zobrazil do rovnostranného trojuholníka
zobrazil do rovnostranného trojuholníka 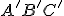 . Riešenie nájdete Tu.
. Riešenie nájdete Tu.
Riešené príklady.
Osová afinita je daná osou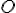 a dvojicou odpovedajúcich bodov
a dvojicou odpovedajúcich bodov 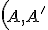
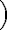 .
Zostrojte bod
.
Zostrojte bod 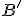 , ktorý je obrazom daného bodu
, ktorý je obrazom daného bodu 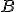 . Nech
. Nech 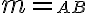 je priamka určená bodmi
je priamka určená bodmi 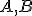 . Uvažujme dva prípady:
. Uvažujme dva prípady:
Osová afinita je daná osou
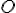 a dvojicou odpovedajúcich bodov
a dvojicou odpovedajúcich bodov 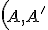
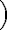 .
Zostrojte bod
.
Zostrojte bod 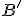 , ktorý je obrazom daného bodu
, ktorý je obrazom daného bodu 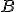 . Nech
. Nech 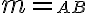 je priamka určená bodmi
je priamka určená bodmi 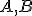 . Uvažujme dva prípady:
. Uvažujme dva prípady:
- Priamka
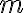 je rôznobežná s osou
je rôznobežná s osou  , riešenie Tu.
, riešenie Tu. - Ak priamka
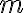 je rovnobežná s osou
je rovnobežná s osou  tak použijeme konštrukciu:
tak použijeme konštrukciu:
- zvoľme si vhodnú priamku
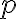 prechádzajúcu bodom
prechádzajúcu bodom 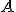 , ktorá nie je rovnobežná s osou
, ktorá nie je rovnobežná s osou 
- na priamke
 si zvoľme bod
si zvoľme bod 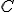 tak, aby priamka
tak, aby priamka 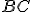 nebola rovnobežná s osou
nebola rovnobežná s osou 
- obrazom priamky
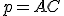 je priamka
je priamka 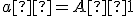 , obraz
, obraz 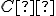 bodu
bodu 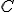 musí ležať na priamke
musí ležať na priamke 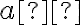
- bodmi
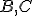 je určená priamka
je určená priamka 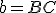 , obrazom priamky
, obrazom priamky 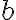 je priamka
je priamka 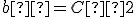
- obraz
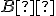 bodu
bodu 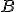 musí ležať na priamke
musí ležať na priamke 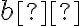 , riešenie
Tu.
, riešenie
Tu.
- zvoľme si vhodnú priamku
Veta.
Obraz kružnice v osovej afinite je elipsa (dôkaz je jednoduchý ak využijeme metódy analytickej geometrie).
Obraz kružnice v osovej afinite je elipsa (dôkaz je jednoduchý ak využijeme metódy analytickej geometrie).
Na zostrojenie takejto elipsu môžeme využiť dva spôsoby.
- Priama konštrukcia hlavnej a vedľajšej poloosi.
Nájdením združených priemerov elipsy. Využijeme skutočnosť, že v kružnici združené priemery sú také priemery, ktoré sú vzájomne kolmé. (Priemery elipsy resp. kružnice sa nazývajú združené, ak sú dotyčnice v krajných bodoch jedného priemeru rovnobežné s druhým priemerom a naopak.) - Nepriamo pomocou Rytzovej konštrukcie.
V kružnici zvolíme dva ľubovoľné na seba kolmé priemery KL, MN a nájdeme ich obrazy K'L', M'N'. Osová afinita zachováva rovnobežnosť a deliaci pomer. Preto tvoria úsečky K'L', M'N' združené priemery elipsy. Ak poznáme dva združené priemery elipsy, využijeme na nájdenie hlavnej a vedľajšej osi Rytzovu konštrukciu. Stiahnite si Rytzovu konštrukciu Tu a pozrite si prácu [PLI].
Poznámka.
Vzťah osovej afinity v euklidovskej rovine si môžeme predstaviť aj ako kolmý priemet priestorovej afinity. Uvedieme definíciu osovej afinity medzi dvoma rôznobežnými rovinami v euklidovskom priestore z práce [DRA]. Pozrite si dynamický obrázok "Priestorová afinita".
Vzťah osovej afinity v euklidovskej rovine si môžeme predstaviť aj ako kolmý priemet priestorovej afinity. Uvedieme definíciu osovej afinity medzi dvoma rôznobežnými rovinami v euklidovskom priestore z práce [DRA]. Pozrite si dynamický obrázok "Priestorová afinita".
Definícia.
Uvažujme dve rôznobežné roviny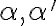 a ich priesečnicu označme
a ich priesečnicu označme 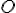 . Zvoľme ďalej smer
. Zvoľme ďalej smer 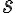 , ktorý je rôznobežný s oboma rovinami
, ktorý je rôznobežný s oboma rovinami
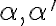 . Potom priradíme navzájom body a priamky roviny
. Potom priradíme navzájom body a priamky roviny  bodom a priamkam roviny
bodom a priamkam roviny 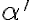 tak, že platí:
tak, že platí:
Uvažujme dve rôznobežné roviny
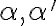 a ich priesečnicu označme
a ich priesečnicu označme 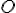 . Zvoľme ďalej smer
. Zvoľme ďalej smer 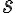 , ktorý je rôznobežný s oboma rovinami
, ktorý je rôznobežný s oboma rovinami
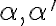 . Potom priradíme navzájom body a priamky roviny
. Potom priradíme navzájom body a priamky roviny  bodom a priamkam roviny
bodom a priamkam roviny 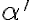 tak, že platí:
tak, že platí:
- Osovú afinitu medzi dvoma rôznobežnými rovinami s výhodou využívame pri rezoch rovnobežnostena.
- Porovnajme vlastnosti osovej afinity s rezom hranola, obrázok "Rez hranola (obrázok je prevzatý s práce [PLI]).
- Rovina
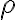 zodpovedá rovine rezu, rovina
zodpovedá rovine rezu, rovina 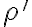 zodpovedá rovine dolnej podstavy. Smer afinity s zodpovedá smeru hrán, napríklad
zodpovedá rovine dolnej podstavy. Smer afinity s zodpovedá smeru hrán, napríklad 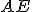 . Zodpovedajúce si body sú napríklad body
. Zodpovedajúce si body sú napríklad body 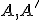 . Os
. Os 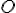 je priesečnica rovín
je priesečnica rovín 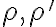 a zodpovedá priesečnici roviny podstavy a roviny rezu.
a zodpovedá priesečnici roviny podstavy a roviny rezu.
Obr. Rez hranola
