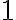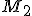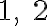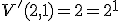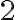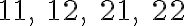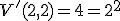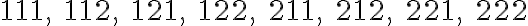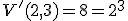Kombinatorika
Permutácie a variácie
Variácie s opakovaním
Z prvkov množiny  je možné vytvoriť skupiny po
je možné vytvoriť skupiny po  prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny
prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny  . Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
. Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
 je možné vytvoriť skupiny po
je možné vytvoriť skupiny po  prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny
prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny  . Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
. Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
Definícia.
Usporiadaná -tica prvkov množiny
-tica prvkov množiny 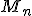 sa nazýva
sa nazýva  -variácia s opakovaním množiny
-variácia s opakovaním množiny 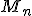 .
Počet všetkých
.
Počet všetkých  -variácií s opakovaním množiny
-variácií s opakovaním množiny 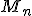 budeme označovať symbolom
budeme označovať symbolom 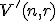 .
.
Usporiadaná
 -tica prvkov množiny
-tica prvkov množiny 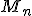 sa nazýva
sa nazýva  -variácia s opakovaním množiny
-variácia s opakovaním množiny 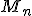 .
Počet všetkých
.
Počet všetkých  -variácií s opakovaním množiny
-variácií s opakovaním množiny 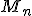 budeme označovať symbolom
budeme označovať symbolom 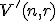 .
.
Príklad.
Utvorte všetky 3-variácie s opakovaním množiny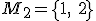 .
.
Riešenie.
Postupne vytvárajme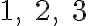 -variácie s opakovaním množiny
-variácie s opakovaním množiny 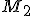 .
.
Utvorte všetky 3-variácie s opakovaním množiny
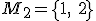 .
.
Riešenie.
Postupne vytvárajme
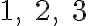 -variácie s opakovaním množiny
-variácie s opakovaním množiny 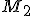 .
.
Veta.
Pre počet všetkých -variácií s opakovaním množiny
-variácií s opakovaním množiny 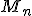 platí vzťah
platí vzťah 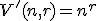
Dôkaz.
Použitím matematickej indukcie. Pre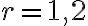 je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre
je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre  . Teda
. Teda
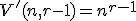
Všetky usporiadané -tice s opakovaním množiny
-tice s opakovaním množiny 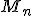 možno vytvoriť z
možno vytvoriť z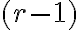 -tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny
-tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny 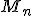 . Preto z každej
. Preto z každej 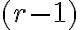 -tice získame
-tice získame  rôznych
rôznych  -tíc. Využitím indukčného predpokladu dostaneme
-tíc. Využitím indukčného predpokladu dostaneme
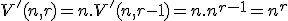 .
.
Pre počet všetkých
 -variácií s opakovaním množiny
-variácií s opakovaním množiny 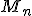 platí vzťah
platí vzťah 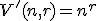
Dôkaz.
Použitím matematickej indukcie. Pre
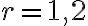 je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre
je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre  . Teda
. Teda
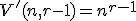
Všetky usporiadané
 -tice s opakovaním množiny
-tice s opakovaním množiny 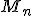 možno vytvoriť z
možno vytvoriť z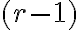 -tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny
-tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny 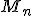 . Preto z každej
. Preto z každej 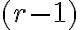 -tice získame
-tice získame  rôznych
rôznych  -tíc. Využitím indukčného predpokladu dostaneme
-tíc. Využitím indukčného predpokladu dostaneme
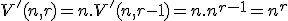 .
.
Urobte dôkaz využitím kombinačného pravidla súčinu.