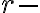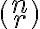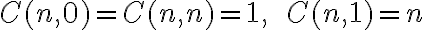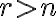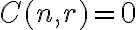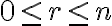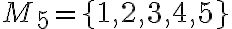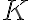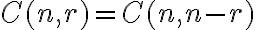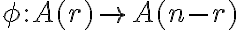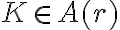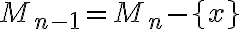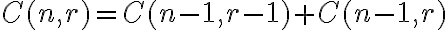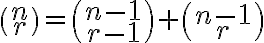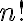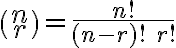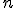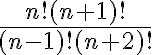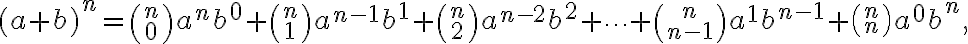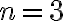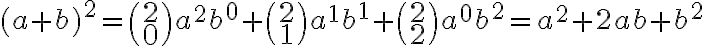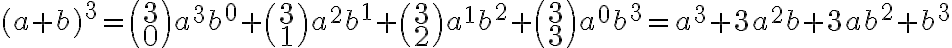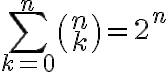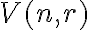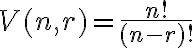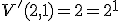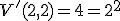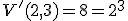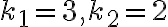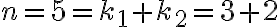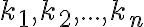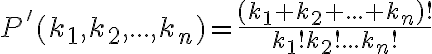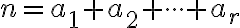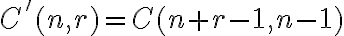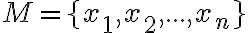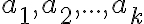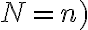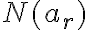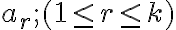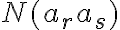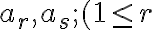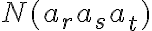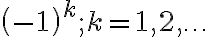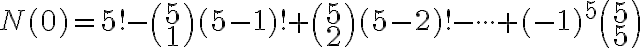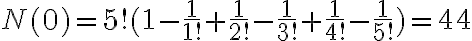Kombinatorika
| Site: | Virtuálna Univerzita Mateja Bela |
| Course: | Kombinatorika |
| Book: | Kombinatorika |
| Printed by: | Guest user |
| Date: | Wednesday, 3 July 2024, 11:42 AM |
Úvod
Predkladaný text vychádza z práce významného slovenského matematika prof. RNDr. Štefana Známa, DrSc. Nami upravený učebný text rozširuje poznatky z kombinatoriky na stredných školách. Celý text vo formáte WORD si môžete stiahnuť Tu.
významného slovenského matematika prof. RNDr. Štefana Známa, DrSc. Nami upravený učebný text rozširuje poznatky z kombinatoriky na stredných školách. Celý text vo formáte WORD si môžete stiahnuť Tu.
 významného slovenského matematika prof. RNDr. Štefana Známa, DrSc. Nami upravený učebný text rozširuje poznatky z kombinatoriky na stredných školách. Celý text vo formáte WORD si môžete stiahnuť Tu.
významného slovenského matematika prof. RNDr. Štefana Známa, DrSc. Nami upravený učebný text rozširuje poznatky z kombinatoriky na stredných školách. Celý text vo formáte WORD si môžete stiahnuť Tu.
Kombinatorika je obor matematiky, ktorý sa zaoberá skupinami prvkov množín s definovanou vnútornou štruktúrou.
Skupiny prvkov vo všeobecnosti rozdelíme do štyroch základných tried
|
Prvky sa neopakujú
Prvky sa môžu opakovať
|
Nezáleží na poradí prvkov
Kombinácie bez opakovania
Kombinácie s opakovaním
|
Záleží na poradí prvkov
Variácie bez opakovania
Variácie s opakovaním
|
Poradie: V prípade, že záleží na poradí prvkov, hovoríme o usporiadaných skupinách - variáciách. Ak na poradí nezáleží, hovoríme o neusporiadaných skupinách - kombináciách.
Opakovanie: V prípade, že každý prvok sa vyskytuje najviac jedenkrát hovoríme o skupinách bez opakovania. Ak sa môže ľubovoľný prvok vyskytnúť viac krát, hovoríme o skupinách s opakovaním.
Opakovanie: V prípade, že každý prvok sa vyskytuje najviac jedenkrát hovoríme o skupinách bez opakovania. Ak sa môže ľubovoľný prvok vyskytnúť viac krát, hovoríme o skupinách s opakovaním.
Uveďte príklady skupín prvkov, ktoré budú reprezentovať každú zo štyroch základných tried.
Pri určovaní počtu skupín prvkov množín bežne využívame kombinatorické pravidlo súčinu a súčtu. Viac v práci [Farská, 2007]2) Tu.
________________________________________________________________________________________
1) Znám, Š.: Kombinatorika a teória grafov. Vysokoškolský učebný text, UK Bratislava, 1978
2) Farská, J.: Výuka kombinatoriky na střední škole s využitím webových stránek. Diplomová práce, MFF UK Praha (2007). Dostupné Tu.
2) Stodolová, K.: Klasické kombinatorické úlohy. Diplomová práce, MFF UK Praha (2012). Dostupné Tu
1) Znám, Š.: Kombinatorika a teória grafov. Vysokoškolský učebný text, UK Bratislava, 1978
2) Farská, J.: Výuka kombinatoriky na střední škole s využitím webových stránek. Diplomová práce, MFF UK Praha (2007). Dostupné Tu.
2) Stodolová, K.: Klasické kombinatorické úlohy. Diplomová práce, MFF UK Praha (2012). Dostupné Tu
Kombinácie bez opakovania
Ak  je prirodzene číslo, symbolom
je prirodzene číslo, symbolom  označujeme akúkoľvek
označujeme akúkoľvek  -
prvkovú množinu. V ďalšom spravidla budeme predpokladať, že prvkami množiny
-
prvkovú množinu. V ďalšom spravidla budeme predpokladať, že prvkami množiny  sú čísla
sú čísla 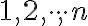 (niekedy
to zase budú písmená
(niekedy
to zase budú písmená 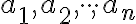 .
.
 je prirodzene číslo, symbolom
je prirodzene číslo, symbolom  označujeme akúkoľvek
označujeme akúkoľvek  -
prvkovú množinu. V ďalšom spravidla budeme predpokladať, že prvkami množiny
-
prvkovú množinu. V ďalšom spravidla budeme predpokladať, že prvkami množiny  sú čísla
sú čísla 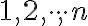 (niekedy
to zase budú písmená
(niekedy
to zase budú písmená 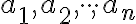 .
.
Každá podmnožina 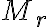 množiny
množiny  sa nazýva kombinácia množiny
sa nazýva kombinácia množiny
 . Ak
. Ak 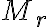 pozostáva z
pozostáva z  prvkov, tak ju
prvkov, tak ju
nazývame -kombináciou.
-kombináciou.
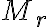 množiny
množiny  sa nazýva kombinácia množiny
sa nazýva kombinácia množiny
 . Ak
. Ak 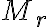 pozostáva z
pozostáva z  prvkov, tak ju
prvkov, tak ju
nazývame
 -kombináciou.
-kombináciou.
Pri tvorení kombinácií nezáleží na poradí prvkov! Napríklad trojice 123 a 321 predstavujú tú istú kombináciu. Prvky v kombinácii obyčajne usporadúvame v tom poradí ako v základnej množine  .
.
 .
.
Príklad kombinácií
Riešenie.
-
Zrejme, každá množina má jedinú
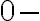 kombináciu (je ňou prázdna množina ∅).
kombináciu (je ňou prázdna množina ∅). -
Podľa definície
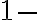 kombinácie sú všetky jednoprvkové podmnožiny množiny
kombinácie sú všetky jednoprvkové podmnožiny množiny 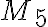 . Sú to množiny:
. Sú to množiny: 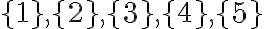 . Pre kombinácie nepoužívame tento množinový zápis, ale ich píšeme jednoducho:
. Pre kombinácie nepoužívame tento množinový zápis, ale ich píšeme jednoducho: 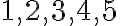 . Ich počet je 5.
. Ich počet je 5.
-
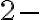 kombinácie utvoríme tak, že ku každej
kombinácie utvoríme tak, že ku každej 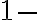 kombinácii a pripojíme vpravo po jednom všetky prvky, ktoré sa v množine
kombinácii a pripojíme vpravo po jednom všetky prvky, ktoré sa v množine 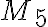 nachádzajú vpravo od
nachádzajú vpravo od  . Postup tvorby Tu. Ich počet je 10.
. Postup tvorby Tu. Ich počet je 10. -
Obdobne získame všetky
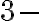 kombinácie. Ku každej
kombinácie. Ku každej 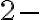 kombinácii
kombinácii 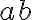 pripojíme po jednom každý prvok, ktorý leží v
pripojíme po jednom každý prvok, ktorý leží v 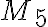 vpravo od
vpravo od  (ak taký prvok existuje) . Dostaneme tieto
(ak taký prvok existuje) . Dostaneme tieto 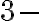 kombinácie:
kombinácie: 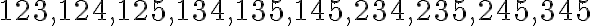 . Ich počet je 10.
. Ich počet je 10. -
Podobne postupujeme pri tvorbe
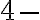 kombinácií. Ich počet je 5 a sú to
kombinácií. Ich počet je 5 a sú to 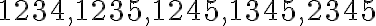 .
. -
Existuje len jedna
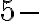 kombinácia
kombinácia 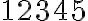 .
.
-
Zrejme, množina
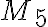 nemá nijakú
nemá nijakú 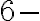 kombináciu.
kombináciu.
Doplnková kombinácia
Dôkaz tvrdenia:
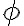 je bijekcia, preto množiny
je bijekcia, preto množiny 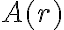 a
a 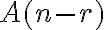 majú
rovnaký počet prvkov. Tým je dôkaz ukončený.
majú
rovnaký počet prvkov. Tým je dôkaz ukončený.
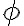 je bijekcia, preto množiny
je bijekcia, preto množiny 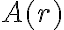 a
a 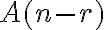 majú
rovnaký počet prvkov. Tým je dôkaz ukončený.
majú
rovnaký počet prvkov. Tým je dôkaz ukončený.
Príklad.
Pri výťahu, do ktorého môžu nastúpiť najviac tri osoby, stojí 5 osôb. Označme je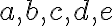 . Zostavte všetky trojice osôb, ktoré môžu nastúpiť do výťahu.
. Zostavte všetky trojice osôb, ktoré môžu nastúpiť do výťahu.
Riešenie:
 Otvorte si zadanie Tu
Otvorte si zadanie Tu
Pri výťahu, do ktorého môžu nastúpiť najviac tri osoby, stojí 5 osôb. Označme je
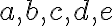 . Zostavte všetky trojice osôb, ktoré môžu nastúpiť do výťahu.
. Zostavte všetky trojice osôb, ktoré môžu nastúpiť do výťahu.
Riešenie:
Pevný prvok - počet kombinácií
Tvrdenie. Nech  je pevný prvok množiny
je pevný prvok množiny  a nech
a nech 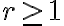 . Počet
. Počet 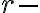 kombinácií množiny
kombinácií množiny  , ktoré
, ktoré
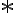 prvok
prvok  obsahujú sa rovná
obsahujú sa rovná 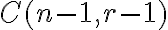
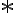 prvok
prvok  neobsahujú sa rovná
neobsahujú sa rovná 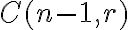
 je pevný prvok množiny
je pevný prvok množiny  a nech
a nech 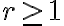 . Počet
. Počet 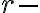 kombinácií množiny
kombinácií množiny  , ktoré
, ktoré
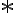 prvok
prvok  obsahujú sa rovná
obsahujú sa rovná 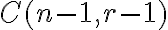
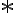 prvok
prvok  neobsahujú sa rovná
neobsahujú sa rovná 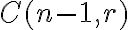
Dôkaz tvrdenia:


Poznámka.
Rovnosť uvedená v dôsledku je vlastne rekurentným vzťahom. Počet -kombinácií
-kombinácií  -prvkovej množiny je vyjadrený pomocou počtu kombinácií
-prvkovej množiny je vyjadrený pomocou počtu kombinácií 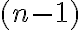 -prvkovej množiny. Stačí začať s 1-prvkovou množinou, pre ktorú platí:
-prvkovej množiny. Stačí začať s 1-prvkovou množinou, pre ktorú platí:
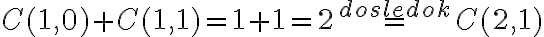
a postupne určiť počet kombinácií vyššieho rádu. Toto nás privádza k myšlienke pokúsiť sa o explicitné vyjadrenie kombinačných čísel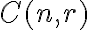 .
.
Rovnosť uvedená v dôsledku je vlastne rekurentným vzťahom. Počet
 -kombinácií
-kombinácií  -prvkovej množiny je vyjadrený pomocou počtu kombinácií
-prvkovej množiny je vyjadrený pomocou počtu kombinácií 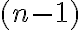 -prvkovej množiny. Stačí začať s 1-prvkovou množinou, pre ktorú platí:
-prvkovej množiny. Stačí začať s 1-prvkovou množinou, pre ktorú platí:
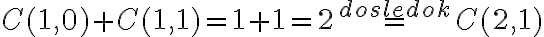
a postupne určiť počet kombinácií vyššieho rádu. Toto nás privádza k myšlienke pokúsiť sa o explicitné vyjadrenie kombinačných čísel
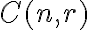 .
.
Pascalov trojuholník
Pre 1-prvkovú množinu zrejme platí:
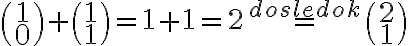
opäť použijeme tvrdenie uvedené v dôsledku teraz pre 2-prvkovú množinu a dostaneme:
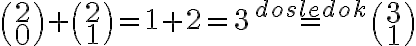
a zároveň pre 2-prvkovú množinu tiež platí:
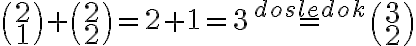 .
.
Takto by sme mohli postupovať pre väčšie hodnoty . Napríklad už poznáme hodnoty
. Napríklad už poznáme hodnoty
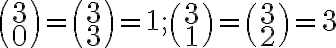
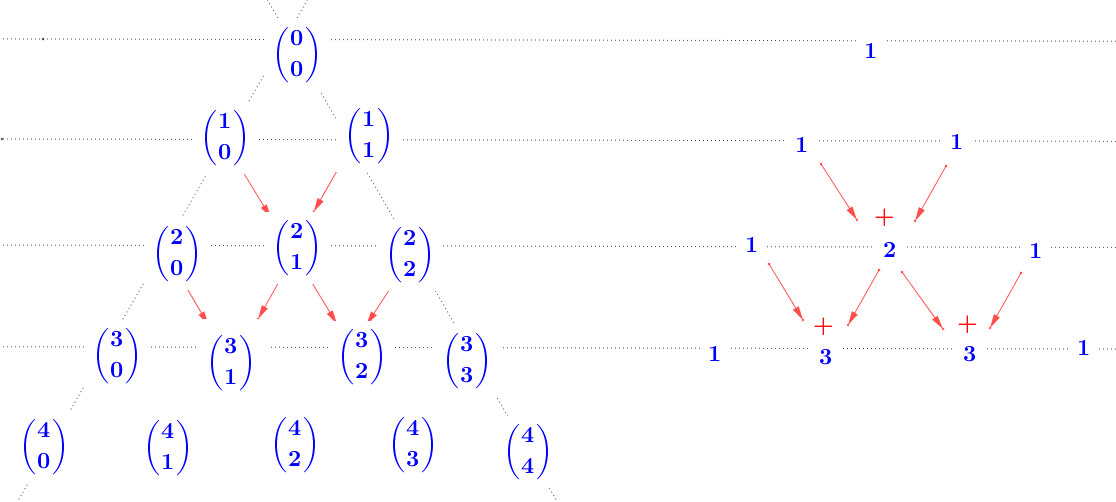
preto ľahko spočítame hodnoty pre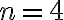 . Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
. Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
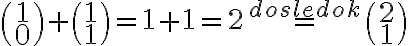
opäť použijeme tvrdenie uvedené v dôsledku teraz pre 2-prvkovú množinu a dostaneme:
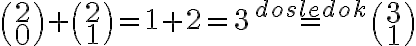
a zároveň pre 2-prvkovú množinu tiež platí:
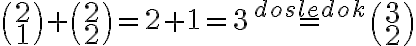 .
.Takto by sme mohli postupovať pre väčšie hodnoty
 . Napríklad už poznáme hodnoty
. Napríklad už poznáme hodnoty
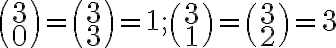
preto ľahko spočítame hodnoty pre
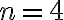 . Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
. Ak tieto výpočty budeme zapisovať do trojuholníkovej schémy, tak dostaneme známy Pascalov trojuholník pre kombinačné čísla.
Kombinačné číslo
Teda 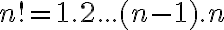 je prirodzené číslo, ktoré skrátene nazývame
je prirodzené číslo, ktoré skrátene nazývame  - faktoriál. Symbol
- faktoriál. Symbol 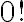 definitoricky bude predstavovať číslo rovné
definitoricky bude predstavovať číslo rovné 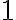 .
.
V nasledujúcom texte budeme pre kombinačné číslo používať označenie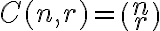
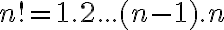 je prirodzené číslo, ktoré skrátene nazývame
je prirodzené číslo, ktoré skrátene nazývame  - faktoriál. Symbol
- faktoriál. Symbol 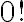 definitoricky bude predstavovať číslo rovné
definitoricky bude predstavovať číslo rovné 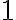 .
.
V nasledujúcom texte budeme pre kombinačné číslo používať označenie
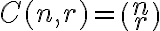
Dôkaz.
Všimnite si zaujímavý fakt: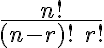 je celé číslo pre ľubovoľné
je celé číslo pre ľubovoľné
 a
a
 ,
,
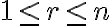 .
.
-
Pre
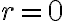 pravdivosť tvrdenia je zrejmá.
pravdivosť tvrdenia je zrejmá. - Predpokladajme, že platí
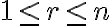 . Budeme dokazovať indukciou vzhľadom na číslo
. Budeme dokazovať indukciou vzhľadom na číslo
 .
. - Overenie pravdivosti tvrdenia v prípade
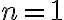 prenechávame na čitateľa.
prenechávame na čitateľa. - Predpokladajme (indukčný predpoklad), že tvrdenie platí pre
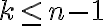 .
.
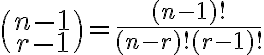
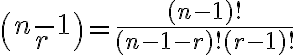
Dokážeme, že platí aj pre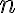 .
. -
Na základe predchádzajúceho dôsledku platí rovnosť:
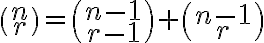 na základe indukčného predpokladu môžeme rovnosť ďalej upraviť: applet Tu
na základe indukčného predpokladu môžeme rovnosť ďalej upraviť: applet Tu
Všimnite si zaujímavý fakt:
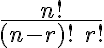 je celé číslo pre ľubovoľné
je celé číslo pre ľubovoľné
 a
a
 ,
,
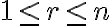 .
.Binomická veta
Predpokladáme, že študentom sú známe vzorce pre mocniny dvojčlena 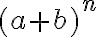 ak
ak 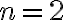 resp. pre
resp. pre 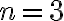 . Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
. Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
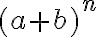 ak
ak 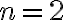 resp. pre
resp. pre 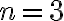 . Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
. Pre umocňovanie s vyšším exponentom odvodíme vzorce pomocou tzv. binomickej vety, ktorú teraz dokážeme.
Dôkaz vety
Pri dôkaze binomickej vety vychádzame z toho, že v súčine
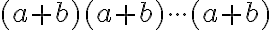
člen
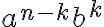
dostaneme tak, že z dvojčlenov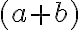 vyberieme
vyberieme 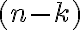 -krát reálne číslo
-krát reálne číslo  a potom
a potom  -krát reálne číslo
-krát reálne číslo  . To je možné práve
. To je možné práve
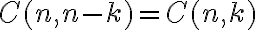
spôsobmi, čím je dôkaz ukončený. Dôkaz binomickej vety môžeme urobiť aj pomocou úplnej matematickej indukcie.
Pri dôkaze binomickej vety vychádzame z toho, že v súčine
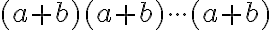
člen
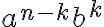
dostaneme tak, že z dvojčlenov
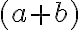 vyberieme
vyberieme 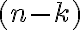 -krát reálne číslo
-krát reálne číslo  a potom
a potom  -krát reálne číslo
-krát reálne číslo  . To je možné práve
. To je možné práve
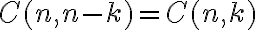
spôsobmi, čím je dôkaz ukončený. Dôkaz binomickej vety môžeme urobiť aj pomocou úplnej matematickej indukcie.
Poznámky
Permutácie a variácie
Definícia.
Nech označujeme akúkoľvek
označujeme akúkoľvek  -prvkovú množinu. Permutáciou množiny
-prvkovú množinu. Permutáciou množiny
 nazývame jej bijektívne zobrazenie na seba.
nazývame jej bijektívne zobrazenie na seba.
Nech
 označujeme akúkoľvek
označujeme akúkoľvek  -prvkovú množinu. Permutáciou množiny
-prvkovú množinu. Permutáciou množiny
 nazývame jej bijektívne zobrazenie na seba.
nazývame jej bijektívne zobrazenie na seba.
Napríklad zobrazenie
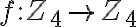 dané predpisom:
dané predpisom:
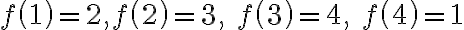
je bijekcia množiny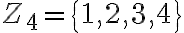 na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
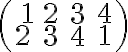
alebo jednoducho ako postupnosť
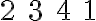 .
.
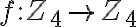 dané predpisom:
dané predpisom:
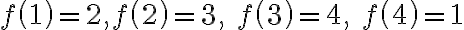
je bijekcia množiny
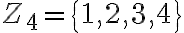 na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
na seba. Takúto permutáciu budeme symbolicky zapisovať pomocou matice
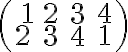
alebo jednoducho ako postupnosť
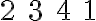 .
.
Príklad.
Nájdite všetky permutácie ľubovoľnej štvorprvkovej množiny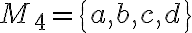 .
.
Riešenie.
Nech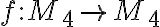 je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
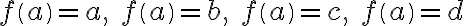 .
.
Ak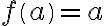 , tak obraz prvku
, tak obraz prvku  môže nadobúdať tri rôzne hodnoty
môže nadobúdať tri rôzne hodnoty
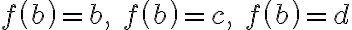
Ak už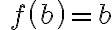 , tak obraz prvku
, tak obraz prvku  môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne

Pre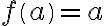 sme dostali permutácie
sme dostali permutácie 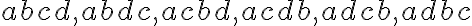 . Podobne budeme postupovať pre
. Podobne budeme postupovať pre 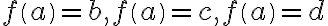 . Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.
. Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.

Na základe postupu použitého v predchádzajúcom príklade môžeme dokázať tvrdenie uvedené vo vete 9, v ktorej je uvedený vzorec pre určenie počtu všetkých permutácii ľubovoľnej množiny .
.
Nájdite všetky permutácie ľubovoľnej štvorprvkovej množiny
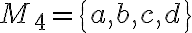 .
.
Riešenie.
Nech
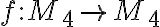 je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
je bijekcia. Potom obraz prvku a môže nadobúdať štyri rôzne hodnoty:
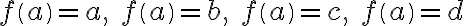 .
.
Ak
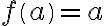 , tak obraz prvku
, tak obraz prvku  môže nadobúdať tri rôzne hodnoty
môže nadobúdať tri rôzne hodnoty
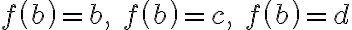
Ak už
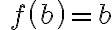 , tak obraz prvku
, tak obraz prvku  môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
môže nadobúdať dve rôzne hodnoty atď. Schematicky to môžeme znázorniť nasledovne
Pre
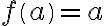 sme dostali permutácie
sme dostali permutácie 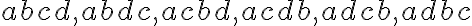 . Podobne budeme postupovať pre
. Podobne budeme postupovať pre 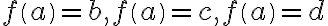 . Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.
. Všetky permutácie prehľadne zapíšeme pomocou nasledujúcej tabuľky.
Na základe postupu použitého v predchádzajúcom príklade môžeme dokázať tvrdenie uvedené vo vete 9, v ktorej je uvedený vzorec pre určenie počtu všetkých permutácii ľubovoľnej množiny
 .
.
Tvrdenie. Pre počet permutácií
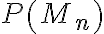 množiny
množiny
 platí vzťah
platí vzťah 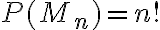
Dôkaz tohto tvrdenia môžeme ľahko urobiť ak využijeme kombinatorické pravidlo súčinu.
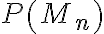 množiny
množiny
 platí vzťah
platí vzťah 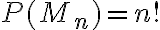
Dôkaz tohto tvrdenia môžeme ľahko urobiť ak využijeme kombinatorické pravidlo súčinu.
Kombinatorické pravidlo súčinu
Kombinatorické pravidlo súčinu
Nech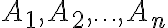 sú množiny majúce po rade
sú množiny majúce po rade 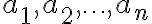 prvkov. Potom počet usporiadaných
prvkov. Potom počet usporiadaných  -tíc, ktorých prvý prvok je z množiny
-tíc, ktorých prvý prvok je z množiny
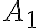 , druhý z množiny
, druhý z množiny
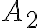 a
a  -tý z množiny
-tý z množiny
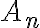 je rovný súčinu
je rovný súčinu 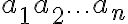 .
.
Dôkaz prenechávame na čitateľa. Odporúčame použiť matematickú indukciu vzhľadom na počet množín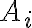 .
.
Nech
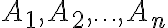 sú množiny majúce po rade
sú množiny majúce po rade 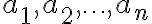 prvkov. Potom počet usporiadaných
prvkov. Potom počet usporiadaných  -tíc, ktorých prvý prvok je z množiny
-tíc, ktorých prvý prvok je z množiny
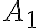 , druhý z množiny
, druhý z množiny
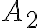 a
a  -tý z množiny
-tý z množiny
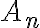 je rovný súčinu
je rovný súčinu 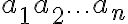 .
.
Dôkaz prenechávame na čitateľa. Odporúčame použiť matematickú indukciu vzhľadom na počet množín
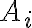 .
.
Príklad 1.
V košíku je 12 jabĺk a 10 hrušiek. Peter si má z neho vybrať buď jablko, alebo hrušku tak, aby Viera, ktorá si po ňom vyberie jedno jablko a jednu hrušku, mala čo najväčšiu možnosť výberu. Určte, čo si má vybrať Peter.
Riešenie.
Peter má pri výbere dve možnosti. Buď si vyberie jablko, alebo hrušku. Otvorte si tabuľu Tu.
V košíku je 12 jabĺk a 10 hrušiek. Peter si má z neho vybrať buď jablko, alebo hrušku tak, aby Viera, ktorá si po ňom vyberie jedno jablko a jednu hrušku, mala čo najväčšiu možnosť výberu. Určte, čo si má vybrať Peter.
Riešenie.
Peter má pri výbere dve možnosti. Buď si vyberie jablko, alebo hrušku. Otvorte si tabuľu Tu.
Príklad 2.
Karol má červenú, modrú, žltú a zelenú kravatu. Ďalej má červenú, modrú a zelenú košeľu. Koľkými spôsobmi si môže obliecť oboje, aby nemal košeľu a kravatu rovnakej farby?
Riešenie.
Najskôr spočítajte koľko možností je nevhodných - rovnakej farby kravata aj košeľa. Potom použite kombinatorické pravidlo súčinu. Otvorte si tabuľu Tu.
Karol má červenú, modrú, žltú a zelenú kravatu. Ďalej má červenú, modrú a zelenú košeľu. Koľkými spôsobmi si môže obliecť oboje, aby nemal košeľu a kravatu rovnakej farby?
Riešenie.
Najskôr spočítajte koľko možností je nevhodných - rovnakej farby kravata aj košeľa. Potom použite kombinatorické pravidlo súčinu. Otvorte si tabuľu Tu.
Cvičenie 1..
Koľko rôznych usporiadaných dvojíc čísel môžeme dostať, keď hodíme dvakrát kockou s jedným až šiestimi okami na jednotlivých stenách?
Riešenie
V prvom hode môže padnúť jedno zo šiestich čísel. To znamená, že máme 6 možností (6 rôznych hodnôt na vrchnej strane kocky).
Ku každej hodnote môže v druhom hode opäť padnúť jedno zo šiestich čísel, tj opäť 6 možností.
Počet rôznych dvojíc je teda 6 x 6 = 36." Tabuľa
Riešenie
V prvom hode môže padnúť jedno zo šiestich čísel. To znamená, že máme 6 možností (6 rôznych hodnôt na vrchnej strane kocky).
Ku každej hodnote môže v druhom hode opäť padnúť jedno zo šiestich čísel, tj opäť 6 možností.
Počet rôznych dvojíc je teda 6 x 6 = 36." Tabuľa
Cvičenie 2..
Určite počet všetkých trojciferných prirodzených čísel,
a) v ktorých dekadickom zápise sa každá číslica vyskytuje najviac raz;
b) v ktorých dekadickom zápise sa nejaká číslica vyskytuje aspoň dvakrát
Riešenie
a)
- možnosti pre prvú číslicu: 1 až 9 → 9 možností;
- možnosti pre druhú číslicu: 0 až 9, ale bez tej číslice, ktorá bola vybraná pre prvú číslicu → 10 − 1 = 9 možností;
- možnosti pre tretiu číslicu: 0 až 9, ale bez číslic, ktoré boli vybrané pre prvú a druhú číslicu → 10 − 2 = 8 možností.
Podľa kombinatorického pravidla súčinu je teda celkom 9 ⋅ 9 ⋅ 8 = 648 takýchto čísel.
b)
Všetkých trojciferných čísel je 900 (čísla 100 až 999), z toho čísel, v ktorých dekadickom zápise sa každá číslica vyskytuje najviac raz, je 648 – viď prípad a). Zostáva teda 900-648 čísel, v ktorých dekadickom zápise sa nejaká číslica opakuje aspoň dvakrát."
a) v ktorých dekadickom zápise sa každá číslica vyskytuje najviac raz;
b) v ktorých dekadickom zápise sa nejaká číslica vyskytuje aspoň dvakrát
Riešenie
a)
- možnosti pre prvú číslicu: 1 až 9 → 9 možností;
- možnosti pre druhú číslicu: 0 až 9, ale bez tej číslice, ktorá bola vybraná pre prvú číslicu → 10 − 1 = 9 možností;
- možnosti pre tretiu číslicu: 0 až 9, ale bez číslic, ktoré boli vybrané pre prvú a druhú číslicu → 10 − 2 = 8 možností.
Podľa kombinatorického pravidla súčinu je teda celkom 9 ⋅ 9 ⋅ 8 = 648 takýchto čísel.
b)
Všetkých trojciferných čísel je 900 (čísla 100 až 999), z toho čísel, v ktorých dekadickom zápise sa každá číslica vyskytuje najviac raz, je 648 – viď prípad a). Zostáva teda 900-648 čísel, v ktorých dekadickom zápise sa nejaká číslica opakuje aspoň dvakrát."
Úlohy
Úloha 1.
Koľko trojciferných čísel môžeme vytvoriť z číslic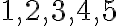 , ak sa žiadna číslica neopakuje?
, ak sa žiadna číslica neopakuje?
Riešenie
Výsledok: V(5,3) = 60
Koľko trojciferných čísel môžeme vytvoriť z číslic
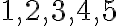 , ak sa žiadna číslica neopakuje?
, ak sa žiadna číslica neopakuje?
Riešenie
Výsledok: V(5,3) = 60
Úloha 2.
Koľko rôznych jedno až štvorciferných čísel môžeme vytvoriť z cifier 0, 1, 2, 3?
Riešenie
Keby medzi ciframi nebola nula, tak počet všetkých jedno až štvorciferných čísel by bol súčet čísel
V(4,1)+V(4,2)+V(4,3)+V(4,3) = 4 + 12 + 24 + 24 = 64.
Pre počet všetkých jedno až štvorciferných čísel začínajúcich nulou bude zrejme platiť
V(3,1)+V(3,2)+V(3,3) = 1 + 3 + 6 + 6 =16.
Pre počet všetkých jedno až štvorciferných čísel z cifier 0, 1, 2, 3 je rovný
64 - 16
Koľko rôznych jedno až štvorciferných čísel môžeme vytvoriť z cifier 0, 1, 2, 3?
Riešenie
Keby medzi ciframi nebola nula, tak počet všetkých jedno až štvorciferných čísel by bol súčet čísel
V(4,1)+V(4,2)+V(4,3)+V(4,3) = 4 + 12 + 24 + 24 = 64.
Pre počet všetkých jedno až štvorciferných čísel začínajúcich nulou bude zrejme platiť
V(3,1)+V(3,2)+V(3,3) = 1 + 3 + 6 + 6 =16.
Pre počet všetkých jedno až štvorciferných čísel z cifier 0, 1, 2, 3 je rovný
64 - 16
Úloha 3.
K vyhotoveniu vlajky, ktorá má byť zložená z troch rôznofarebných vodorovných pruhov, sú k dispozícii látky farby modrej, červenej, zelenej, bielej a žltej.
K vyhotoveniu vlajky, ktorá má byť zložená z troch rôznofarebných vodorovných pruhov, sú k dispozícii látky farby modrej, červenej, zelenej, bielej a žltej.
- Určte počet vlajok, ktoré možno z látok týchto 5 farieb zostaviť.
- Koľko ich má v strede modrý pruh?
- Koľko ich má (kdekoľvek) biely pruh?
- Koľko ich nemá uprostred červený pruh?
Vytváranie farebnej zostavy/vlajky pomocou appletu. Zvoľte farbu a priraďte ju niektorému štvorčeku mriežky.
Cvičenie. Vytvorte všetky zostavy, ktoré sú zložené z 3 štvorčekov siete. Použite len 2 farby - modrú a žltú.
Variácie s opakovaním
Z prvkov množiny  je možné vytvoriť skupiny po
je možné vytvoriť skupiny po  prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny
prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny  . Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
. Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
 je možné vytvoriť skupiny po
je možné vytvoriť skupiny po  prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny
prvkov najvoľnejšie tak, že na každé miesto v tejto skupine umiestnime ľubovoľný prvok množiny  . Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
. Takto vzniknutým skupinám budeme hovoriť variácie s opakovaním. V závere predchádzajúcej kapitoly sme v rámci cvičenia vytvárali takéto skupiny - farebné zostavy. Farby sa mohli opakovať a zároveň záležalo na poradí.
Definícia.
Usporiadaná -tica prvkov množiny
-tica prvkov množiny 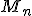 sa nazýva
sa nazýva  -variácia s opakovaním množiny
-variácia s opakovaním množiny 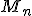 .
Počet všetkých
.
Počet všetkých  -variácií s opakovaním množiny
-variácií s opakovaním množiny 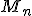 budeme označovať symbolom
budeme označovať symbolom 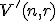 .
.
Usporiadaná
 -tica prvkov množiny
-tica prvkov množiny 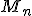 sa nazýva
sa nazýva  -variácia s opakovaním množiny
-variácia s opakovaním množiny 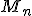 .
Počet všetkých
.
Počet všetkých  -variácií s opakovaním množiny
-variácií s opakovaním množiny 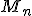 budeme označovať symbolom
budeme označovať symbolom 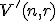 .
.
Príklad.
Utvorte všetky 3-variácie s opakovaním množiny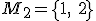 .
.
Riešenie.
Postupne vytvárajme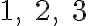 -variácie s opakovaním množiny
-variácie s opakovaním množiny 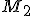 .
.
Utvorte všetky 3-variácie s opakovaním množiny
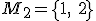 .
.
Riešenie.
Postupne vytvárajme
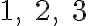 -variácie s opakovaním množiny
-variácie s opakovaním množiny 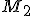 .
.
Veta.
Pre počet všetkých -variácií s opakovaním množiny
-variácií s opakovaním množiny 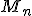 platí vzťah
platí vzťah 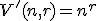
Dôkaz.
Použitím matematickej indukcie. Pre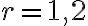 je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre
je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre  . Teda
. Teda
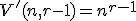
Všetky usporiadané -tice s opakovaním množiny
-tice s opakovaním množiny 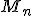 možno vytvoriť z
možno vytvoriť z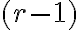 -tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny
-tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny 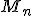 . Preto z každej
. Preto z každej 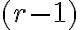 -tice získame
-tice získame  rôznych
rôznych  -tíc. Využitím indukčného predpokladu dostaneme
-tíc. Využitím indukčného predpokladu dostaneme
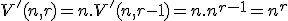 .
.
Pre počet všetkých
 -variácií s opakovaním množiny
-variácií s opakovaním množiny 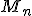 platí vzťah
platí vzťah 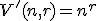
Dôkaz.
Použitím matematickej indukcie. Pre
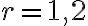 je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre
je tvrdenie pravdivé, presvedčte sa o tom. Predpokladajme, že tvrdenie platí pre  . Teda
. Teda
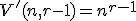
Všetky usporiadané
 -tice s opakovaním množiny
-tice s opakovaním množiny 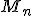 možno vytvoriť z
možno vytvoriť z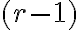 -tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny
-tíc tak, že ku každej dodáme na koniec po jednom každý prvok
množiny 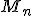 . Preto z každej
. Preto z každej 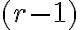 -tice získame
-tice získame  rôznych
rôznych  -tíc. Využitím indukčného predpokladu dostaneme
-tíc. Využitím indukčného predpokladu dostaneme
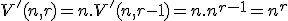 .
.
Urobte dôkaz využitím kombinačného pravidla súčinu.
Permutácie s opakovaním
Definícia.
Permutácie s opakovaním z prvkov je usporiadaná
prvkov je usporiadaná  -tica zostavená z týchto prvkov tak, že každý sa v nej vyskytuje aspoň raz.
-tica zostavená z týchto prvkov tak, že každý sa v nej vyskytuje aspoň raz.
Permutácie s opakovaním z
 prvkov je usporiadaná
prvkov je usporiadaná  -tica zostavená z týchto prvkov tak, že každý sa v nej vyskytuje aspoň raz.
-tica zostavená z týchto prvkov tak, že každý sa v nej vyskytuje aspoň raz.
Vzťah medzi  a
a  je nasledujúci:
je nasledujúci:
Prirodzené číslo udáva počet rôznych prvkov.
Jednotlivé prvky sa môžu opakovať. Je zvykom označovať
udáva počet rôznych prvkov.
Jednotlivé prvky sa môžu opakovať. Je zvykom označovať
 označuje počet všetkých prvkov, ktorých rôzne poradie skúmame, preto platí
označuje počet všetkých prvkov, ktorých rôzne poradie skúmame, preto platí 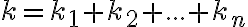 .
.
 a
a  je nasledujúci:
je nasledujúci:
Prirodzené číslo
 udáva počet rôznych prvkov.
Jednotlivé prvky sa môžu opakovať. Je zvykom označovať
udáva počet rôznych prvkov.
Jednotlivé prvky sa môžu opakovať. Je zvykom označovať
 označuje počet všetkých prvkov, ktorých rôzne poradie skúmame, preto platí
označuje počet všetkých prvkov, ktorých rôzne poradie skúmame, preto platí 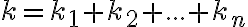 .
.
Príklad.
Tri modré kocky a 2 červené kocky ukladáme do radu. Zrejme záleží na poradí, pričom modrá kocka sa opakuje 4.krát a červená kocka sa opakuje 2-krát. Jedná sa o permutácie s opakovaním z dvoch prvkov/kategórií, kde prvý prvok sa opakuje 3x, druhý 2x.
Tri modré kocky a 2 červené kocky ukladáme do radu. Zrejme záleží na poradí, pričom modrá kocka sa opakuje 4.krát a červená kocka sa opakuje 2-krát. Jedná sa o permutácie s opakovaním z dvoch prvkov/kategórií, kde prvý prvok sa opakuje 3x, druhý 2x.
Dostaneme 15 rôznych uložení 3 modrých a dvoch červených kociek.
Tvrdenie.
Počet permutácií s opakovaním z , v ktorých sa jednotlivé prvky opakujú
, v ktorých sa jednotlivé prvky opakujú 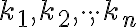 -krát, je rovný číslu
-krát, je rovný číslu
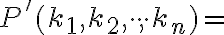
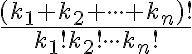
Počet permutácií s opakovaním z
 , v ktorých sa jednotlivé prvky opakujú
, v ktorých sa jednotlivé prvky opakujú 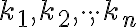 -krát, je rovný číslu
-krát, je rovný číslu
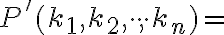
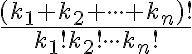
Dôkaz.
Podobne ako v predchádzajúcom príklade určíme, koľkými spôsobmi by bolo možné prvky/štvorčeky zoradiť. Celkom je prvkov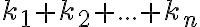 , počet všetkých ich zoradení (permutácií) je preto
, počet všetkých ich zoradení (permutácií) je preto
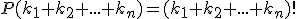 .
.
Pretože prvky nie sú všetky navzájom rôzne, budú sa niektoré v poradí opakovať:
Prvý prvok sa bude opakovať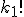 .
.
...
Pre každý prvok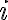 -tý je počet opakovaní rovný
-tý je počet opakovaní rovný 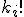 . Výsledný počet poradí všetkých pasteliek je preto
. Výsledný počet poradí všetkých pasteliek je preto
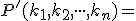
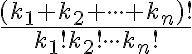
Podobne ako v predchádzajúcom príklade určíme, koľkými spôsobmi by bolo možné prvky/štvorčeky zoradiť. Celkom je prvkov
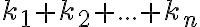 , počet všetkých ich zoradení (permutácií) je preto
, počet všetkých ich zoradení (permutácií) je preto 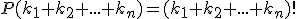 .
.Pretože prvky nie sú všetky navzájom rôzne, budú sa niektoré v poradí opakovať:
Prvý prvok sa bude opakovať
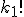 .
.
...
Pre každý prvok
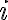 -tý je počet opakovaní rovný
-tý je počet opakovaní rovný 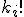 . Výsledný počet poradí všetkých pasteliek je preto
. Výsledný počet poradí všetkých pasteliek je preto
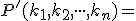
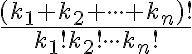
Partície
Teória partícií predstavuje jednu z najpozoruhodnejších častí klasickej kombinatoriky. V tomto odseku ukážeme len niekoľko zaujímavých výsledkov.
Obyčajne sa pri štúdiu partícií rozlišujú dva prípady. Partície, v ktorých
 pozostávajúcich z presne
pozostávajúcich z presne  sčítancov
sčítancov 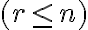 symbolom
symbolom
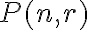 .
.
V ďalšom sa budeme snažiť určiť číslo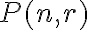 .
.
- záleží na poradí sčítancov
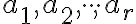 , napríklad partície
, napríklad partície
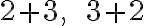 čísla
čísla 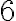 budeme považovať za rôzne
budeme považovať za rôzne
- nezáleží na poradí sčítancov
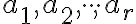 , napríklad partície
, napríklad partície
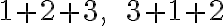 budeme považovať totožné
budeme považovať totožné
 pozostávajúcich z presne
pozostávajúcich z presne  sčítancov
sčítancov 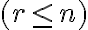 symbolom
symbolom
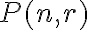 .
.
V ďalšom sa budeme snažiť určiť číslo
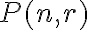 .
.
Nakreslime na priamke vedľa seba  bodov. Medzi nimi máme
bodov. Medzi nimi máme 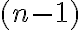 medzier a zvoľme z nich
medzier a zvoľme z nich 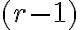 medzier. Táto voľba sa dá zrejme uskutočniť
medzier. Táto voľba sa dá zrejme uskutočniť
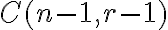
spôsobmi. Vložme do nich zvislé čiarky. Napr.: Rozdeliť číslo 6 na 4 časti znamená zvoliť 3 medzery z 5.

Tým sa pôvodných bodov rozdelí na
bodov rozdelí na  častí, pričom rôznym voľbám
častí, pričom rôznym voľbám 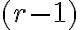 medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla
medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla 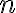 na
na
 častí. Dokázali sme vlastne vetu o počte partícií.
častí. Dokázali sme vlastne vetu o počte partícií.
 bodov. Medzi nimi máme
bodov. Medzi nimi máme 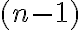 medzier a zvoľme z nich
medzier a zvoľme z nich 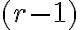 medzier. Táto voľba sa dá zrejme uskutočniť
medzier. Táto voľba sa dá zrejme uskutočniť
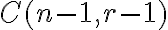
spôsobmi. Vložme do nich zvislé čiarky. Napr.: Rozdeliť číslo 6 na 4 časti znamená zvoliť 3 medzery z 5.

Tým sa pôvodných
 bodov rozdelí na
bodov rozdelí na  častí, pričom rôznym voľbám
častí, pričom rôznym voľbám 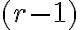 medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla
medzier zodpovedajú rôzne rozdelenia (aspoň čo do poradia ), čiže partícií čísla 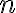 na
na
 častí. Dokázali sme vlastne vetu o počte partícií.
častí. Dokázali sme vlastne vetu o počte partícií.
Príklad. Rozklad čísla 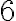 na
na 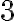 nenulových sčítancov. Vypíšte všetky rozklady.
nenulových sčítancov. Vypíšte všetky rozklady.
Riešenie. Číslo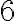 má
má
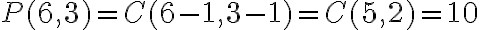 partícií z troch sčítancov. Sú to partície:
partícií z troch sčítancov. Sú to partície:
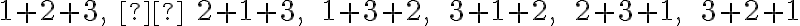
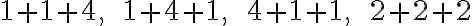 . Otvorte si applet Tu
. Otvorte si applet Tu
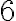 na
na 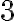 nenulových sčítancov. Vypíšte všetky rozklady.
nenulových sčítancov. Vypíšte všetky rozklady.
Riešenie. Číslo
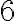 má
má
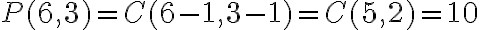 partícií z troch sčítancov. Sú to partície:
partícií z troch sčítancov. Sú to partície:
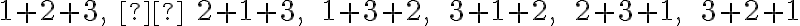
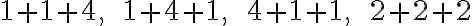 . Otvorte si applet Tu
. Otvorte si applet Tu
Teraz už ľahko určíme počet všetkých rôznych (aspoň) poradím partícií čísla 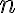 . Ak si to číslo označíme symbolom
. Ak si to číslo označíme symbolom
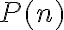 , tak zrejme platí
, tak zrejme platí
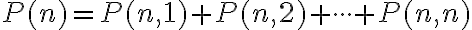 .
.
Použitím vety a identity
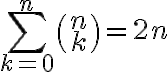
potom dostávame
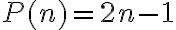 .
.
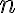 . Ak si to číslo označíme symbolom
. Ak si to číslo označíme symbolom
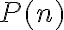 , tak zrejme platí
, tak zrejme platí
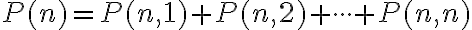 .
.
Použitím vety a identity
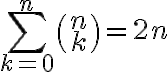
potom dostávame
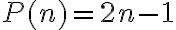 .
.
Partície úzko súvisia s kombináciami s opakovaním. Pokúsme sa vyriešiť nasledujúcu úlohu - nakupovanie v obchode, ktorá predstavuje kombinácie s opakovaním.
Úloha. Koľkými spôsobmi môžeme urobiť nákup, ktorý pozostáva zo 5 litrov mlieka, ak v obchode majú tri druhy mlieka -nízkotučné, polotučné a plnotučné. V nákupe musia byť zastúpené všetky druhy mlieka. Podmienka: nákup musí obsahovať z každého druhu aspoň jeden liter mlieka. Vypíšte všetky možnosti nákupu.
Návod.
Návod.
- Označme si nákup ako usporiadanú trojicu prirodzených čísel
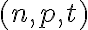 , kde jednotlivé čísla predstavujú koľko litrov sme nakúpili z daného druhu mlieka.
, kde jednotlivé čísla predstavujú koľko litrov sme nakúpili z daného druhu mlieka. - Napríklad trojica
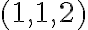 predstavuje nákup 1 litra nízkotučného mlieka a 1 litre polotučného a 2 litre plnotučného mlieka, preto nespĺňa podmienku nákupu.
predstavuje nákup 1 litra nízkotučného mlieka a 1 litre polotučného a 2 litre plnotučného mlieka, preto nespĺňa podmienku nákupu. - Trojica
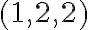 predstavuje nákup 1 litra nízkotučného mlieka a 2 litre polotučného a 2 litre plnotučného mlieka, preto spĺňa podmienku nákupu.
predstavuje nákup 1 litra nízkotučného mlieka a 2 litre polotučného a 2 litre plnotučného mlieka, preto spĺňa podmienku nákupu. - Trojica
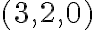 nepredstavuje nákup, keďže neobsahuje plnotučné mlieko.
nepredstavuje nákup, keďže neobsahuje plnotučné mlieko. - Nákup zrejme predstavuje partície - rozklad čísla 5 na tri nenulové sčítance. Vymenovaním všetkých partícií zistíme, že ich je práve 6.
- Vypíšte všetky 6 partície. Otvorte tabuľu Tu.
Tieto podmienky spĺňa zadanie našej úlohy. Sú to teda partície z 5 prvkov a 3 triedy. Pre počet všetkých platí
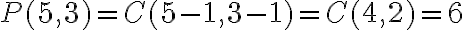 .
.Kombinácie s opakovaním
Nech
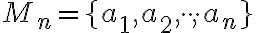 je množina
je množina  kategórií (druhov, prvkov). Vytvorme
kategórií (druhov, prvkov). Vytvorme  -tice z týchto
-tice z týchto
 prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad
prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad 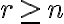 .
.
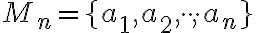 je množina
je množina  kategórií (druhov, prvkov). Vytvorme
kategórií (druhov, prvkov). Vytvorme  -tice z týchto
-tice z týchto
 prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad
prvkov, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Zrejme môže nastať aj prípad 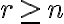 .
.
Definícia.
 -kombinácie s opakovaním definujeme ako
-kombinácie s opakovaním definujeme ako  -tice prvkov z
-tice prvkov z  druhov
druhov 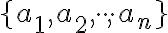 , v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých
, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých  -kombinácií s opakovaním z
-kombinácií s opakovaním z  prvkov budeme označovať symbolom
prvkov budeme označovať symbolom
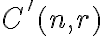 .
.
 -kombinácie s opakovaním definujeme ako
-kombinácie s opakovaním definujeme ako  -tice prvkov z
-tice prvkov z  druhov
druhov 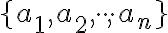 , v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých
, v ktorých nezáleží na poradí ale prvky (druhy) sa môžu opakovať. Počet všetkých  -kombinácií s opakovaním z
-kombinácií s opakovaním z  prvkov budeme označovať symbolom
prvkov budeme označovať symbolom
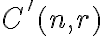 .
.
Príklad.
V obchode predávajú tri druhy cukru: kryštálový , práškový
, práškový  a hnedý
a hnedý 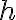 v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.
v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.
Riešenie. Uvedieme nejaké možné nákupy, napríklad 2 kilogramový nákup môže byť {1 kg práškového cukru, 1 kg kryštálového cukru}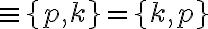 alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru}
alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru}
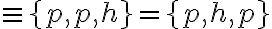 .
.
Všetky nákupy dvoch kilogramov budú predstavovať 2-kombinácie s opakovaním z troch druhov cukru -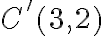 . Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru -
. Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru - 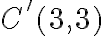 .
.
Pokúste sa vymenovať všetky možné nákupy. Pri nákupe
V obchode predávajú tri druhy cukru: kryštálový
 , práškový
, práškový  a hnedý
a hnedý 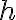 v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.
v kilogramovom balení. Vypíšte všetky možnosti pri nákupe 2 resp. 3 kilogramov cukru. V nákupe sa môže opakovať ten istý druh cukru.Riešenie. Uvedieme nejaké možné nákupy, napríklad 2 kilogramový nákup môže byť {1 kg práškového cukru, 1 kg kryštálového cukru}
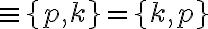 alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru}
alebo 3 kilogramový nákup môže byť {2 kg práškového cukru, 1 kg hnedého cukru}
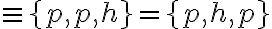 .
.Všetky nákupy dvoch kilogramov budú predstavovať 2-kombinácie s opakovaním z troch druhov cukru -
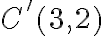 . Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru -
. Všetky nákupy troch kilogramov budú predstavovať 3-kombinácie s opakovaním z troch druhov cukru - 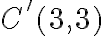 .
.
Pokúste sa vymenovať všetky možné nákupy. Pri nákupe
Dôkaz.
Nech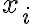 označuje počet výskytu prvku
označuje počet výskytu prvku
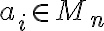 v nejakej
v nejakej  -kombinácií
-kombinácií 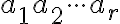 s opakovaním. Potom zrejme musí platiť rovnosť
s opakovaním. Potom zrejme musí platiť rovnosť
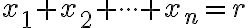 .
.
Napríklad pre nákup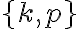 ide o rovnosť
ide o rovnosť 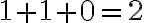
Nech
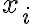 označuje počet výskytu prvku
označuje počet výskytu prvku
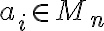 v nejakej
v nejakej  -kombinácií
-kombinácií 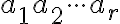 s opakovaním. Potom zrejme musí platiť rovnosť
s opakovaním. Potom zrejme musí platiť rovnosť
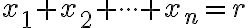 .
.
Napríklad pre nákup
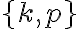 ide o rovnosť
ide o rovnosť 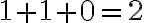
-
Ak k obidvom stranám tejto rovnosti pripočítame číslo
 , tak po menšej úprave dostaneme rovnosť
, tak po menšej úprave dostaneme rovnosť -
Na rovnosť
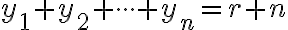 sa môžeme pozerať ako na rozdelenie čísla
sa môžeme pozerať ako na rozdelenie čísla 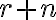 na
na  častí alebo ako na partície (navzájom rôznych aspoň poradím) čísla
častí alebo ako na partície (navzájom rôznych aspoň poradím) čísla 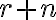 na
na  častí.
častí.
- Počet takýchto partícií je rovný číslu
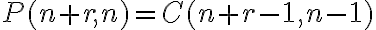 .Tým sme dokázali tvrdenie.
.Tým sme dokázali tvrdenie.
Pre nákup dvoch litrov dostávame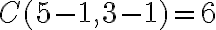 .
.
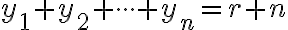 ,
,
kde
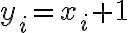 pre
pre 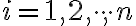 .
.
Pre nákup
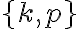 ide o rovnosť
ide o rovnosť 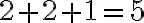 .
.
Na úlohy (pozrite tiež predchádzajúci príklad) typu:
"V obchode majú tri druhy sirupu: jahodový, malinový a pomarančový. Určite počet všetkých možností nákupu piatich fliaš sirupu v obchode."
sa môžeme pozerať aj ako na permutácie s opakovaním. Úlohu vyriešime tak, že určíme počet spôsobov, ako rozmiestniť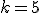 fliaš sirupu do
fliaš sirupu do 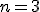 druhov/košov.
druhov/košov.
Použijeme dva symboly: • - fľaša; ↑-oddeľovač. Potom rozmiestnenia budú predstavovať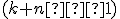 -tice, v ktorých sa symbol "•" vyskytuje
-tice, v ktorých sa symbol "•" vyskytuje 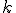 -krát (fľaše)
a symbol "↑"
-krát (fľaše)
a symbol "↑" 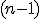 -krát (\\small ( n-1 \) oddelení medzi
-krát (\\small ( n-1 \) oddelení medzi 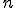 košmi).
košmi).

Rozmiestnenie symbolov predstavuje 2 jahodové sirupy, 0 malinový a 3 pomarančové sirupy alebo (122).
Počet takých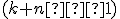 -tíc zodpovedá počtu permutácií zo 7 prvkov s opakovaním, kde sa prvý prvok opakuje/vyskytuje
-tíc zodpovedá počtu permutácií zo 7 prvkov s opakovaním, kde sa prvý prvok opakuje/vyskytuje 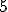 -krát a druhý
-krát a druhý 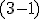 -krát. Tým sme ukázali platnosť vzťahu
-krát. Tým sme ukázali platnosť vzťahu
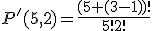 =
=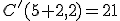 .
.
"V obchode majú tri druhy sirupu: jahodový, malinový a pomarančový. Určite počet všetkých možností nákupu piatich fliaš sirupu v obchode."
sa môžeme pozerať aj ako na permutácie s opakovaním. Úlohu vyriešime tak, že určíme počet spôsobov, ako rozmiestniť
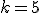 fliaš sirupu do
fliaš sirupu do 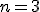 druhov/košov.
druhov/košov.
Použijeme dva symboly: • - fľaša; ↑-oddeľovač. Potom rozmiestnenia budú predstavovať
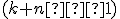 -tice, v ktorých sa symbol "•" vyskytuje
-tice, v ktorých sa symbol "•" vyskytuje 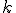 -krát (fľaše)
a symbol "↑"
-krát (fľaše)
a symbol "↑" 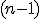 -krát (\\small ( n-1 \) oddelení medzi
-krát (\\small ( n-1 \) oddelení medzi 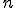 košmi).
košmi).
Rozmiestnenie symbolov predstavuje 2 jahodové sirupy, 0 malinový a 3 pomarančové sirupy alebo (122).
Počet takých
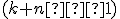 -tíc zodpovedá počtu permutácií zo 7 prvkov s opakovaním, kde sa prvý prvok opakuje/vyskytuje
-tíc zodpovedá počtu permutácií zo 7 prvkov s opakovaním, kde sa prvý prvok opakuje/vyskytuje 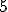 -krát a druhý
-krát a druhý 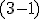 -krát. Tým sme ukázali platnosť vzťahu
-krát. Tým sme ukázali platnosť vzťahu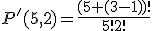 =
=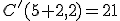 .
.Príklady/Cvičenie
- Vyžitím binomickej vety vypočítajte
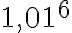 .
. - Určte desiaty člen binomického rozvoja výrazu
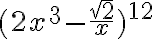
- "V obchode majú dva druhy kompótu: ananásový a hruškový. Určte počet všetkých možností nákupu 5 balení kompótu v tomto obchode." Otvorte tabuľu Tu.
Zistite, či riešením nasledujúcej úlohy dostaneme rovnaký výsledok?
"V obchode majú 5 druhov múky v kilogramovom balení: hladkú, polohrubú, hrubú, špeciálnu hladkú a bezlepkovú. Určte počet všetkých možností nákupu 2 kg múky v tomto obchode." Otvorte tabuľu Tu. - Kombinačné čísla
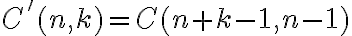 môžeme ľahko určiť z tabuľky
môžeme ľahko určiť z tabuľky
Otvorte tabuľku Tu
- Určte počet všetkých trojuholníkov, z ktorých žiadne dva nie sú zhodné a každá ich strana má jednu z veľkostí daných číslami 5, 6, 7, 8, 9, 10. [Rieš = 53: Zrejme pre trojice 448,449,459 neexistuje trojuholník - trojuholníková nerovnosť; máme 6 druhov strán a vytvárame trojice].
Princíp zapojenia a vypojenia
Príklad.
Písomnú prácu z matematiky písalo 35 študentov. Písomka obsahovala tri úlohy A, B, C. Vieme, že
Typické stredoškolské riešenie využíva grafickú schému - Vennov diagram, pomocou ktorého sa graficky vyjadruje príslušnosť prvkov k množine. V našom prípade to bude Vennov diagram pre tri množiny.
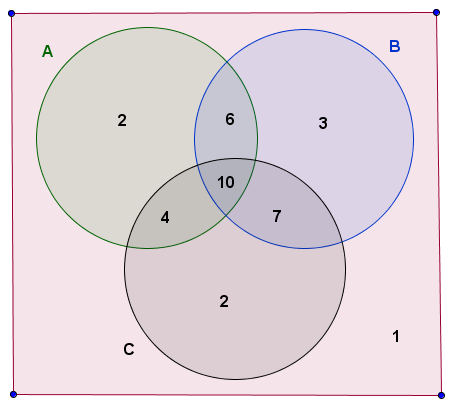
V diagrame postupne zapisujeme hodnoty
Písomnú prácu z matematiky písalo 35 študentov. Písomka obsahovala tri úlohy A, B, C. Vieme, že
- Úlohu A vyriešilo 22 študentov, úlohu B vyriešilo 26 študentov, úlohu C vyriešilo 23 študentov.
- Úlohu A aj úlohu B vyriešilo 16 študentov, úlohu A aj úlohu C vyriešilo 14 študentov, úlohu B aj úlohu C vyriešilo 17 študentov.
- Všetky úlohy vyriešilo 10 študentov. Zistite koľko študentov nevyriešilo ani jednu úlohu?
Typické stredoškolské riešenie využíva grafickú schému - Vennov diagram, pomocou ktorého sa graficky vyjadruje príslušnosť prvkov k množine. V našom prípade to bude Vennov diagram pre tri množiny.

V diagrame postupne zapisujeme hodnoty
Základný vzťah
V tejto časti budeme používať symboliku z predchádzajúcej kapitoly. Napríklad 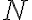 označuje počet všetkých objektov skúmanej množiny.
označuje počet všetkých objektov skúmanej množiny.
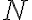 označuje počet všetkých objektov skúmanej množiny.
označuje počet všetkých objektov skúmanej množiny.
Tvrdenie
V kombinatorike princíp zapojenia a vypojenia alebo princíp exklúzie a inklúzie hovorí, že ak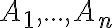 sú konečné množiny, tak
sú konečné množiny, tak
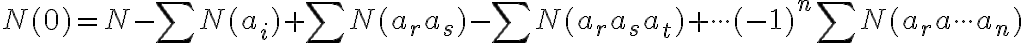
V kombinatorike princíp zapojenia a vypojenia alebo princíp exklúzie a inklúzie hovorí, že ak
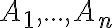 sú konečné množiny, tak
sú konečné množiny, tak
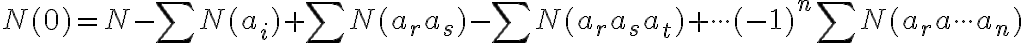
Dôkaz tvrdenia.
- Objekt, ktorý nemá ani jednu z vlastností
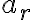 prispieva jednotkou k číslu
prispieva jednotkou k číslu 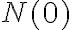 aj k číslu
aj k číslu 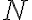 , ale vo zvyšných sčítancoch na pravej strane sa nevyskytuje.
, ale vo zvyšných sčítancoch na pravej strane sa nevyskytuje. - Ak nejaký objekt má
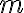 vlastností, kde
vlastností, kde 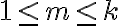 , potom prispieva
, potom prispieva - jednotkou k číslu N
-
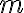 jednotkami k sume
jednotkami k sume 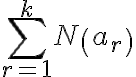 (lebo prispieva jednotkou k
(lebo prispieva jednotkou k 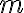 sčítancom)
sčítancom) 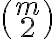 jednotkami k sume
jednotkami k sume 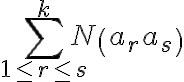 . (Z
. (Z 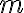 vlastností daného objektu možno vybrať
vlastností daného objektu možno vybrať 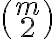 dvojíc, preto objekt prispieva k tejto sume
dvojíc, preto objekt prispieva k tejto sume 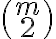 jednotkami), atď.
jednotkami), atď.- Teda objekt s
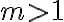 vlastnosťami prispieva k pravej strane rovnosti hodnotou
vlastnosťami prispieva k pravej strane rovnosti hodnotou
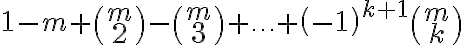
- Podľa binomickej vety vieme, že táto hodnota (striedavé sčítanie a odčítanie kombinačných čísel
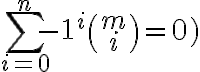 je rovná nule.
je rovná nule. - Preto celkový príspevok objektu s aspoň jednou vlastnosťou k obidvom stranám rovnosti je rovný nule.
Problém šatniarky
Problém šatniarky.
Pri vstupe do klubu si každý z piatich pánov odloží klobúk do šatne. Pri odchode šatniarka vydá náhodne každému pánovi jeden klobúk bez toho, že by skontrolovala, či je to správny klobúk. Aké sú šance, že žiaden z pánov nedostane vlastný klobúk?
Pri vstupe do klubu si každý z piatich pánov odloží klobúk do šatne. Pri odchode šatniarka vydá náhodne každému pánovi jeden klobúk bez toho, že by skontrolovala, či je to správny klobúk. Aké sú šance, že žiaden z pánov nedostane vlastný klobúk?
- Pravdepodobnosť bude predstavovať podiel počtu permutácií bez pevného bodu k počtu všetkých permutácií.
- Ide o permutácie klobúkov. Šatniarka priraďuje klobúky pánom.
- Jedno priradenie klobúkov pánom je permutácia. Predstavme si, že páni sú očíslovaní a klobúky tiež.
- Keď permutácia má pevný bod, tak to znamená, že niektorý klobúk bol daný správne svojmu pánovi.
- Čitateľ bude rovný počtu všetkých permutácií
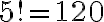 mínus počet permutácií s aspoň jedným pevným bodom - to musíme spočítať.
mínus počet permutácií s aspoň jedným pevným bodom - to musíme spočítať. - Na permutácie s aspoň jedným pevným bodom sa uplatňuje princíp inklúzie a exklúzie.
Aplikovaním princípu zapojenia a vypojenia (tvrdenie v predchádzajúcej kapitole) dostaneme: