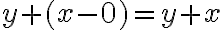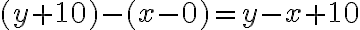Didaktika matematiky

Slovné úlohy na priamu a nepriamu úmernosť podporujú rozvoj funkčného myslenia žiakov. Ich zaradenie považuje didaktika matematiky za prvoradé a zároveň aj prioritné. Pri ich riešení sa využíva štandardný model pre úmernosť - trojčlenka. Uvedieme dve typické úlohy spolu s ich riešením.

Úloha.
Priemerná spotreba automobilu je 6 litrov benzínu na 100 kilometrov, akú vzdialenosť vie automobil pri tejto spotrebe prejsť na plnú nádrž, ktorá má 40 litrov?
Riešenie.

1. Zvislosť medzi spotrebou benzínu a prejdenou vzdialenosťou je priama závislosť. Teda, čím viac kilometrov prejde automobil, tým väčšia je spotreba pohonných hmôt. ;
2. Zapíšme prvý riadok trojčlenky: 6 litrov ............................100 km
3. Zapíšme druhý riadok trojčlenky: 40 litrov ............................ x km
4. Trojčlenku podčiarkneme. Vedľa trojčlenky nakreslíme šípky tým istým smerom. Potom celý zápis riešenia by mohol vyzerať nasledovne:

Nepriama úmernosť je závislosť dvoch veličín, pre ktoré platí:

• koľkokrát sa zväčší prvá veličina, toľkokrát sa zmenší druhá veličina alebo
• koľkokrát sa zmenší prvá veličina, toľkokrát sa zväčší druhá veličina.

Úloha.
Šiestim koňom vydrží zásoba sena 15 dní. Ako dlho vydrží táto zásoba sena 9 koňom?
Riešenie.

1. Zvislosť medzi spotrebou sena a počtom dní je nepriama závislosť. Teda, čím viac koní sa bude kŕmiť pri rovnakej zásobe krmiva, tým menší počet dní im krmivo vystačí.
2. Zapíšme prvý riadok trojčlenky: 6 koní ............................ 15 dní
3. Zapíšme druhý riadok trojčlenky: 9 koní ............................ x dní
4. Trojčlenku podčiarkneme. Vedľa trojčlenky nakreslíme šípky opačnými smermi. Potom celý zápis riešenia by mohol vyzerať nasledovne:

Niekedy pri riešní slovných úloh je vhodné kombinovať rôzne vizualizácie. Najčastejšie sa kombinuje tabuľkový model s rovnicovým modelom. Uvedieme upravenú úlohu a jej riešenie od autora Mgr. Vladimíra Kobzu, PhD., Katedra matematiky FPV UMB Banská Bystrica.

Úloha.
Keď bude mať Katka toľko rokov, koľko má dnes Janko, bude Janko o 10 rokov starší ako je Katka dnes. Koľko rokov mal Janko v čase, keď sa Katka narodila?
Riešenie.

1. Pri riešení tejto slonej úlohy slovnú úlohu je vhodné zaviesť tabuľku pre osoby (Janko a Katka) a pre 3 chronologické časové hladiny (vtedy, dnes, potom).
   Do tabuľky pomocou písmen/neznámych vpíšeme údaje zo zadania slovnej úlohy. Pritom sa snežíme vhodne zapísať vzťahy medzi týmito neznámymi. Zadane našej úlohy nám umožňuje zapísať údaje, ktoré majú otvorený ale aj skrytý výskyt.
2. Otvorený výskyt (údaje priamo uvedené v zadaní):
   • Stav „vtedy“ uvažuje situáciu, keď sa Katka narodila, teda:
     • Katkin vek pri narodení bol ... 0 rokov
     • Jankov vek pri jej narodení ... $x$ rokov
   • Stav dnes:
     • Katkin vek je ... $y$ rokov
   • Stav „potom“ popisuje vetná konštrukcia „Janko o 10 rokov starší ako je Katka dnes". Napríklad Janko bude o 10 rokov starší ako je Katka dnes predstavuje rovnicu ( y + 10 \) rokov

4. Skrytý výskyt (údaje, ktoré je možné odvodiť z kontextu zadania):
   • rozdiel vekov medzi Jankom a Katkou je konštantný a v priebehu časových hladín „vtedy“, „dnes“ a „potom“ sa nemení:
     • Janko dnes ... $y + (x - 0) = y + x$
     • Katka potom ... $(y + 10)-(x-0) = y-x + 10$
   
5. Hľadané údaje
   • úlohou je určiť hodnotu neznámej x (transformácia vetnej konštrukcie v otázke „koľko rokov mal Janko v čase, keď sa Katka narodila“, ide o vyjadrenie situácie v časovej hladine „vtedy“).
     
6. Analýzou situácie „keď bude mať Katka toľko rokov, koľko má dnes Janko“ získavame ďalšie vzťahy:
$y + x = y - x + 10$,
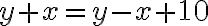čo je rovnica o dvoch neznámych ale jej riešenie pre x je číslo 5. Riešenie pre neznámu y je ľubovoľné nezáporné celé číslo (má nekonečne veľa riešení).
7. Na základe tohto môžeme vysloviť slovnú odpoveď pre našu slovnú úlohu:  Katka sa narodila v čase, keď mal Janko 5 rokov.