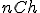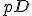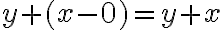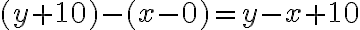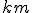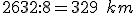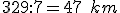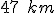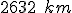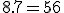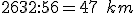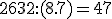Slovné úlohy
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Slovné úlohy |
| Vytlačil(a): | Gast |
| Dátum: | streda, 3 júla 2024, 13:42 |
Vymedzenie pojmov
Problematika riešenia slovných úloh tvorí dôležitú časť didaktiky matematiky.
Riešenie slovných úloh sa vyznačuje pomerne veľkou náročnosťou tak pre riešiteľov/žiakov ale aj pre učiteľa pri výklade metodiky riešenia týchto úloh.
V práci (Hejný, 2003) sa uvádza, že " ... hlavnou prekážkou úspešného riešenia slovných úloh je neschopnosť žiaka porozumieť úlohe, pochopiť situáciu opísanú úlohou a/alebo výzvu, ktorú úloha kladie".
Pojem slovná úloha v literatúre, ktorá sa venuje didaktike matematiky nie je plne ustálený. Uvedieme definíciu z práce (Šedivý, 2013).
V práci (Hejný, 2003) sa uvádza, že " ... hlavnou prekážkou úspešného riešenia slovných úloh je neschopnosť žiaka porozumieť úlohe, pochopiť situáciu opísanú úlohou a/alebo výzvu, ktorú úloha kladie".
Pojem slovná úloha v literatúre, ktorá sa venuje didaktike matematiky nie je plne ustálený. Uvedieme definíciu z práce (Šedivý, 2013).
Definícia.
Úlohy, v ktorých je závislosť medzi danými a hľadanými údajmi vyjadrená slovnou formuláciou a teba v nich riešiť istý problém zo spoločenskej, ekonomickej alebo inej životnej oblasti, nazývame slovné úlohy. Slovná úloha si vyžaduje jazykové porozumenie a presah do životnej skúsenosti.
Úlohy, v ktorých je závislosť medzi danými a hľadanými údajmi vyjadrená slovnou formuláciou a teba v nich riešiť istý problém zo spoločenskej, ekonomickej alebo inej životnej oblasti, nazývame slovné úlohy. Slovná úloha si vyžaduje jazykové porozumenie a presah do životnej skúsenosti.
Poznámky.
V práci (Hejný, 2003) sa pri zavedení pojmu slovná úloha uvádzajú aj ďalšie charakteristiky
V práci (Hejný, 2003) sa pri zavedení pojmu slovná úloha uvádzajú aj ďalšie charakteristiky
- termínom slovná úloha sa rozumie matematická úloha, ktorá si vyžaduje jazykové porozumenie
- slovnú úlohu nazveme dynamickou alebo príbehom, ak sa jej príbeh odohráva vo viacerých časových hladinách.
- úlohu, v ktorej čas nehrá dôležitú rolu, nazveme statickou alebo situáciou.
W. Blum a M. Niss (1991 uvádzajú tieto dôvody pre zaradenie slovných úloh do vyučovania matematiky
- sú vhodným prostriedkom na rozvíjanie všeobecných kompetencií žiakov a postojov k matematike
- umožňujú žiakom porozumieť použitiu matematiky
- rozvíjajú schopnosť žiakov aktivovať matematické vedomosti v mimo matematických situáciách.
Cvičenie
Ktorým z nasledujúcich štyroch úloh môžete prisúdiť prívlastok „slovná“. Zdôvodnite svoje rozhodnutia.
- Učiteľ napísal na tabuľu rovnicu
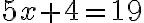 . Potom sa opýtal triedy, či by niekto vedel rovnicu vyriešiť. Vy by ste vedeli?
. Potom sa opýtal triedy, či by niekto vedel rovnicu vyriešiť. Vy by ste vedeli? - Súčet dvoch čísel je 19 a rozdiel je 3. Ktoré sú to čísla?
- Sestry Klára a Lenka majú dovedna 19 rokov. Klára má o 3 roky viac ako Lenka. Koľko rokov má Klára a koľko Lenka?
- Sestry Klára a Lenka majú dovedna 19 rokov. Klára mala 3 roky, keď sa Lenka narodila. Koľko rokov má Klára a koľko Lenka?
Príklad zdôvodnenia:
Všetkých 6 úloh je formulovaných pomocou slov a sú teda „slovné“. Ale podľa nami uvedenej definície prvú úlohu nemôžeme nazvať slovnou, lebo k jej vyriešeniu slovám netreba rozumieť. Jej riešenie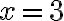 nájde i človek ktorý po slovensky nevie. Táto úloha nevyžaduje jazykové porozumenie.
nájde i človek ktorý po slovensky nevie. Táto úloha nevyžaduje jazykové porozumenie.
Všetkých 6 úloh je formulovaných pomocou slov a sú teda „slovné“. Ale podľa nami uvedenej definície prvú úlohu nemôžeme nazvať slovnou, lebo k jej vyriešeniu slovám netreba rozumieť. Jej riešenie
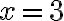 nájde i človek ktorý po slovensky nevie. Táto úloha nevyžaduje jazykové porozumenie.
nájde i človek ktorý po slovensky nevie. Táto úloha nevyžaduje jazykové porozumenie.
Cvičenie.
Vypracuje rešerš práce Hejný, M.: Anatómia slovnej úlohy o veku. Práca je publikovaná v zborníku z konferencie 11th Slovak-Czech-Polish Mathematical School.
Vypracuje rešerš práce Hejný, M.: Anatómia slovnej úlohy o veku. Práca je publikovaná v zborníku z konferencie 11th Slovak-Czech-Polish Mathematical School.
Matematizácia slovnej úlohy
Štruktúra slovnej úlohy je tvorená z troch základných častí:
- podrobný popis situácie, v ktorej sa príbeh odohráva
- číselné údaje potrebné k úspešnému vyriešeniu úlohy, tieto časti nazývame podmienky úlohy
- otázka, ktorá opisuje to, čo máme vypočítať. Vyriešiť slovnú úlohu znamená previesť príbeh či situáciu do formalizovaného jazyka (najčastejšie do rovnice či sústavy rovníc). Takto vznikne matematický model úlohy.
Poznámka.
Podľa profesora Šedivého žiadnu slovnú úlohu nemôžeme vyriešiť dovtedy, kým nebola jasne sformulovaná ako príslušná matematická úloha.
Sformulovanie vhodnej a správnej matematickej úlohy sa pri riešení slovnej úlohy považuje za najdôležitejšiu časť riešenia slovnej úlohy. Túto skutočnosť by mal mať na zreteli aj učiteľ pri hodnotení.
Podľa profesora Šedivého žiadnu slovnú úlohu nemôžeme vyriešiť dovtedy, kým nebola jasne sformulovaná ako príslušná matematická úloha.
Sformulovanie vhodnej a správnej matematickej úlohy sa pri riešení slovnej úlohy považuje za najdôležitejšiu časť riešenia slovnej úlohy. Túto skutočnosť by mal mať na zreteli aj učiteľ pri hodnotení.
V práci (Šedivý, 2013) sa uvádza: "Prechod od slovnej úlohy k matematickej úlohe sa nazýva matematizácia slovnej úlohy. Spätný prechod od výsledku matematickej úlohy k výsledku slovnej úlohy sa nazýva interpretácia výsledkov matematickej úlohy v pôvodnej situácii."
Schému riešenia slovnej úlohy môžeme znázorniť takto:
Slovná úloha → Rozbor → Matematická úloha (MÚ) → Riešenie MÚ → Výsledok + Odpoveď
Pri riešení slovnej úlohy významnú úlohu zohráva vizualizácia slovnej úlohy. Vizualizácia predstavuje grafické znázornenie situácie, v ktorej sa príbeh odohráva. Žiak pri znázorňovaní danej situácie vytvára grafický prepis informácií zo zadania slovnej úlohy do určitého diagramu (modelu, obrázku), ktorý mu pomáha popisovať vzťahy medzi objektmi príbehu.
Grafický model úlohy je niekedy súčasťou procesu riešenia. Budeme to interpretovať na možných riešeniach nasledujúcej úlohy.
Úloha.
Sestry Klára a Lenka majú dovedna 19 rokov. Klára mala 3 roky, keď sa Lenka narodila. Koľko rokov má Klára a koľko Lenka?
Sestry Klára a Lenka majú dovedna 19 rokov. Klára mala 3 roky, keď sa Lenka narodila. Koľko rokov má Klára a koľko Lenka?
Možné riešenia.
-
Žiaci na nižšom stupni vzdelávania často používajú pri riešení takýchto úloh metódu pokus - omyl: napríklad použijú "bodkový" model
Klára ••••• •••••
a potom o tri bodky menej k Lenke
Lenka ••••• ••
Spočítajú bodky v obidvoch radoch a zistia, že výsledok 17 je málo. Pridajú ešte po jednej bodke do každého riadku a úlohu majú vyriešenú. -
Starší žiaci už využijú "rovnicový model", ktorý je považovaný za štandardný. Rovnicový model úlohy bude mať tvar:
 ,
,
kde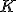 = počet rokov Kláry a
= počet rokov Kláry a 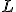 = počet rokov Lenky.
= počet rokov Lenky.
Vizualizácia - modely
Na vizualizáciu slovnej úlohy sa využívajú rôzne diagramy, ktoré žiakom umožňujú ľahšie porozumenie vzájomných vzťahov medzi objektmi zo skúmaného príbehu. Uvedieme niektoré modely vizualizácie, ktoré sa pomerne často používajú na 2. stupni základnej školy.
- rovnicový alebo tiež algebraický model
- tabuľkový model
- úsečkový model
- množinový model
Použitie týchto modelov budeme interpretovať pri riešení nasledujúcej úlohy.
Úloha.
V triede je 25 žiakov, z ktorých je 12 chlapcov. Pán učiteľ na hodine telesnej výchovy zistil, že 5 chlapcov vie plávať a 2 dievčatá nevedia plávať. Koľko žiakov vie a koľko nevie plávať? (in Šedivý a kol. 2013)
V triede je 25 žiakov, z ktorých je 12 chlapcov. Pán učiteľ na hodine telesnej výchovy zistil, že 5 chlapcov vie plávať a 2 dievčatá nevedia plávať. Koľko žiakov vie a koľko nevie plávať? (in Šedivý a kol. 2013)
- Rovnicový model je vhodný pre vyššie ročníky resp. pre nadanejších žiakov. Tento model ja charakteristický tým, že pre hľadané číselné údaje zavedieme označenie pomocou symbolov (najčastejšie ako písmená - neznáme).
a) základné údaje: spolu ... 25 žiakov; chlapcov ... 12; dievčat ... 25 - 12 = 13
b) plavci: chlapci... 5
dievčatá ...
c) neplavci: chlapci...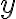
dievčatá ... 2
d) odpovedajúce rovnice: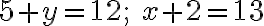
- Tabuľkový model umožňuje prehľadne modelovať údaje a vzťahy medzi nimi
- Úsečkový model - viac o využití takýchto modelov nájdete v práci Novotná (2004). Tiež pozri (Hofmanová, 2019,str. 7).
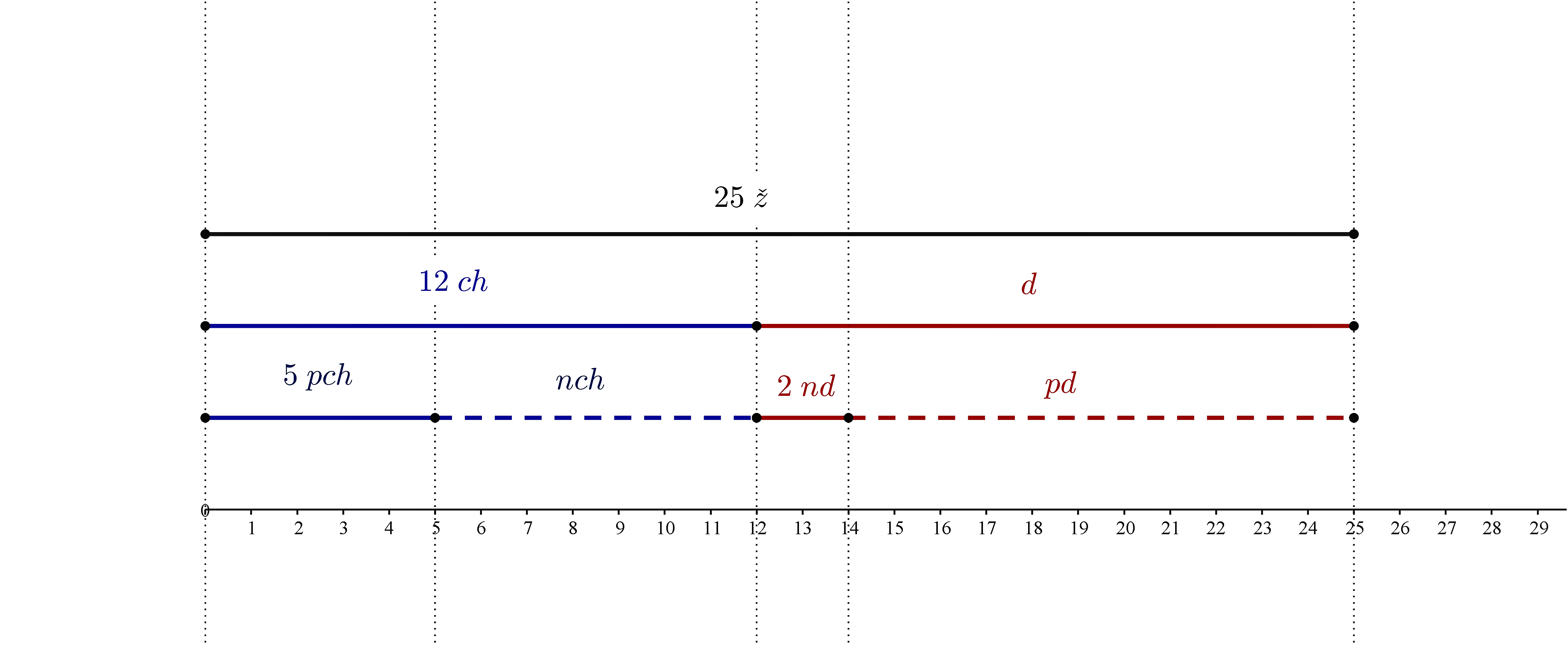
- Množinový model spočíva vo využívaní Vennových diagramov pri riešení slovných úloh. Pri riešení úlohy o schopnosti žiakov plávať použijeme Vennov diagram pre dve disjunktné množiny.Pri riešení využívame vlastnosť o počte prvkov (kardinálnom čísle) zjednotenia dvoch množín
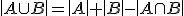 ,
,
ktorej platnosť je zrejmá z Vennovho diagramu pre dve množiny.
Ak použijeme množinový diagram pre disjunktné množiny
a postupným dopĺňaním číselných údajov do upraveného Vennovho diagramu dostaneme pre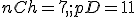 .
.
Špecifické modely
Slovné úlohy na priamu a nepriamu úmernosť podporujú rozvoj funkčného myslenia žiakov. Ich zaradenie považuje didaktika matematiky za prvoradé a zároveň aj prioritné. Pri ich riešení sa využíva štandardný model pre úmernosť - trojčlenka. Uvedieme dve typické úlohy spolu s ich riešením.
Úloha.
Priemerná spotreba automobilu je 6 litrov benzínu na 100 kilometrov, akú vzdialenosť vie automobil pri tejto spotrebe prejsť na plnú nádrž, ktorá má 40 litrov?
Riešenie.
Priemerná spotreba automobilu je 6 litrov benzínu na 100 kilometrov, akú vzdialenosť vie automobil pri tejto spotrebe prejsť na plnú nádrž, ktorá má 40 litrov?
Riešenie.
- Zvislosť medzi spotrebou benzínu a prejdenou vzdialenosťou je priama závislosť. Teda, čím viac kilometrov prejde automobil, tým väčšia je spotreba pohonných hmôt. ;
- Zapíšme prvý riadok trojčlenky: 6 litrov ............................100 km
- Zapíšme druhý riadok trojčlenky: 40 litrov ............................ x km
- Trojčlenku podčiarkneme. Vedľa trojčlenky nakreslíme šípky tým istým smerom. Potom celý zápis riešenia by mohol vyzerať nasledovne:
Nepriama úmernosť je závislosť dvoch veličín, pre ktoré platí:
- koľkokrát sa zväčší prvá veličina, toľkokrát sa zmenší druhá veličina alebo
- koľkokrát sa zmenší prvá veličina, toľkokrát sa zväčší druhá veličina.
Úloha.
Šiestim koňom vydrží zásoba sena 15 dní. Ako dlho vydrží táto zásoba sena 9 koňom?
Riešenie.
Šiestim koňom vydrží zásoba sena 15 dní. Ako dlho vydrží táto zásoba sena 9 koňom?
Riešenie.
- Zvislosť medzi spotrebou sena a počtom dní je nepriama závislosť. Teda, čím viac koní sa bude kŕmiť pri rovnakej zásobe krmiva, tým menší počet dní im krmivo vystačí.
- Zapíšme prvý riadok trojčlenky: 6 koní ............................ 15 dní
- Zapíšme druhý riadok trojčlenky: 9 koní ............................ x dní
- Trojčlenku podčiarkneme. Vedľa trojčlenky nakreslíme šípky opačnými smermi. Potom celý zápis riešenia by mohol vyzerať nasledovne:
Niekedy pri riešní slovných úloh je vhodné kombinovať rôzne vizualizácie. Najčastejšie sa kombinuje tabuľkový model s rovnicovým modelom. Uvedieme upravenú úlohu a jej riešenie od autora Mgr. Vladimíra Kobzu, PhD., Katedra matematiky FPV UMB Banská Bystrica.
Úloha.
Keď bude mať Katka toľko rokov, koľko má dnes Janko, bude Janko o 10 rokov starší ako je Katka dnes. Koľko rokov mal Janko v čase, keď sa Katka narodila?
Riešenie.
Keď bude mať Katka toľko rokov, koľko má dnes Janko, bude Janko o 10 rokov starší ako je Katka dnes. Koľko rokov mal Janko v čase, keď sa Katka narodila?
Riešenie.
- Pri riešení tejto slonej úlohy slovnú úlohu je vhodné zaviesť tabuľku pre osoby (Janko a Katka) a pre 3 chronologické časové hladiny (vtedy, dnes, potom).
Do tabuľky pomocou písmen/neznámych vpíšeme údaje zo zadania slovnej úlohy. Pritom sa snežíme vhodne zapísať vzťahy medzi týmito neznámymi. Zadane našej úlohy nám umožňuje zapísať údaje, ktoré majú otvorený ale aj skrytý výskyt. - Otvorený výskyt (údaje priamo uvedené v zadaní):
- Stav „vtedy“ uvažuje situáciu, keď sa Katka narodila, teda:
- Stav dnes:
- Stav „potom“ popisuje vetná konštrukcia „Janko o 10 rokov starší ako je Katka dnes". Napríklad Janko bude o 10 rokov starší ako je Katka dnes predstavuje rovnicu ( y + 10 \) rokov
- Skrytý výskyt (údaje, ktoré je možné odvodiť z kontextu zadania):
- rozdiel vekov medzi Jankom a Katkou je konštantný a v priebehu časových hladín „vtedy“, „dnes“ a „potom“ sa nemení:
- Hľadané údaje
- úlohou je určiť hodnotu neznámej x (transformácia vetnej konštrukcie v otázke „koľko rokov mal Janko v čase, keď sa Katka narodila“, ide o vyjadrenie situácie v časovej hladine „vtedy“).
- úlohou je určiť hodnotu neznámej x (transformácia vetnej konštrukcie v otázke „koľko rokov mal Janko v čase, keď sa Katka narodila“, ide o vyjadrenie situácie v časovej hladine „vtedy“).
- Analýzou situácie „keď bude mať Katka toľko rokov, koľko má dnes Janko“ získavame ďalšie vzťahy:
- Na základe tohto môžeme vysloviť slovnú odpoveď pre našu slovnú úlohu: Katka sa narodila v čase, keď mal Janko 5 rokov.
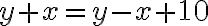 ,
,
čo je rovnica o dvoch neznámych ale jej riešenie pre x je číslo 5. Riešenie pre neznámu y je ľubovoľné nezáporné celé číslo (má nekonečne veľa riešení).
Klasifikácia slovných úloh
Slovné úlohy podľa počtu počtových operácií rozdeľujeme na:
- Jednoduché slovné úlohy sú také úlohy, pri ktorých riešenie si vyžaduje iba jednu počtovú operáciu.
- Zložené slovné úlohy - pri ich riešení je nutné použiť aspoň dve alebo viac počtových operácii.
Ukážky jednoduchých slovných úloh. Klasifikácia a triedenie je prevzaté z práce (Šedivý, 2013).
V jednoduchej slovnej úlohe je reálna situácia popísaná dvoma zadanými numeickými údajmi a úlohou je určiť neznámy číselný údaj. V nižších ročníkoch základnej školy riešime jednoduché slovné úlohy len v obore prirodzených čísel. Tieto ďalej kategorizujeme podľa druhu počtovej operácie, ktorá sa používa pri ich riešení. Sú to úlohy:
V jednoduchej slovnej úlohe je reálna situácia popísaná dvoma zadanými numeickými údajmi a úlohou je určiť neznámy číselný údaj. V nižších ročníkoch základnej školy riešime jednoduché slovné úlohy len v obore prirodzených čísel. Tieto ďalej kategorizujeme podľa druhu počtovej operácie, ktorá sa používa pri ich riešení. Sú to úlohy:
- Na sčítanie
- Máme určiť súčet, keď sú dané obidva sčítance. Napríklad:
V jedom košíku na stole je 5 jabĺk a v druhom košíku sú 4 jablká. Koľko jabĺk je spolu v obidvoch košíkoch na stole?
- Potrebujeme zväčšiť dané číslo a niekoľko jednotiek. Napríklad:
Janko má 15 rokov, Evka má o 7 rokov viac. Koľko rokov má Evka?
- Máme určiť súčet, keď sú dané obidva sčítance. Napríklad:
- Na odčítanie
- Určenie jedného sčítanca, ak je daný súčet a druhý sčítanec. Napríklad:
Katka má 19 kociek lega. Na vytvorenie domčeka použila 15 kociek. Koľko kociek jej zostalo?
- Zmenšenie daného čísla o niekoľko jednotiek. Napríklad:
Boris má 20 EUR. Igor má o 6 EUR menej. Koľko EUR má Igor?
- Porovnávanie rozdielom. Napríklad:
O koľko je číslo 48 väčšie ako číslo 16?
- Určenie jedného sčítanca, ak je daný súčet a druhý sčítanec. Napríklad:
- Na násobenie
- Určenie súčtu rovnakých sčítancov. Napríklad:
Anička si ušetrila každý deň 10 centov. Koľko centov si ušetrila za 7 dní?
- Zväčšenie čísla niekoľkokrát. Napríklad:
Chodník je široký 2m. Cesta je štyrikrát širšia. Aká široká je cesta?
- Určenie počtu všetkých usporiadaných dvojíc. Napríklad:
Na šachovom turnaji sa vytvorili dve skupiny. V skupine A boli: Janka Adam a Zuzka. V skupine B boli: Peter, Tomáš, Betka a Juraj.
Súťažili tak, že každý člen skupiny A hral s každým členom skupiny B. Koľko šachových partií sa počas turnaja odohralo?
- Určenie súčtu rovnakých sčítancov. Napríklad:
- Na delenie
- Delenie na rovnaké časti - daný je celok a počet časti. Treba určiť veľkosť jednej časti. Napríklad:
Vladko priniesol na ihrisko 35 cukríkov a chcel ich spravodlivo rozdeliť medzi svojich 7 kamarátov. Koľko cukríkov dostal každý z nich?
- Delenie podľa obsahu - je daný celok a veľkosť jednej časti. Treba určiť počet všetkých častí. Napríklad:
Koľkým kamarátom mohol Vladko rozdeliť 35 cukríkov, ak chcel dať každému ich po 7 cukríkov?
- Zmenšenie čísla niekoľkokrát. Napríklad:
V hodinárstve je 18 budíkov. Náramkových hodín je trikrát menej. Koľko náramkových hodín je v hodinárstve?
- Porovnanie podielom. Napríklad:
V knižnici je 120 nemeckých kníh a 40 anglických kníh. Koľkokrát viac je v knižnici nemeckých kníh?
- Delenie na rovnaké časti - daný je celok a počet časti. Treba určiť veľkosť jednej časti. Napríklad:
Osobitnú pozornosť pri nácviku riešenia slovných úloh si vyžadujú nepriame úlohy, ktorých formulácia zvádza k opačnej počtovej operácii. Napríklad:
Alenka má 30 sponiek, čo je o 13 menej ako má Zuzka. Koľko sponiek má Zuzka?
Andrej má 21 kartičiek hokejistov, čo je trikrát viac ako má kartičiek futbalistov. Koľko kartičiek futbalistov má Andrej?
Ľuboš mal na začiatku hry na ruke niekoľko kariet. Z kopy si potiahol ešte 5 kariet, čim mal na ruke 9 kariet. Koľko kariet mal Ľuboš na začiatku hry na ruke?
Alenka má 30 sponiek, čo je o 13 menej ako má Zuzka. Koľko sponiek má Zuzka?
Andrej má 21 kartičiek hokejistov, čo je trikrát viac ako má kartičiek futbalistov. Koľko kartičiek futbalistov má Andrej?
Ľuboš mal na začiatku hry na ruke niekoľko kariet. Z kopy si potiahol ešte 5 kariet, čim mal na ruke 9 kariet. Koľko kariet mal Ľuboš na začiatku hry na ruke?
Poznámky.
Slovné úlohy podľa typu počtových operácii, ktoré použijeme pri riešení matematickej úlohy rozdeľujeme:
- Aditívne slovné úlohy - pri ich riešení používame operácie sčítania a odčítania.
- Multiplikativne slovné úlohy - pri ich riešení používame operácie násobenia.
- Koľko spolu?“
- O koľko viac (menej)?“
Zložené slovné úlohy
Zloženú slovnú úlohu riešime tak, že ju postupne transformujeme na postupnosť nadväzujúcich jednoduchých úloh tak, aby výsledok poslednej jednoduchej úlohy bol výsledkom
pôvodnej zloženej úlohy. Táto transformácia sa najčastejšie realizuje dvoma spôsobmi, ktoré nazývame -
analytický a syntetický spôsob riešenia zloženej slovnej úlohy.
- Pri analytickom spôsobe riešenia zloženej slovnej úlohy sa snažíme formulovať postupnosť vhodných otázok. Finálna otázka smeruje k počtovej operácii a k číslu, ktoré nám dáva odpoveď na otázku v pôvodnej slovnej úlohe.
- Pri syntetickom spôsobe riešenia vychádzame z konkrétnych číselných údajov, ktoré sú dané v podmienke. Vyberieme z nich dve vhodné a sformulujeme jednoduchú úlohu. Postupne takýmto spôsobom formulujeme ďalšie jednoduché slovné úlohy. Pokračujeme tak dlho, dokiaľ neprídeme k odpovedi na danú otázku. Kombináciou obidvoch spôsobov dostávame analyticko-syntetický postup.
Riešenie zloženej slovnej úlohy má zvyčajne tri fázy
- Rozbor úlohy predstavuje oboznámenie sa s úlohou čítaním s porozumením, analýzou grafického diagramu, určením otázok a podmienok, termínov a vzťahov;
- Zostavenie plánu riešenia zahŕňa symbolické znázornenie, znázornenie diagramom a pod., určenie postupu riešenia - zostavenie rovnice, nerovnice, zápis počtových operácií;
- 3. Výpočet - uskutočnenie výpočtu, kontrola správnosti výpočtu a výsledkov, odpoveď.
Príklad.
Skupina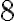 pretekárov prejde spolu za
pretekárov prejde spolu za 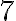 dní na bicykli
dní na bicykli 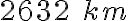 . Koľko
. Koľko 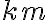 prejde jeden pretekár za jeden deň, ak predpokladáme rovnaký výkon u každého zúčastneného pretekára?
prejde jeden pretekár za jeden deň, ak predpokladáme rovnaký výkon u každého zúčastneného pretekára?
Skupina
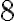 pretekárov prejde spolu za
pretekárov prejde spolu za 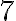 dní na bicykli
dní na bicykli 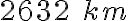 . Koľko
. Koľko 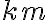 prejde jeden pretekár za jeden deň, ak predpokladáme rovnaký výkon u každého zúčastneného pretekára?
prejde jeden pretekár za jeden deň, ak predpokladáme rovnaký výkon u každého zúčastneného pretekára?
Riešenie
A. Analytické riešenie
A. Syntetické riešenie
A. Analytické riešenie
A. Syntetické riešenie
Typy slovných úloh
Slovné úlohy môžeme kategorizovať aj podľa
- matematického postupu, ktorý využijeme pri riešení alebo podľa
- ich obsahového zamerania.
Podľa matematického postupu, ktorý využijeme pri riešení delíme slovné úlohy na
- priamu úmernosť
- nepriamu úmernosť
Príklady.
- Usušením 3 kg čerstvých sliviek sme získali 750 g sušených sliviek. Koľko kilogramov čerstvých sliviek treba usušiť, ak chceme získať 1,5 kg sušených sliviek?
- Dva stroje vyrobia za 50 hodín 2000 výrobkov. Koľko strojov potrebujeme prikúpiť, aby sme za 30 hodín vyrobili 15000 výrobkov ?
Podľa obsahového zamerania delíme slovné úlohy na úlohy
- o rovnomernom pohybe
- o spoločnej práci
- na operácie so zlomkami a percentami
- kombinatorické, ... Ďalšie triedenie a ukážky riešení nájdete v práci (Hofmanová, 2019)
Príklady.
Poznámky.
- ...
- ...
Zoznam použitej literatúry
Literatúra
- Blum, W., Niss, M. Applied mathematical problem solving, modelling, applications, and links to other subjects — State, trends and issues in mathematics instruction. Educ Stud Math 22, 37–68 (1991). https://doi.org/10.1007/BF00302716.
- Hejný, M. (1995), Zmocňování se slovní úlohy. Pedagogika XLV, 1995, str. 386-399.
- Hejný, M. (2003). Anatómia slovnej úlohy o veku. Disputationes scientificae Universitatis Catholicae in Ružomberok, 3(3), 21–32. Dostupné Tu
- Hofmanová, A. (2019), Matematika - slovné úlohy & všetko ostatné. Vydavateľstvo Hofmanová. ISBN 9788089616497. Ukážka Tu.
- Kobza, V. (2014). Modelové riešenie problémovej úlohy. Dostupné Tu.
- Šedivý, O. a kol. (2013), Vybrané kapitoly z didaktiky matematiky. FPV UKF Nitra. ISBN 978-80-558-0438-5.
- Pavlovičová, G., Švecová, V., Záhorská, J. (2010). Metódy riešenia matematických úloh pre štúdium učiteľstva pre primárne vzdelávanie. Nitra : UKF, 2010. 100 s. ISBN 978-80-8094-776-7.