Zavedenie číselných oborov N, Z, Q
Celé čísla
Riešenie - 4. až 9. úloha
Riešenie.
- Pri grafickom riešení nerovnice je potrebné zostrojiť graf kvadratickej funkcie
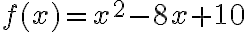 .
. - Najskôr určíme korene rovnice
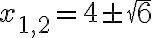 ,
,
pričom s výhodou môžeme pracovať v prostredí GeoGebra. Pozri stránku Kvadratická nerovnica v kurze Did_Mat, zvoľ príklad č.7.
- Potom určíme súradnice vrcholu
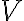 paraboly
paraboly
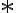 tak, že najskôr určíme hodnotu funkcie
tak, že najskôr určíme hodnotu funkcie
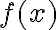 v bode
v bode
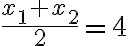
![(f(4)=-6) \Rightarrow (V=[4,-6] ) (f(4)=-6) \Rightarrow (V=[4,-6] )](https://lms.umb.sk/filter/tex/pix.php/d86e333ae6c9d06c9a0dd1d98beb126c.png) .
.
- Riešením nerovnice
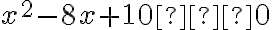 sú čísla
sú čísla
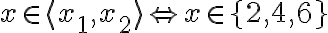
.
Riešenie.
- Hľadáme také dve čísla
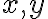 , pre ktoré platí
, pre ktoré platí
(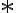 )
)
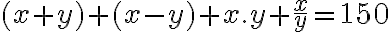 ,
,
pričom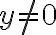 .
. - Prvé tri členy rovnice sú celé čísla, preto musí byť aj podiel
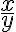
celé číslo , pre ktoré platí
, pre ktoré platí
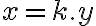 . Po dosadení do rovnice (
. Po dosadení do rovnice (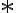 ) dostaneme
) dostaneme
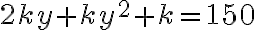 .
.
- Po úprave dostaneme rovnicu
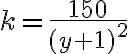 .
.
- Hľadáme druhé mocniny čísel, ktoré sú deliteľmi 150. Zrejme sú to len druhé mocniny čísel 1 a 5.
- Riešením rovnice
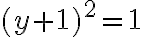 resp.
resp.
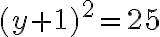
sú čísla
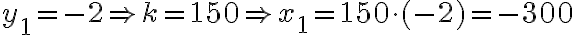
resp.
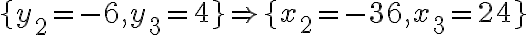 .
. - Hľadané dvojice čísel patria do množiny
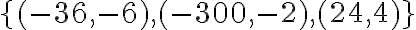
- Urobte skúšku správnosti.
Čísla
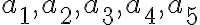 majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
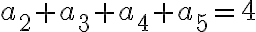 a zároveň
a zároveň
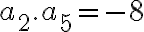 .
.
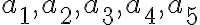 majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
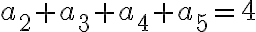 a zároveň
a zároveň
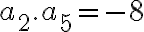 .
.
Riešenie.
-
Nech čísla
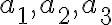 tvoria GeomPost s kvocientom
tvoria GeomPost s kvocientom
 a nech čísla
a nech čísla
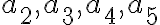 tvoria AritmPost s diferenciou
tvoria AritmPost s diferenciou
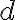 .
.
-
Zo zadania vyplýva, že
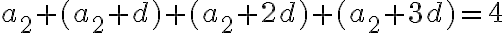 a zároveň
a zároveň
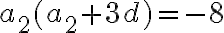 .
.
- To znamená vyriešiť sústavu dvoch rovníc o dvoch nezámych
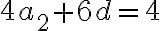
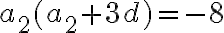 .
.
- Jej riešením sú celé čísla
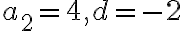 ,
,
odkiaľ dostaneme, že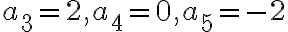 .
.
- Číslo
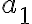 vypočítame tak, že najskôr určíme kvocient
vypočítame tak, že najskôr určíme kvocient
 ako podiel
ako podiel
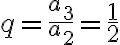
a potom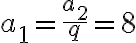 .
.
- Urobte skúšku správnosti.
Počet úchytov na záclone
-
Najjednoduchšie uchytenie záclon je také, pri ktorom máme nepretržite možnosť uchytiť záclonu v strede. Pozri obrázok.
- V prvom kroku použijeme tri úchyty – dva krajné a jeden v strede
- V ďalšom kroku by bolo výhodné, aby sme opäť mohli uchytiť stredy v ľavej aj v pravej časti záclony. To znamená mať dva úchyty pre tieto stredy. Spolu je to 5 úchytov.
- Nasleduje rekurentné vyjadrenie:
- ak máme uchytenú záclonu na
 miestach, tak v ďalšom kroku
miestach, tak v ďalšom kroku
- potrebujeme
 nových úchytov (pre všetky stredy)
nových úchytov (pre všetky stredy)
- spolu je to
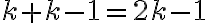 úchytov.
úchytov.
- Dostávame postupnosť, v ktorej
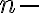 tý člen vyjadríme nasledovne. Začneme experimentovať pre „malé“ hodnoty. Po nie koľkých krokoch môžeme dôjsť k záveru, že pre n-tý člen platí rovnosť:
tý člen vyjadríme nasledovne. Začneme experimentovať pre „malé“ hodnoty. Po nie koľkých krokoch môžeme dôjsť k záveru, že pre n-tý člen platí rovnosť:
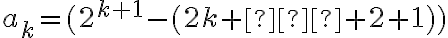 ,
,
ktorá predstavuje súčet dvoch hodnôt. - Prvá je rovná číslu
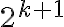 a druhá predstavuje súčet geometrickej postupnosti, kde prvý člen je rovný 1 a koeficient je rovný
a druhá predstavuje súčet geometrickej postupnosti, kde prvý člen je rovný 1 a koeficient je rovný
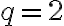 .
.
- Odkiaľ pre súčet dostaneme:
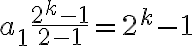 . Po dosadení získame explicitné vyjadrenie pre počet úchytov:
. Po dosadení získame explicitné vyjadrenie pre počet úchytov:

Pri určovaní počtu úchytiek použijeme nasledujúci algoritmus:
