Zavedenie číselných oborov N, Z, Q
Celé čísla
Riešenie - 1. až 3. úloha
U2: Dokážte, že pre ľubovoľné celé čísla
U3: Dokážte, že pre dve triedy 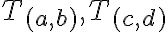 rozkladu
rozkladu
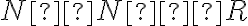 platí:
platí:
![[T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}] [T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/579a44e56178957e0450af29b0cff3be.png)
Ak dve triedy majú spoločný aspoň jeden prvok, tak sa rovnajú!
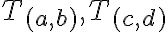 rozkladu
rozkladu
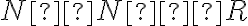 platí:
platí:
![[T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}] [T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/579a44e56178957e0450af29b0cff3be.png)
Ak dve triedy majú spoločný aspoň jeden prvok, tak sa rovnajú!
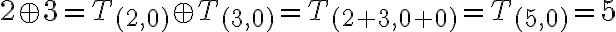
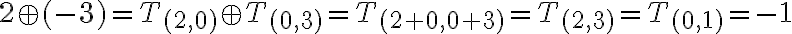
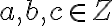
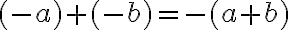
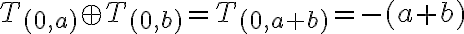
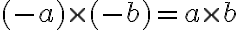
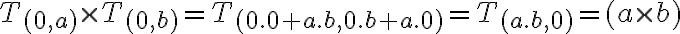
![(m,n) \in T_{(a,b)} \cap T_{(c,d)} \Leftrightarrow [(m,n) \in T_{(a,b)}] \wedge [(m,n) \in T_{(c,d)}] (m,n) \in T_{(a,b)} \cap T_{(c,d)} \Leftrightarrow [(m,n) \in T_{(a,b)}] \wedge [(m,n) \in T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/6b9bb6cec2ff04fcc24551a758137bd7.png)
![[a+m=n+b] \wedge [c+m=n+d] [a+m=n+b] \wedge [c+m=n+d]](https://lms.umb.sk/filter/tex/pix.php/951e9cedff5e1ece6baf75aba0af9439.png)
![[a-c=b-d] [a-c=b-d]](https://lms.umb.sk/filter/tex/pix.php/b4c3d57fae8a94dfc0e6c08d70568562.png)
![[a+d=b+c] [a+d=b+c]](https://lms.umb.sk/filter/tex/pix.php/7e0433909fe3be92805ff6e4f619f58a.png)
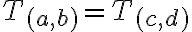
![[(m,n) \in T_{(a,b)}] \Leftrightarrow [T_{(m,n)}= T_{(a,b)}] [(m,n) \in T_{(a,b)}] \Leftrightarrow [T_{(m,n)}= T_{(a,b)}]](https://lms.umb.sk/filter/tex/pix.php/7b0c9bf5006d4d5499b2ae96ffe0e990.png)
