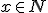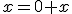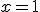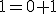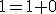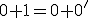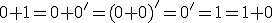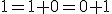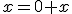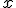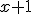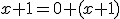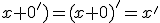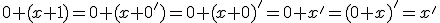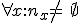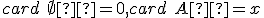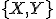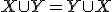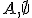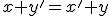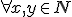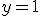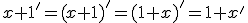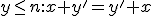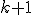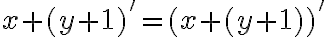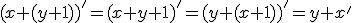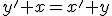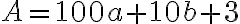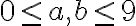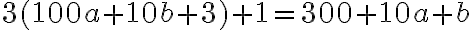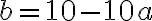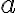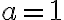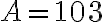Zavedenie číselných oborov N, Z, Q
Prirodzené čísla
Riešenia
A. V Peanovej aritmetike budeme dokazovať matematickou indukciou
B. V množinovej aritmetike budeme vychádzať z teórie množín
Budeme vychádzať z platnosti komutatívnosti sčítania pre prirodzené čísla: 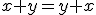 , pričom budeme dokazovať matematickou indukciou.
, pričom budeme dokazovať matematickou indukciou.
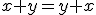 , pričom budeme dokazovať matematickou indukciou.
, pričom budeme dokazovať matematickou indukciou.
Trojciferné prirodzené číslo má na mieste jednotiek číslicu 3. Ak túto číslicu premiestnime na začiatok čísla, dostaneme nové číslo, ktoré je rovné trojnásobku pôvodného čísla zväčšeného o 1. Určte takéto trojciferné číslo.