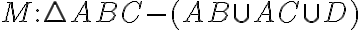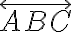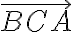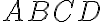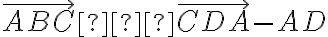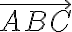Jordanova miera
Topologické pojmy
Základné topologické pojmy - definície (Spracované podľa práce [1])
Nech
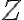 je základná množina, bod
je základná množina, bod
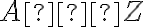 ,
, 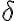 je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina
je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina 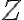 je pravidelný 7-uholník.
je pravidelný 7-uholník.
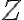 je základná množina, bod
je základná množina, bod
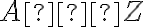 ,
, 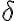 je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina
je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina 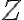 je pravidelný 7-uholník.
je pravidelný 7-uholník.
-
Okolie bodu
 (presnejšie
(presnejšie 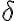 -okolie bodu
-okolie bodu
 ) je množina všetkých bodov
) je množina všetkých bodov
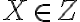 , pre ktoré platí, že úsečka
, pre ktoré platí, že úsečka
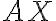 je menšia ako
je menšia ako 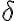 .
.
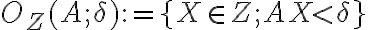
-
Nech
 je podmnožina množiny
je podmnožina množiny
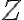 (
(
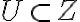 ).
Množina
).
Množina
 sa nazýva ohraničená množina, ak existuje taký bod v
sa nazýva ohraničená množina, ak existuje taký bod v
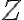 a také jeho
a také jeho 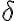 −okolie, pre ktoré platí, že
−okolie, pre ktoré platí, že
 je jeho podmnožinou.
V priloženom applete množina
je jeho podmnožinou.
V priloženom applete množina 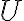 je nekonvexný 7-uholník.
je nekonvexný 7-uholník. - Nech
 je podmnožina množiny
je podmnožina množiny
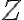 (
(
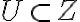 ).
Bod nazývame
).
Bod nazývame -
vnútorným bodom množiny
 , ak existuje také jeho
, ak existuje také jeho 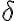 -okolie, ktoré je podmnožinou množiny
-okolie, ktoré je podmnožinou množiny
 .
. -
vonkajším bodom množiny
 , ak existuje také jeho
, ak existuje také jeho 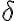 -okolie, ktorého prienik s množinou
-okolie, ktorého prienik s množinou
 je
prázdna množina.
je
prázdna množina. - hraničným bodom množiny
 , ak pre každé jeho
, ak pre každé jeho 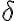 -okolie platí, že obsahuje aspoň jeden bod
množiny
-okolie platí, že obsahuje aspoň jeden bod
množiny
 a aspoň jeden bod, ktorý jej nepatrí.
a aspoň jeden bod, ktorý jej nepatrí. -
Hranica množiny
 je množinu všetkých jej hraničných bodov.
je množinu všetkých jej hraničných bodov. - Budeme hovoriť, že množina je
- uzavretá, ak každý jej hraničný bod jej patrí
- otvorená, ak aspoň jeden hraničný bod jej nepatrí.
- Dve množiny budeme nazývať neprekrývajúce sa, ak ich prienik neobsahuje žiaden vnútorný bod ani jednej z týchto množín.
Úlohy
_________________________________________________________________________________________
[1] Monoszová, G.: Planimetria - pomocný text ku prednáškam. Dostupné na: https://www.fpv.umb.sk/app/cmsFile.php?disposition=a&ID=20245