Euklidovský priestor
Metrické vzťahy
Kritérium kolmosti
Tvrdenie - kritérium kolmosti priamky a roviny.
Priamka je kolmá na rovinu práve vtedy, keď je kolmá na dve rôznobežné priamky tejto roviny.
Priamka je kolmá na rovinu práve vtedy, keď je kolmá na dve rôznobežné priamky tejto roviny.
Dôkaz
- Nutnosť (
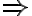 ). Predpokladajme, že
). Predpokladajme, že 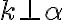 . Z kolmosti priamky
. Z kolmosti priamky  na všetky priamky roviny (definícia)
vyplýva jej kolmosť na ľubovoľné dve jej rôznobežky.
na všetky priamky roviny (definícia)
vyplýva jej kolmosť na ľubovoľné dve jej rôznobežky.
- Dostatočnosť
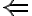 ). Nech priamka
). Nech priamka 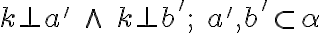 . Treba dokázať, že priamka k je kolmá na všetky priamky danej roviny.
Zvoľme si ľubovoľnú priamku
. Treba dokázať, že priamka k je kolmá na všetky priamky danej roviny.
Zvoľme si ľubovoľnú priamku 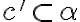 .
.
Podľa predchádzajúceho dôsledku je priamka s rovinou
s rovinou  rôznobežná.
Označme
rôznobežná.
Označme 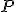 ich spoločný bod a zostrojme priamky
ich spoločný bod a zostrojme priamky 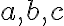 prechádzajúce týmto bodom a rovnobežné s priamkami
prechádzajúce týmto bodom a rovnobežné s priamkami 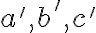 .
Stačí dokázať:
.
Stačí dokázať: 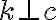 (prečo? vysvetlite).
(prečo? vysvetlite).
Otvorte si applet Tu
Zvoľme si ľubovoľné body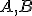 ležiace na rovnomenných priamkach tak, aby priamka
ležiace na rovnomenných priamkach tak, aby priamka 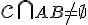 .
Označme
.
Označme 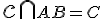 . Ďalej nech sú
. Ďalej nech sú 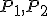 ľubovoľné dva body, pre ktoré je bod
ľubovoľné dva body, pre ktoré je bod 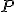 je stredom úsečky
je stredom úsečky 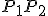 .
.
Potom platí: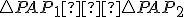 a
a 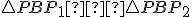 (sus)
(sus)
odkiaľ dostávame zhodnosť úsečiek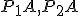 resp.
resp. 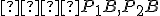 . Preto platí
. Preto platí
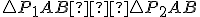 (sss)
(sss)
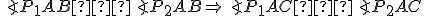 .
.
Dôsledkom je zhodnosť trojuholníkov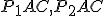 (sus), teda i zhodnosť úsečiek
(sus), teda i zhodnosť úsečiek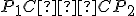 .
.
Preto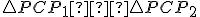 (sss), čo znamená, že sú zhodné i uhly v týchto trojuholníkoch pri vrchole
(sss), čo znamená, že sú zhodné i uhly v týchto trojuholníkoch pri vrchole  .
Pretože ide o susedné uhly, sú oba uhly pravé, t.j. priamka
.
Pretože ide o susedné uhly, sú oba uhly pravé, t.j. priamka  je kolmá na priamku
je kolmá na priamku  .
.
Poznámky.
- Kolmosť dvoch priamok je relácia symetrická ale nie je reflexívna ani tranzitívna.
- Kritérium kolmosti priamky a roviny vyjadruje nevyhnutnú a dostačujúcu podmienku kolmosti priamky a roviny, ale nehovorí nič o existencii takejto priamky. Existencia priamky kolmej na rovinu je dôsledkom nasledujúceho nasledujúcom tvrdenia.
- Namiesto vyjadrenia „priamka je kolmá na rovinu“ budeme tiež používať vyjadrenie „rovina je kolmá na priamku“. Analogicky ako v a) budeme hovoriť, že priamka a rovina sú navzájom kolmé.
Tvrdenie - existencia priamky kolmej na rovinu.
Existuje práve jedna priamka prechádzajúca daným bodom M a kolmá na danú rovinu α .
Existuje práve jedna priamka prechádzajúca daným bodom M a kolmá na danú rovinu α .
Dôkaz
- Existencia priamky kolmej na na priamku vyplýva z Euklidových tvrdení T/XI a T/XII zo Základov, Kniha 1. Existencia kolmice na rovinu sa dá zdôvodniť z týchto tvrdení a konštrukcie uvedenej v nasledujúcom applete.
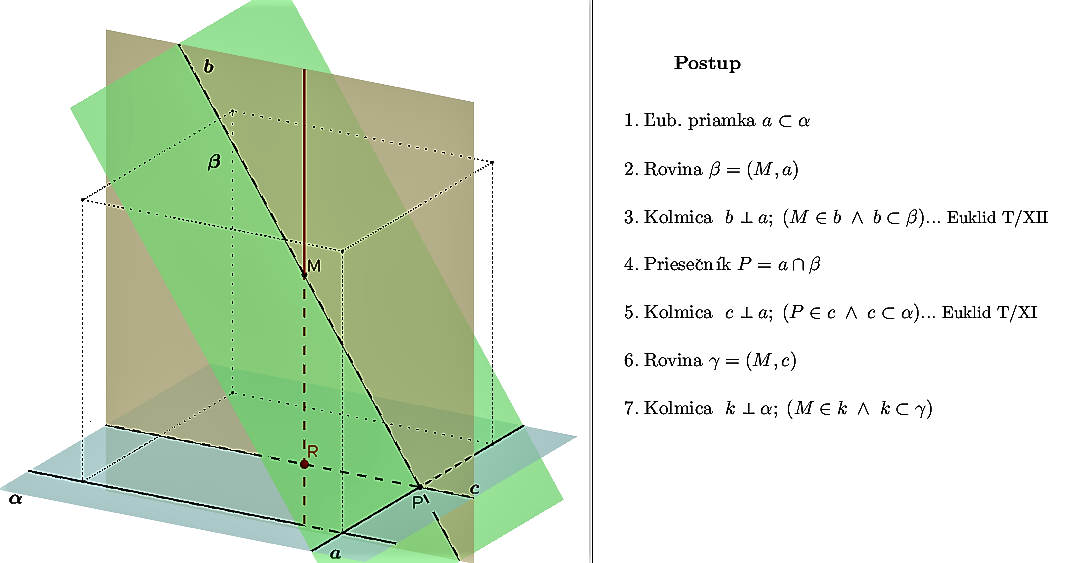 Applet Tu
Applet Tu - Jednoznačnosť takej kolmice dokážeme nepriamo s vyžitím obrázka
Ak by existovali dve navzájom rôzne priamky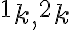 požadovanej vlastnosti, tak by ich priesečníky
požadovanej vlastnosti, tak by ich priesečníky 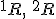 s rovinou
s rovinou  boli navzájom rôzne body a
trojuholník
boli navzájom rôzne body a
trojuholník 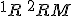 by bol trojuholníkom s dvoma pravými uhlami, čo je spor s vetou o súčte vnútorných uhlov v trojuholníku euklidovskej roviny.
by bol trojuholníkom s dvoma pravými uhlami, čo je spor s vetou o súčte vnútorných uhlov v trojuholníku euklidovskej roviny.
Tvrdenie - existencia roviny kolmej na priamku.
Existuje práve jedna rovina prechádzajúca daným bodom M a kolmá na danú priamku m.
Existuje práve jedna rovina prechádzajúca daným bodom M a kolmá na danú priamku m.
Dôkaz - analogický (konštrukčný) ako v predchádzajúcom tvrdení
Dôsledok
Dve roviny kolmé na tú istú priamku sú navzájom rovnobežné.
Dve roviny kolmé na tú istú priamku sú navzájom rovnobežné.
...
