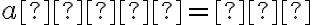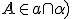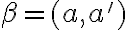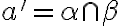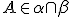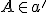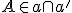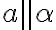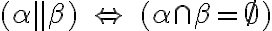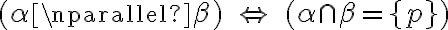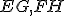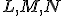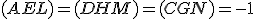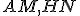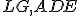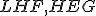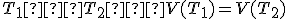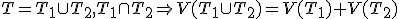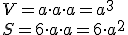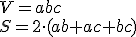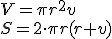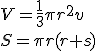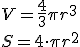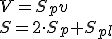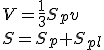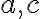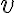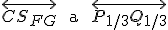Euklidovský priestor
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Euklidovský priestor |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:34 |
Historické poznámky
Trojrozmerný euklidovský priestor 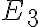 je systém troch množín
je systém troch množín 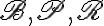 - bodov, priamok a rovín, ktoré spĺňajú axiómy incidencie, usporiadania, zhodnosti, rovnobežnosti a spojitosti.
- bodov, priamok a rovín, ktoré spĺňajú axiómy incidencie, usporiadania, zhodnosti, rovnobežnosti a spojitosti.
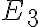 je systém troch množín
je systém troch množín 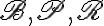 - bodov, priamok a rovín, ktoré spĺňajú axiómy incidencie, usporiadania, zhodnosti, rovnobežnosti a spojitosti.
- bodov, priamok a rovín, ktoré spĺňajú axiómy incidencie, usporiadania, zhodnosti, rovnobežnosti a spojitosti.
Stereometria sa zaoberá priestorovými problémami (stereometria, grécky stereos značí pevný, tuhý – metrein merať).
Platón skúmal pravidelné telesá, ktoré nazývame ešte aj dnes platónskymi telesami. Viac o Platónskych telesách nájdete Tu.

Euklides sa zapodieval stereometriou a poznal takmer všetky vety, ktoré sú v našej školskej stereometrii.
Platón skúmal pravidelné telesá, ktoré nazývame ešte aj dnes platónskymi telesami. Viac o Platónskych telesách nájdete Tu.

Euklides sa zapodieval stereometriou a poznal takmer všetky vety, ktoré sú v našej školskej stereometrii.
- Babylončania vedeli počítať objemy pevnostných násypov s lichobežníkovým prierezom.
- Egypt vyvinul určitý druh náuky na zisťovanie objemov sýpok, ktoré mali obyčajne tvar kvádra.
- Grécky filozof Demokritos (5. stor. pred n. l.) prvý zistil, že objem ihlana sa rovná jednej tretine objemu hranola.
- Povrch a objem gule vypočítal Archimedes (3 stor. pred n. l.).
Stereometria
Stereometria sa nazýva geometria založená na axiómach, základných definíciách a na vybudovanej planimetrii. Uvádzame len niektoré axiómy a definície.
Axiómy incidencie v rovine
I1: Dvoma rôznymi bodmi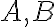 prechádza práve jedna priamka.
prechádza práve jedna priamka.
I2: Každá priamka obsahuje aspoň dva rôzne body.
I3: Existuje aspoň jedna trojica navzájom rôznych nekolineárnych bodov.
Axiómy incidencie v priestore
I4: Tromi nekolineárnymi bodmi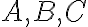 prechádza práve jedna rovina. Kocka Tu
prechádza práve jedna rovina. Kocka Tu
I5: V každej rovine existujú aspoň tri nekolineárne body.
I6: Ak dva rôzne body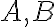 priamky
priamky  ležia v rovine
ležia v rovine  , potom každý bod priamky
, potom každý bod priamky  leží v rovine
leží v rovine  .
.
I7: Ak dve roviny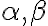 majú spoločný bod
majú spoločný bod
 , potom majú spoločný ešte aspoň jeden bod
, potom majú spoločný ešte aspoň jeden bod
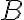 , rôzny od
, rôzny od
 .
.
I8: Existuje aspoň jedna štvorica nekomplanárnych bodov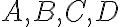 .
.
I1: Dvoma rôznymi bodmi
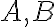 prechádza práve jedna priamka.
prechádza práve jedna priamka.
I2: Každá priamka obsahuje aspoň dva rôzne body.
I3: Existuje aspoň jedna trojica navzájom rôznych nekolineárnych bodov.
Axiómy incidencie v priestore
I4: Tromi nekolineárnymi bodmi
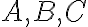 prechádza práve jedna rovina. Kocka Tu
prechádza práve jedna rovina. Kocka TuI5: V každej rovine existujú aspoň tri nekolineárne body.
I6: Ak dva rôzne body
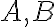 priamky
priamky  ležia v rovine
ležia v rovine  , potom každý bod priamky
, potom každý bod priamky  leží v rovine
leží v rovine  .
.
I7: Ak dve roviny
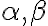 majú spoločný bod
majú spoločný bod
 , potom majú spoločný ešte aspoň jeden bod
, potom majú spoločný ešte aspoň jeden bod
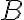 , rôzny od
, rôzny od
 .
.
I8: Existuje aspoň jedna štvorica nekomplanárnych bodov
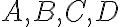 .
.
Definície
- vzájomná poloha dvoch priamok
- Dve priamky, ktoré ležia v jednej rovine a nemajú spoločný bod, sa nazývajú rovnobežné priamky alebo rovnobežky.
- Rôznobežky sú dve priamky, ktoré majú spoločný práve jeden bod. Spoločný bod sa nazýva priesečník priamok.
- Dve priamky, ktoré neležia v žiadnej rovine, sa nazývajú mimobežné priamky alebo mimobežky.
Poznámky.
- Množina bodov sa nazýva kolineárna, ak je incidentná s nejakou priamkou. Množina bodov sa nazýva komplanárna, ak je incidentná s nejakou rovinou.
- Ak každý bod priamky
 leží v danej rovine
leží v danej rovine  , hovoríme, že priamka
, hovoríme, že priamka  leží v rovine
leží v rovine  [je incidentná s rovinou
[je incidentná s rovinou  ];
hovoríme tiež, že rovina α prechádza priamkou
];
hovoríme tiež, že rovina α prechádza priamkou  .
. - Existencia mimobežných priamok je zaručená axiómou I8.
- Ak štvorica bodov
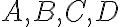 je nekomplanárna, tak dvojice priamok
je nekomplanárna, tak dvojice priamok
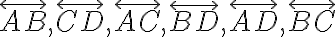 sú mimobežné. Ukážka Tu
sú mimobežné. Ukážka Tu
Doporučená literatúra
. - Sklenáriková, Z. – Čižmár, J.: Elementárna geometria euklidovskej roviny. Skriptum, vyd. UK, Bratislava 2002, ISBN 80-223-1585-0
- Klenková, P.: Stereometria – elementárna geometria trojrozmerného euklidovského priestoru, Diplomová práca, UK FMFI Bratislava 2006. Dostupné Tu
Rovnobežnosť útvarov
Definície - rovnobežnosť
- Priamky
 sú navzájom rovnobežné práve vtedy, ak
sú navzájom rovnobežné práve vtedy, ak 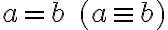 alebo existuje rovina, v ktorej obe priamky ležia a nemajú žiaden spoločný bod.
alebo existuje rovina, v ktorej obe priamky ležia a nemajú žiaden spoločný bod.
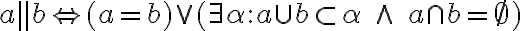
- Priamka
 je rovnobežná s rovinou
je rovnobežná s rovinou  práve vtedy, ak priamka
práve vtedy, ak priamka  leží v rovine α alebo s ňou nemá žiaden spoločný bod.
leží v rovine α alebo s ňou nemá žiaden spoločný bod.
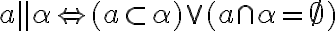
- Dve roviny
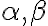 sú navzájom rovnobežné práve vtedy, ak: alebo α = β alebo tieto roviny nemajú žiaden spoločný bod.
sú navzájom rovnobežné práve vtedy, ak: alebo α = β alebo tieto roviny nemajú žiaden spoločný bod.
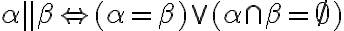
Poznámky
- Dve priamky sú rovnobežné, alebo rôznobežné, alebo mimobežné.
- Priamka je s rovinou rovnobežná, alebo rôznobežná.
- Dve roviny sú rovnobežné, alebo rôznobežné.
Kritérium rovnobežnosti priamky a roviny
Priamka je rovnobežná s rovinou
je rovnobežná s rovinou  práve vtedy, ak je rovnobežná s aspoň jednou priamkou
práve vtedy, ak je rovnobežná s aspoň jednou priamkou 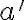 roviny
roviny  (
(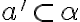 ). Symbolicky
). Symbolicky
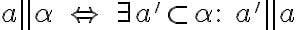 .
.
Priamka
 je rovnobežná s rovinou
je rovnobežná s rovinou  práve vtedy, ak je rovnobežná s aspoň jednou priamkou
práve vtedy, ak je rovnobežná s aspoň jednou priamkou 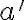 roviny
roviny  (
(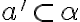 ). Symbolicky
). Symbolicky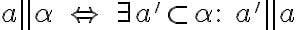 .
.
Dôkaz
- pri dokazovaní využijeme dichotomický princíp vzhľadom na prienik priamky  a roviny
a roviny 
 a roviny
a roviny 
- Nutná podmienka (dôkaz implikácie):
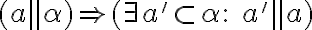 . V zmysle definície rovnobežnosti priamky a roviny, môžu nastať dva prípady:
. V zmysle definície rovnobežnosti priamky a roviny, môžu nastať dva prípady:
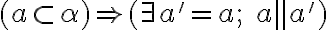 .
.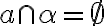 :
:
Nech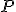
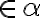 je bod ľubovoľný bod. Keďže
je bod ľubovoľný bod. Keďže 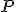
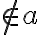 , tak existuje práve jedna rovina
, tak existuje práve jedna rovina 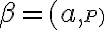
a priesečnica
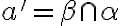 ,
,
pričom bude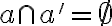 . V opačnom prípade by existoval bod
. V opačnom prípade by existoval bod 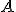
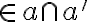 ,
ktorý by bol spoločným bodom priamky
,
ktorý by bol spoločným bodom priamky  a roviny
a roviny 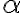 .
.
To je spor s predpokladom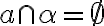 . Záver:
. Záver: 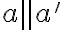 .
.
Otvorte si applet Tu
- postačujúca podmienka -
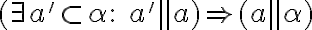 . Môžu nastať dva prípady pre vzájomnú polohu priamok
. Môžu nastať dva prípady pre vzájomnú polohu priamok 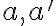 :
:
Dôkazy týchto tvrdení nájdete v práci Klenková: Stereometria. Na cvičení ich budete prezentovať.
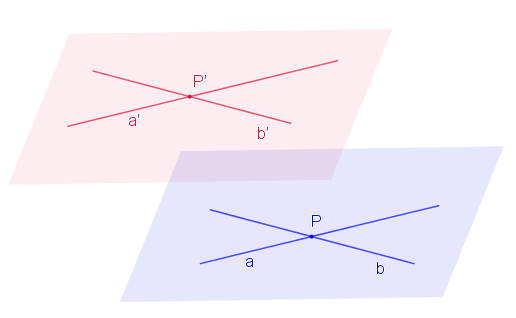
Kritérium rovnobežnosti dvoch rovín
Dve roviny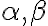 sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky
sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky 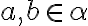 , ktoré sú rovnobežné s druhou rovinou
, ktoré sú rovnobežné s druhou rovinou 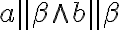 . Symbolicky
. Symbolicky
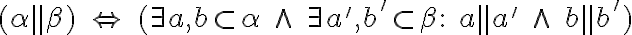 .
.
Dve roviny
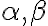 sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky
sú rovnobežné práve vtedy, ak jedna z nich obsahuje dve rôznobežky 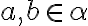 , ktoré sú rovnobežné s druhou rovinou
, ktoré sú rovnobežné s druhou rovinou 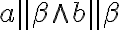 . Symbolicky
. Symbolicky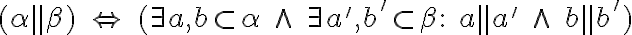 .
.
Dôkaz
- Nutná podmienka -
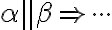 . Môžu nastať dva prípady:
. Môžu nastať dva prípady:
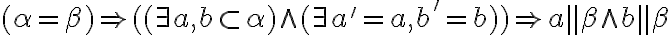 .
.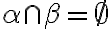 : Potom existujú rôznobežky
: Potom existujú rôznobežky 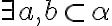 , pre ktoré platí
, pre ktoré platí
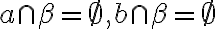 . Ak by tieto prieniky neboli prázdne množiny, tak by aj
. Ak by tieto prieniky neboli prázdne množiny, tak by aj
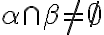 , čo je spor s predpokladom.
, čo je spor s predpokladom.
 . Otvorte si applet
Tu
. Otvorte si applet
Tu
- postačujúca podmienka -
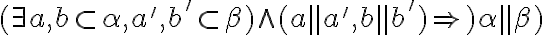 . Teoreticky môžu nastať tri prípady:
. Teoreticky môžu nastať tri prípady:
- ak
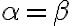 , tak z definície
, tak z definície 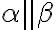 ;
; - ak
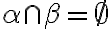 , tak z definície
, tak z definície 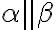 ;
; - prípad
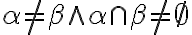 nemôže nastať. Ak by nastal bol by v spore s existenciou
dvojíc priamok:
nemôže nastať. Ak by nastal bol by v spore s existenciou
dvojíc priamok: 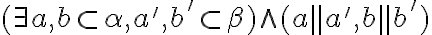 . Dokážeme to nepriamo:
. Dokážeme to nepriamo:
Nech existujú rôznobežky
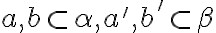
s požadovanou vlastnosťou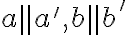 a nech roviny
a nech roviny 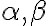 majú spoločnú priamku
majú spoločnú priamku
 :
: 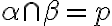 .
.
Táto priamka pretína aspoň jednu rôznobežku
pretína aspoň jednu rôznobežku  (môže byť rovnobežná najviac s jednou z nich).
Nech je to priamka
(môže byť rovnobežná najviac s jednou z nich).
Nech je to priamka  . Označme
. Označme 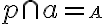 . To ale znamená, že bod
. To ale znamená, že bod 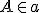 by ležal
v rovine
by ležal
v rovine  a zároveň v rovine
a zároveň v rovine 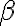 , lebo
, lebo 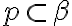 . To je spor s predpokladom
. To je spor s predpokladom 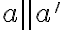 , keďže
, keďže 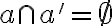 .
.
- ak
... ...
Vzájomná poloha rovín
Dohovor
Ak sa medzi skúmanou trojicou rovín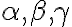 vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme
vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme 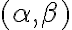 (lexikografický prístup).
(lexikografický prístup).
To neznamená, že dvojicou rovnobežných rovín nemôže byť dvojica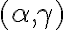 alebo
alebo 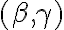 .
.
Ak sa medzi skúmanou trojicou rovín
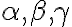 vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme
vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme 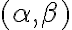 (lexikografický prístup).
(lexikografický prístup).
To neznamená, že dvojicou rovnobežných rovín nemôže byť dvojica
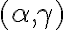 alebo
alebo 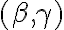 .
.
Klasifikácia vzájomnej polohy troch rovín
-
Nech platí
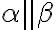 .
Pre rovinu
.
Pre rovinu 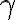 potom platí: alebo
potom platí: alebo 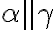 alebo
alebo 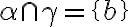
- Uvažujme o rovinách
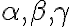 , pre ktoré
, pre ktoré 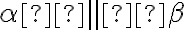 ,
, 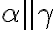 . Obrázok vľavo. Z tranzitívnosti relácie rovnobežnosti rovín vyplýva záver:
. Obrázok vľavo. Z tranzitívnosti relácie rovnobežnosti rovín vyplýva záver: 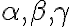 je trojica navzájom rôznych rovnobežných rovín.
je trojica navzájom rôznych rovnobežných rovín. - Nech platí:
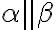 ∧
∧ 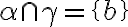 . Dôsledkom je rôznobežnosť rovín
. Dôsledkom je rôznobežnosť rovín 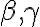 (v opačnom prípade by boli všetky tri roviny navzájom rovnobežné, čo je spor s predpokladom).
Je zrejmé, že priesečnice dvojíc rovín
(v opačnom prípade by boli všetky tri roviny navzájom rovnobežné, čo je spor s predpokladom).
Je zrejmé, že priesečnice dvojíc rovín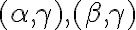 sú navzájom rovnobežné priamky. (Odôvodnite.)
Záver: Roviny
sú navzájom rovnobežné priamky. (Odôvodnite.)
Záver: Roviny 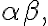 sú navzájom rovnobežné a rovina
sú navzájom rovnobežné a rovina 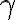 ich pretína v dvoch navzájom rovnobežných priamkach
ich pretína v dvoch navzájom rovnobežných priamkach 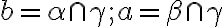 . Obr. vpravo.
. Obr. vpravo. - Nech platí:
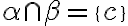 .
Skúmajme vzájomnú polohu priamky
.
Skúmajme vzájomnú polohu priamky  s rovinou
s rovinou 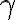 . Môže nastať práve jeden z prípadov:
(
. Môže nastať práve jeden z prípadov:
(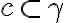 alebo
alebo 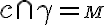 alebo
alebo 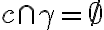 .
.
Tvrdenie. Existuje päť vzájomných polôh troch navzájom rôznych rovín:
- všetky tri roviny sú navzájom rovnobežné
- dve rovnobežné roviny pretína tretia v navzájom rovnobežných priamkach
- všetky tri roviny majú spoločnú práve jednu priamku (os zväzku rovín)
- všetky tri roviny majú spoločný práve jeden bod
- všetky dvojice rovín sú navzájom rôznobežné roviny a ich priesečnice sú navzájom rôzne rovnobežné priamky.
______________________________________________________________
Obrázky sú prevzaté z publikácie
Klenková, P.: Stereometria – elementárna geometria trojrozmerného euklidovského priestoru, Diplomová práca, UK FMFI, Bratislava 2006
Obrázky sú prevzaté z publikácie
Klenková, P.: Stereometria – elementárna geometria trojrozmerného euklidovského priestoru, Diplomová práca, UK FMFI, Bratislava 2006
... ...
Metrické vzťahy
Medzi základné metrické pojmy zaraďujeme
- uhol - dvoch priamok, priamky a roviny a dvojice rovín.
- kolmosť - dvoch priamok, kolmosť priamky a roviny a kolmosť dvojice rovín, kritériá kolmosti
- vzdialenosť- dvoch geometrických útvarov.
Definícia
Uhol mimobežných priamok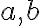 je uhol zhodný s uhlom ľubovoľných dvoch rôznobežiek
je uhol zhodný s uhlom ľubovoľných dvoch rôznobežiek 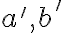 , pričom
, pričom 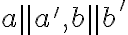 .
.
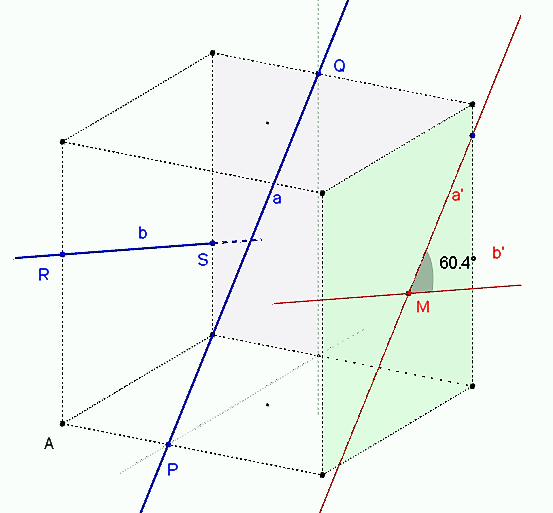 Otvorte si zadanie Tu ...
Otvorte si zadanie Tu ...
V applete posúvaním bodov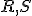 vytvorte takú polohu mimobežiek, aby boli na seba kolmé.
vytvorte takú polohu mimobežiek, aby boli na seba kolmé.
Uhol mimobežných priamok
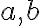 je uhol zhodný s uhlom ľubovoľných dvoch rôznobežiek
je uhol zhodný s uhlom ľubovoľných dvoch rôznobežiek 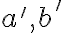 , pričom
, pričom 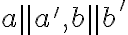 .
.
 Otvorte si zadanie Tu ...
Otvorte si zadanie Tu ...
V applete posúvaním bodov
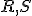 vytvorte takú polohu mimobežiek, aby boli na seba kolmé.
vytvorte takú polohu mimobežiek, aby boli na seba kolmé.
Aby bola definícia korektná, dokážeme najprv nezávislosť takto definovaného uhla od výberu dvojice
rôznobežiek 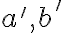 .
.
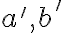 .
.
Tvrdenie
Nech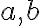 sú dve ľubovoľné mimobežky a nech
sú dve ľubovoľné mimobežky a nech 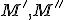 sú dva body
sú dva body 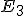 . Zostrojme priamky
. Zostrojme priamky 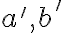 a
a 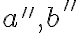 tak,
aby
tak,
aby 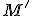
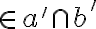 a
a 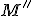
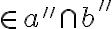 a zároveň
a zároveň 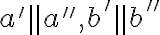 . Potom platí:
. Potom platí: 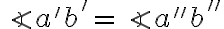 .
.
Nech
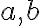 sú dve ľubovoľné mimobežky a nech
sú dve ľubovoľné mimobežky a nech 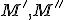 sú dva body
sú dva body 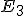 . Zostrojme priamky
. Zostrojme priamky 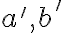 a
a 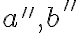 tak,
aby
tak,
aby 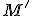
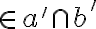 a
a 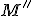
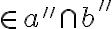 a zároveň
a zároveň 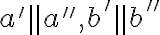 . Potom platí:
. Potom platí: 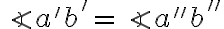 .
.
Dôkaz
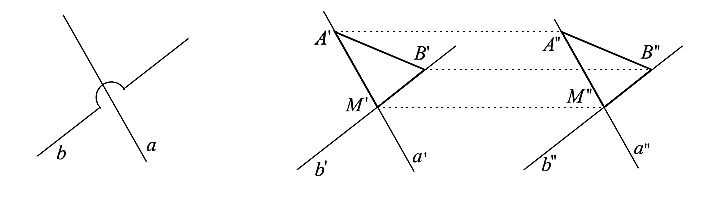
Zvoľme si dva rôzne body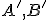 incidentné s rovnomennými priamkami tak, aby
incidentné s rovnomennými priamkami tak, aby 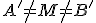 . Pozri obrázok nižšie. Ďalej zostrojme body
. Pozri obrázok nižšie. Ďalej zostrojme body 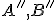 tak, aby útvary
tak, aby útvary 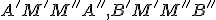 boli rovnobežníky. Je zrejmé, že aj útvar
boli rovnobežníky. Je zrejmé, že aj útvar 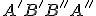 je rovnobežníkom a
trojuholníky
je rovnobežníkom a
trojuholníky 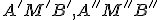 sú zhodné (veta sss). Preto sa zhodujú vo všetkých uhloch.
sú zhodné (veta sss). Preto sa zhodujú vo všetkých uhloch.
Zvoľme si dva rôzne body
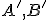 incidentné s rovnomennými priamkami tak, aby
incidentné s rovnomennými priamkami tak, aby 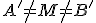 . Pozri obrázok nižšie. Ďalej zostrojme body
. Pozri obrázok nižšie. Ďalej zostrojme body 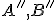 tak, aby útvary
tak, aby útvary 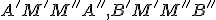 boli rovnobežníky. Je zrejmé, že aj útvar
boli rovnobežníky. Je zrejmé, že aj útvar 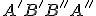 je rovnobežníkom a
trojuholníky
je rovnobežníkom a
trojuholníky 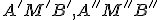 sú zhodné (veta sss). Preto sa zhodujú vo všetkých uhloch.
sú zhodné (veta sss). Preto sa zhodujú vo všetkých uhloch.
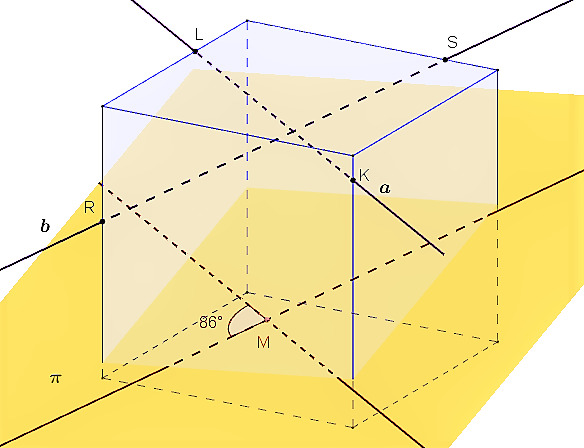
Definícia
- Uhlom priamok
 nazývame uhol ľubovoľných dvoch nedisjunktných priamok
nazývame uhol ľubovoľných dvoch nedisjunktných priamok 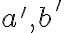 , pre ktoré platí:
, pre ktoré platí: 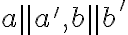 .
Uhol dvoch rovnobežiek nazývame nulovým uhlom.
.
Uhol dvoch rovnobežiek nazývame nulovým uhlom.
 Otvorte si applet Tu
Otvorte si applet Tu - Kolmé priamky nazývame také priamky, ktorých uhol je pravý.
- Priamka kolmá na rovinu [hovoríme aj kolmica na rovinu] je priamka kolmá na všetky priamky roviny.
Dôsledok
- Priamka kolmá na rovinu je s touto rovinou rôznobežná.
- Priamka kolmá na dve rôznobežky danej roviny je s touto rovinou rôznobežná.
________________________________________________________________
1) Euklidove Základy, Kniha 1,Tvrdenie XI a XII.
1) Euklidove Základy, Kniha 1,Tvrdenie XI a XII.
...
Kritérium kolmosti
Tvrdenie - kritérium kolmosti priamky a roviny.
Priamka je kolmá na rovinu práve vtedy, keď je kolmá na dve rôznobežné priamky tejto roviny.
Priamka je kolmá na rovinu práve vtedy, keď je kolmá na dve rôznobežné priamky tejto roviny.
Dôkaz
- Nutnosť (
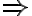 ). Predpokladajme, že
). Predpokladajme, že 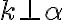 . Z kolmosti priamky
. Z kolmosti priamky  na všetky priamky roviny (definícia)
vyplýva jej kolmosť na ľubovoľné dve jej rôznobežky.
na všetky priamky roviny (definícia)
vyplýva jej kolmosť na ľubovoľné dve jej rôznobežky.
- Dostatočnosť
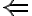 ). Nech priamka
). Nech priamka 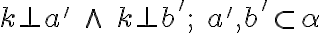 . Treba dokázať, že priamka k je kolmá na všetky priamky danej roviny.
Zvoľme si ľubovoľnú priamku
. Treba dokázať, že priamka k je kolmá na všetky priamky danej roviny.
Zvoľme si ľubovoľnú priamku 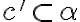 .
.
Podľa predchádzajúceho dôsledku je priamka s rovinou
s rovinou  rôznobežná.
Označme
rôznobežná.
Označme 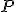 ich spoločný bod a zostrojme priamky
ich spoločný bod a zostrojme priamky 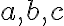 prechádzajúce týmto bodom a rovnobežné s priamkami
prechádzajúce týmto bodom a rovnobežné s priamkami 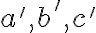 .
Stačí dokázať:
.
Stačí dokázať: 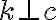 (prečo? vysvetlite).
(prečo? vysvetlite).
Otvorte si applet Tu
Zvoľme si ľubovoľné body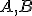 ležiace na rovnomenných priamkach tak, aby priamka
ležiace na rovnomenných priamkach tak, aby priamka 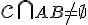 .
Označme
.
Označme 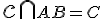 . Ďalej nech sú
. Ďalej nech sú 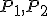 ľubovoľné dva body, pre ktoré je bod
ľubovoľné dva body, pre ktoré je bod 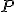 je stredom úsečky
je stredom úsečky 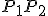 .
.
Potom platí: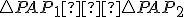 a
a 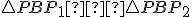 (sus)
(sus)
odkiaľ dostávame zhodnosť úsečiek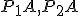 resp.
resp. 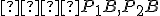 . Preto platí
. Preto platí
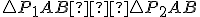 (sss)
(sss)
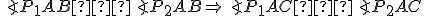 .
.
Dôsledkom je zhodnosť trojuholníkov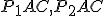 (sus), teda i zhodnosť úsečiek
(sus), teda i zhodnosť úsečiek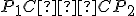 .
.
Preto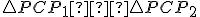 (sss), čo znamená, že sú zhodné i uhly v týchto trojuholníkoch pri vrchole
(sss), čo znamená, že sú zhodné i uhly v týchto trojuholníkoch pri vrchole  .
Pretože ide o susedné uhly, sú oba uhly pravé, t.j. priamka
.
Pretože ide o susedné uhly, sú oba uhly pravé, t.j. priamka  je kolmá na priamku
je kolmá na priamku  .
.
Poznámky.
- Kolmosť dvoch priamok je relácia symetrická ale nie je reflexívna ani tranzitívna.
- Kritérium kolmosti priamky a roviny vyjadruje nevyhnutnú a dostačujúcu podmienku kolmosti priamky a roviny, ale nehovorí nič o existencii takejto priamky. Existencia priamky kolmej na rovinu je dôsledkom nasledujúceho nasledujúcom tvrdenia.
- Namiesto vyjadrenia „priamka je kolmá na rovinu“ budeme tiež používať vyjadrenie „rovina je kolmá na priamku“. Analogicky ako v a) budeme hovoriť, že priamka a rovina sú navzájom kolmé.
Tvrdenie - existencia priamky kolmej na rovinu.
Existuje práve jedna priamka prechádzajúca daným bodom M a kolmá na danú rovinu α .
Existuje práve jedna priamka prechádzajúca daným bodom M a kolmá na danú rovinu α .
Dôkaz
- Existencia priamky kolmej na na priamku vyplýva z Euklidových tvrdení T/XI a T/XII zo Základov, Kniha 1. Existencia kolmice na rovinu sa dá zdôvodniť z týchto tvrdení a konštrukcie uvedenej v nasledujúcom applete.
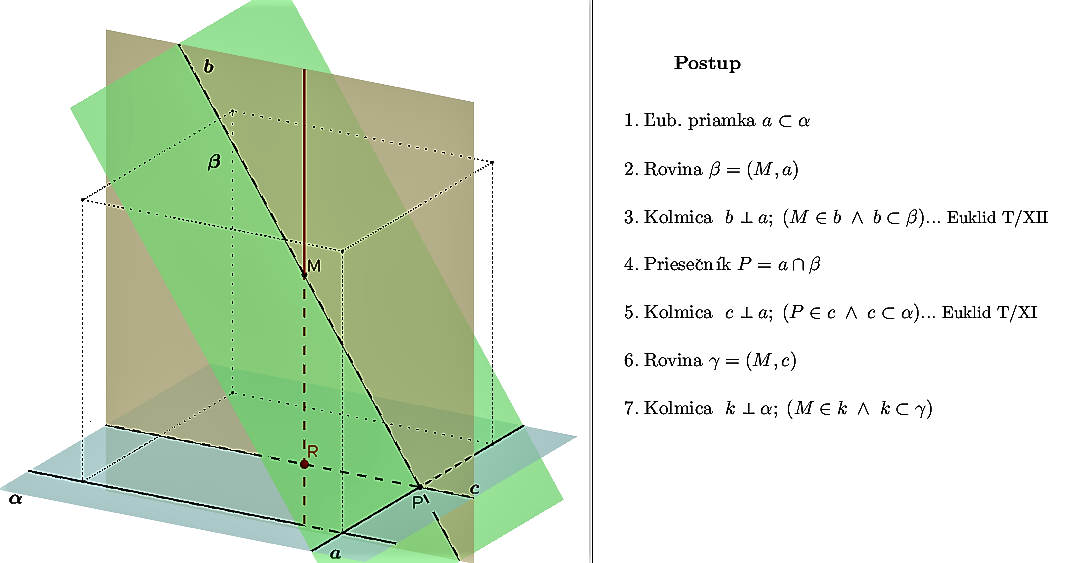 Applet Tu
Applet Tu - Jednoznačnosť takej kolmice dokážeme nepriamo s vyžitím obrázka
Ak by existovali dve navzájom rôzne priamky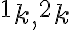 požadovanej vlastnosti, tak by ich priesečníky
požadovanej vlastnosti, tak by ich priesečníky 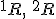 s rovinou
s rovinou  boli navzájom rôzne body a
trojuholník
boli navzájom rôzne body a
trojuholník 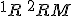 by bol trojuholníkom s dvoma pravými uhlami, čo je spor s vetou o súčte vnútorných uhlov v trojuholníku euklidovskej roviny.
by bol trojuholníkom s dvoma pravými uhlami, čo je spor s vetou o súčte vnútorných uhlov v trojuholníku euklidovskej roviny.
Tvrdenie - existencia roviny kolmej na priamku.
Existuje práve jedna rovina prechádzajúca daným bodom M a kolmá na danú priamku m.
Existuje práve jedna rovina prechádzajúca daným bodom M a kolmá na danú priamku m.
Dôkaz - analogický (konštrukčný) ako v predchádzajúcom tvrdení
Dôsledok
Dve roviny kolmé na tú istú priamku sú navzájom rovnobežné.
Dve roviny kolmé na tú istú priamku sú navzájom rovnobežné.
...
Vzdialenosť útvarov
Nech  je kolmica na rovinu
je kolmica na rovinu  .
Priesečník
.
Priesečník 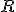 kolmice s danou rovinou nazveme päta kolmice.
kolmice s danou rovinou nazveme päta kolmice.
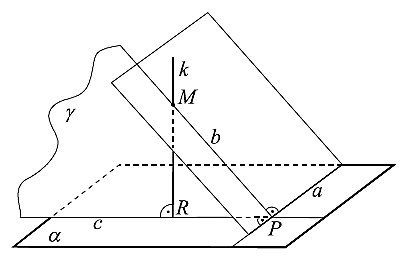
Ak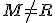 , tak na základe vlastnosti pravouhlého trojuholníka
, tak na základe vlastnosti pravouhlého trojuholníka 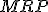 platí: prepona je väčšia ako odvesna, symbolicky
platí: prepona je väčšia ako odvesna, symbolicky
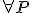
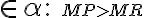 .
.
To nám umožňuje zaviesť nasledujúcu definíciu vzdialenosti bodu od roviny.
 je kolmica na rovinu
je kolmica na rovinu  .
Priesečník
.
Priesečník 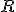 kolmice s danou rovinou nazveme päta kolmice.
kolmice s danou rovinou nazveme päta kolmice.
Ak
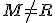 , tak na základe vlastnosti pravouhlého trojuholníka
, tak na základe vlastnosti pravouhlého trojuholníka 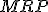 platí: prepona je väčšia ako odvesna, symbolicky
platí: prepona je väčšia ako odvesna, symbolicky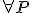
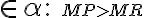 .
.
To nám umožňuje zaviesť nasledujúcu definíciu vzdialenosti bodu od roviny.
Definícia.
-
Vzdialenosť bodu
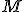 od roviny
od roviny  je dĺžka úsečky
je dĺžka úsečky 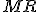 , kde bod
, kde bod 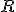 je päta kolmice z bodu
je päta kolmice z bodu 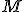 na rovinu
na rovinu  .
. -
Pod vzdialenosťou dvoch geometrických útvarov
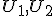 sa rozumie najmenšia z úsečiek
sa rozumie najmenšia z úsečiek 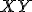 (alebo dĺžka tejto úsečky)
pre
(alebo dĺžka tejto úsečky)
pre 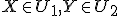 .
. - Vzdialenosťou dvoch rovnobežných rovín nazývame vzdialenosť ľubovoľného bodu jednej z rovín od druhej roviny.
Dôsledky.
Cvičenie - vzdialenosť bodov. Pozrite si prácu "Sbírka úloh STEREOMETRIE" Tu.
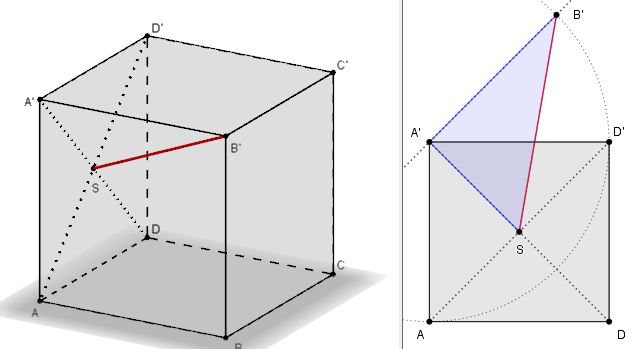
- V kocke
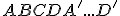 určte konštrukčne i výpočtom vzdialenosť vzdialenosť bodov
určte konštrukčne i výpočtom vzdialenosť vzdialenosť bodov 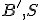 , kde
, kde 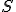 je stred ľavej
bočnej steny
je stred ľavej
bočnej steny 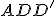 .
.
- V kvádre
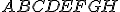 s dĺžkami hrán
s dĺžkami hrán 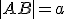 ,
, 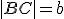 ,
, 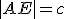 vypočítajte vzdialenosť bodov
vypočítajte vzdialenosť bodov 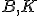 , kde
, kde 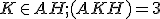 . Zostrojte si najskôr hranol v GeoGebre 3D.
zadanie Tu
. Zostrojte si najskôr hranol v GeoGebre 3D.
zadanie Tu
Cvičenie - vzdialenosť bodu od priamky.
- V kocke
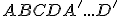 určte konštrukčne i výpočtom vzdialenosť vzdialenosť bodu
určte konštrukčne i výpočtom vzdialenosť vzdialenosť bodu 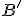 od priamky
od priamky 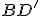 resp.
resp. 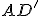 .
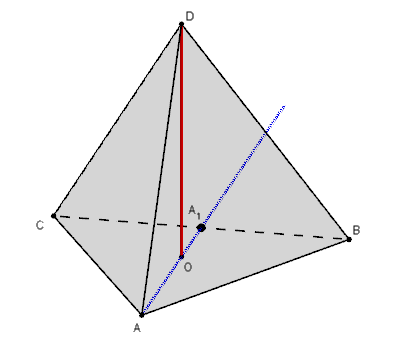
. - V pravidelnom štvorbokom ihlane
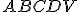 vypočítajte vzdialenosť bodu
vypočítajte vzdialenosť bodu 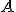 od priamky
od priamky 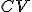 .
. - V kvádre
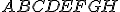 s dĺžkami hrán
s dĺžkami hrán 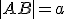 ,
, 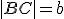 ,
, 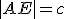 vypočítajte vzdialenosť bodu
vypočítajte vzdialenosť bodu 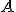 od telesovej uhlopriečky
od telesovej uhlopriečky 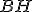 .
. - Daný je pravidelný štvorsten
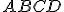 o hrane dĺžky
o hrane dĺžky 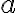 , označte
, označte  ťažisko steny
ťažisko steny 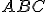 . Určte vzdialenosť
všetkých jeho vrcholov od polpriamky
. Určte vzdialenosť
všetkých jeho vrcholov od polpriamky 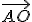 .
.
Cvičenie - vzdialenosť bodu od roviny.
- V kocke
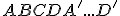 určte konštrukčne i výpočtom vzdialenosť vrcholu
určte konštrukčne i výpočtom vzdialenosť vrcholu 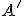 od roviny
od roviny 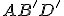 .
. - Vypočítajte výšku pravidelného štvorstenu
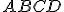 s dĺžkou hrany
s dĺžkou hrany 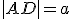 .
. - V pravidelnom štvorbokom ihlane
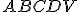 vypočítajte vzdialenosť stredu postavy od roviny jeho pobočnej steny, ak je dané
vypočítajte vzdialenosť stredu postavy od roviny jeho pobočnej steny, ak je dané 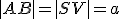 |.
|. - Daný je pravidelný štvorsten
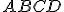 o hrane dĺžky
o hrane dĺžky 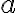 , označte
, označte  ťažisko steny
ťažisko steny 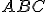 . Určte vzdialenosti
. Určte vzdialenosti
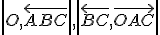 .
.
Popis konštrukcie a výpočet pre (i):
Vzdialenosť bodu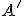 od roviny
od roviny 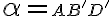 sa rovná dĺžke úsečky
sa rovná dĺžke úsečky 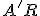 , kde
, kde 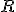 je
päta kolmice z bodu
je
päta kolmice z bodu 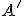 na rovinu
na rovinu  .
.
Keďže telesová uhlopriečka kocky je kolmá na všetky jej stenové uhlopriečky, s ktorými nie je rôznobežná (dokážte to), tak priamka prechádzajúca bodom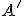 a kolmá na rovinu
a kolmá na rovinu  je telesová uhlopriečka
je telesová uhlopriečka 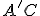 .
.
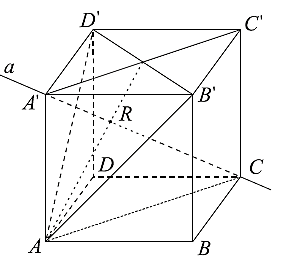 Riešenie Tu. Vyriešte konštrukčne - zadanie Tu.
Riešenie Tu. Vyriešte konštrukčne - zadanie Tu.
Zrejme päta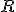 kolmice
kolmice 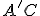 na rovinu
na rovinu 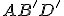 (rovnostranný trojuholník) je ortocentrom a zároveň ťažiskom trojuholníka
(rovnostranný trojuholník) je ortocentrom a zároveň ťažiskom trojuholníka 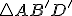 .
Ďalej platí
.
Ďalej platí 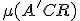
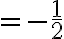 . Odkiaľ vyplýva:
. Odkiaľ vyplýva: 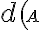
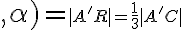
![= \frac{a \sqrt[]{3} }{3} = \frac{a \sqrt[]{3} }{3}](https://lms.umb.sk/filter/tex/pix.php/fd40495dba0c8fdd2d829e858680c03b.png) .
.
Vzdialenosť bodu
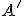 od roviny
od roviny 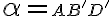 sa rovná dĺžke úsečky
sa rovná dĺžke úsečky 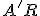 , kde
, kde 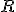 je
päta kolmice z bodu
je
päta kolmice z bodu 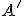 na rovinu
na rovinu  .
.
Keďže telesová uhlopriečka kocky je kolmá na všetky jej stenové uhlopriečky, s ktorými nie je rôznobežná (dokážte to), tak priamka prechádzajúca bodom
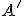 a kolmá na rovinu
a kolmá na rovinu  je telesová uhlopriečka
je telesová uhlopriečka 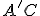 .
.
Zrejme päta
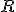 kolmice
kolmice 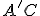 na rovinu
na rovinu 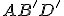 (rovnostranný trojuholník) je ortocentrom a zároveň ťažiskom trojuholníka
(rovnostranný trojuholník) je ortocentrom a zároveň ťažiskom trojuholníka 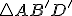 .
Ďalej platí
.
Ďalej platí 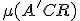
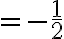 . Odkiaľ vyplýva:
. Odkiaľ vyplýva: 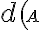
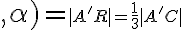
![= \frac{a \sqrt[]{3} }{3} = \frac{a \sqrt[]{3} }{3}](https://lms.umb.sk/filter/tex/pix.php/fd40495dba0c8fdd2d829e858680c03b.png) .
.Uhol útvarov
Uhol dvoch priamok sme definovali ako uhol dvoch ľubovoľných nedisjunktných priamok rovnobežných s danými priamkami.
Pri uhla priamky a rovinou budeme potrebovať pojem kolmého priemetu priamky do roviny.
Nech je priamka, ktorá nie je kolmá na danú rovinu
je priamka, ktorá nie je kolmá na danú rovinu  . Nech
. Nech 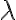 je rovina kolmá na danú rovinu
je rovina kolmá na danú rovinu  , ktorá prechádza
priamkou
, ktorá prechádza
priamkou 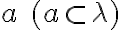 . Rovinu
. Rovinu 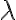 budeme nazývať kolmo premietajúca rovina priamky
budeme nazývať kolmo premietajúca rovina priamky  .
Priesečnicu
.
Priesečnicu 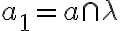 nazveme kolmý priemet priamky do roviny.
nazveme kolmý priemet priamky do roviny.
Nech
 je priamka, ktorá nie je kolmá na danú rovinu
je priamka, ktorá nie je kolmá na danú rovinu  . Nech
. Nech 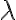 je rovina kolmá na danú rovinu
je rovina kolmá na danú rovinu  , ktorá prechádza
priamkou
, ktorá prechádza
priamkou 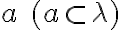 . Rovinu
. Rovinu 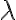 budeme nazývať kolmo premietajúca rovina priamky
budeme nazývať kolmo premietajúca rovina priamky  .
Priesečnicu
.
Priesečnicu 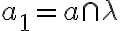 nazveme kolmý priemet priamky do roviny.
nazveme kolmý priemet priamky do roviny.
Definície
Poznámky
- Uhol dvoch rovnobežných rovín nazývame nulový uhol.
- O rovinách, ktorých uhol je zhodný s pravým uhlom hovoríme, že sú navzájom kolmé.
Tvrdenie
Uhol priamky s rovinou je zhodný s doplnkovým uhlom k uhlu priamky s kolmicou na túto rovinu.
Dôsledok
Uhol dvoch rovín je zhodný s uhlom priamok kolmých na tieto roviny.
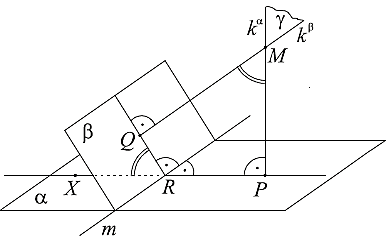
Obr. prevzatý z práce Klenková P., Stereometria, 2006
Uhol dvoch rovín je zhodný s uhlom priamok kolmých na tieto roviny.
Obr. prevzatý z práce Klenková P., Stereometria, 2006
Tvrdenie - kritérium kolmosti rovín
Dve roviny sú na seba kolmé práve vtedy, ak jedna z rovín obsahuje priamku kolmú na druhú rovinu.
(Takúto priamku obsahuje prirodzene každá z rovín na seba kolmých. Stačí, ak jedna z rovín je rovnobežná s priamkou kolmou na zvyšnú rovinu.)
Dve roviny sú na seba kolmé práve vtedy, ak jedna z rovín obsahuje priamku kolmú na druhú rovinu.
(Takúto priamku obsahuje prirodzene každá z rovín na seba kolmých. Stačí, ak jedna z rovín je rovnobežná s priamkou kolmou na zvyšnú rovinu.)
...
Objemy a povrchy telies
Definícia.
Poznámka.
Podrobný komentár k jednotlivým symbolom nájdete na stránke "Calculator" Tu.
Podrobný komentár k jednotlivým symbolom nájdete na stránke "Calculator" Tu.
Cvičenie.
Určte objem rotačného telesa, ktoré vznikne otáčaním
Určte objem rotačného telesa, ktoré vznikne otáčaním
Seminárne zadania
Dokážte tvrdenia
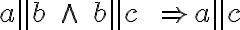
dôkaz Tu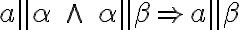
dôkaz si pripraví: študent/ka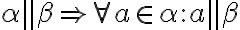
dôkaz si pripraví: študent/ka-
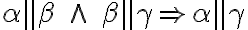
dôkaz: DU
Dôkazy týchto tvrdení nájdete v práci
Klenková: Stereometria.
Na seminári ich budete prezentovať.
Cvičenie
-
Zostrojte pravidelný trojboký hranol
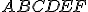 , ktorého steny sú pravouholníky. Zadanie otvoríte Tu.
, ktorého steny sú pravouholníky. Zadanie otvoríte Tu. - Určte vzájomnú polohu priamky a s pravidelným šesťbokým hranolom
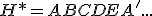 , ktorého výška je zhodná s hlavnou uhlopriečkou podstavy.
V prípade existencie prieniku zostrojte úsečku zhodnú s prienikom (pri zvolenej dĺžke podstavnej hrany telesa). Hranol
Tu
, ktorého výška je zhodná s hlavnou uhlopriečkou podstavy.
V prípade existencie prieniku zostrojte úsečku zhodnú s prienikom (pri zvolenej dĺžke podstavnej hrany telesa). Hranol
Tu
[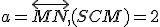 (
( je stred podstavy
je stred podstavy 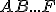 ),
), 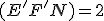 ]
] - Daná je kocka
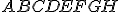 , kde
, kde 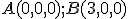 . Ďalej sú dané stredy hrán hornej podstavy
. Ďalej sú dané stredy hrán hornej podstavy 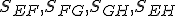 , stred hrany
, stred hrany 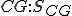 a body
a body 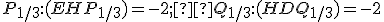 .
.
a) Určte vzájomnú polohu b) Pomocou vrcholov zapíšte 3 rôzne roviny kolmé na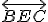 .
Zadanie Tu.
.
Zadanie Tu.
- Konštrukčne i výpočtom určite vzdialenosť stredu steny
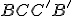 kocky
kocky 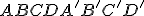 od roviny
od roviny 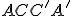 . Kocku si otvorte vo VRP si otvoríte Tu. Kocku v 3D si otvorte Tu.
. Kocku si otvorte vo VRP si otvoríte Tu. Kocku v 3D si otvorte Tu. -
Daný je kváder
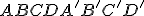 . Zostrojte rez kvádra s rovinou
. Zostrojte rez kvádra s rovinou 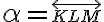 a útvar zhodný s rezovým
a útvar zhodný s rezovým  -uholníkom, ak:
-uholníkom, ak:
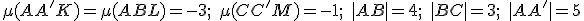 . Kváder vo VRP Tu. Urobte riešenie aj v 3D, najskôr si taký kváder vytvorte.
. Kváder vo VRP Tu. Urobte riešenie aj v 3D, najskôr si taký kváder vytvorte. -
Daný je rovnobežnosten
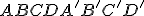 . Zostrojte priesečník priamky
. Zostrojte priesečník priamky 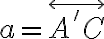 s rovinou
s rovinou 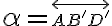 .
Určte deliaci pomer
.
Určte deliaci pomer 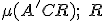
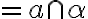 . Zadanie - rovnobežnosten Tu.
. Zadanie - rovnobežnosten Tu. -
Daný je pravidelný šesťboký ihlan
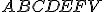 . Určte uhol priamok
. Určte uhol priamok 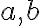 , ak
, ak 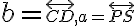 pre
pre 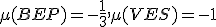 . Zadanie - šesťboký ihlan Tu
. Zadanie - šesťboký ihlan Tu -
Určite vzájomnú polohu priamky a s pravidelným šesťbokým hranolom
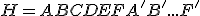 , ktorého výška je zhodná s hlavnou uhlopriečkou podstavy.
V prípade existencie prieniku (úsečka
, ktorého výška je zhodná s hlavnou uhlopriečkou podstavy.
V prípade existencie prieniku (úsečka 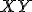 zostrojte úsečku zhodnú s prienikom (pri zvolenej dĺžke podstavnej hrany telesa).
zostrojte úsečku zhodnú s prienikom (pri zvolenej dĺžke podstavnej hrany telesa).
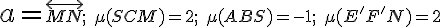 .
.
- DU. Konštrukčne i výpočtom určite vzdialenosť vrcholu
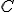 kocky od roviny
kocky od roviny 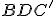 . Dĺžku hrany kocky si zvoľte ľubovoľne.
. Dĺžku hrany kocky si zvoľte ľubovoľne.
- DU. Daný je kváder
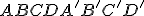 . Zostrojte rez kvádra s rovinou
. Zostrojte rez kvádra s rovinou 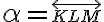 a útvar zhodný s rezovým
a útvar zhodný s rezovým  -uholníkom, ak:
-uholníkom, ak:
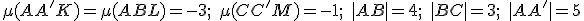 . Kváder Tu.
. Kváder Tu. - Klenková - Stereometria, Cvičenia 1 až 15, Str. 38 až 40.; príklady 4.5 až 4.8, Str. 61 až 63; Cvičenia na str. 64