Kruh, kružnica - cvičenia
Kruh
Seminárne zadania
Cvičenie.
- Vypočítajte veľkosti vnútorných uhlov v trojuholníku, ktorý dostanete ak spojíte na ciferníku hodiniek body vyznačujúce čísla 3, 8, 10. Zadanie Tu
- V tetivovom štvoruholníku
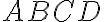 , platí
, platí
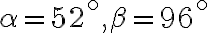 . Vyjadrite veľkosti zostávajúcich vnútorných uhlov tohto štvoruholníka. Zadanie Tu
. Vyjadrite veľkosti zostávajúcich vnútorných uhlov tohto štvoruholníka. Zadanie Tu
- Daný je trojuholník a kružnica k so stredom
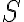 , vpísaná do trojuholníka. Body dotyku kružnice k so stranami trojuholníka sú označené
, vpísaná do trojuholníka. Body dotyku kružnice k so stranami trojuholníka sú označené
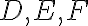 . Veľkosť uhla
. Veľkosť uhla
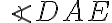 je 32°. Akú veľkosť má uhol
je 32°. Akú veľkosť má uhol 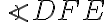 ?
?
Zadanie
-
Je daná kružnica
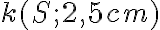 a jej dotyčnica
a jej dotyčnica
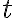 . Zostrojte všetky kružnice, ktoré sa dotýkajú kružnice
. Zostrojte všetky kružnice, ktoré sa dotýkajú kružnice
 tak aj priamky
tak aj priamky
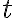 a majú pritom polomer
a majú pritom polomer
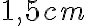 . Zadanie
Tu
. Zadanie
Tu
- Je daná kružnica
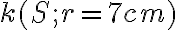 a bod
a bod
 , pre ktorý platí
, pre ktorý platí
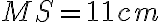 . Zostrojte takú sečnicu
. Zostrojte takú sečnicu
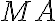 kružnice
kružnice
 prechádzajúcu bodom
prechádzajúcu bodom
 , aby jeden jej druhý priesečník
, aby jeden jej druhý priesečník
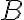 bol stredom úsečky
bol stredom úsečky
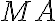 .
. - Kružnica je rozdelená na dva oblúky tak, že obvodový uhol príslušný k väčšiemu oblúku je rovný stredovému uhlu príslušnému k menšiemu oblúku. Určite veľkosť obvodových uhlov príslušných k obom oblúkom.
-
 je menší oblúk kružnice s obvodovým uhlom
je menší oblúk kružnice s obvodovým uhlom
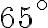 . V bodoch
. V bodoch
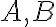 sú zostrojené dotyčnice kružnice a bod
sú zostrojené dotyčnice kružnice a bod
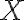 je ich priesečník. Vypočítajte veľkosť uhla
je ich priesečník. Vypočítajte veľkosť uhla
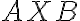 .
. -
Zostrojte kružnicu, ktorá sa dotýka danej priamky
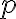 a prechádza dvoma rôznymi bodmi
a prechádza dvoma rôznymi bodmi  , ktoré neležia na priamke a
priamky
, ktoré neležia na priamke a
priamky 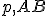 sú rôznobežné. Úlohu riešte pomocou mocnosti bodu ku kružnici. Otvorte si zadanie Tu.
sú rôznobežné. Úlohu riešte pomocou mocnosti bodu ku kružnici. Otvorte si zadanie Tu. - Je daná kružnica
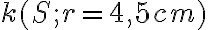 . Vnútri kružnice leží bod
. Vnútri kružnice leží bod  . Narysujte všetky kružnice s polomerom
. Narysujte všetky kružnice s polomerom 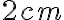 , ktoré sa dotýkajú kružnice
, ktoré sa dotýkajú kružnice  a prechádzajú bodom
a prechádzajú bodom  .
.
