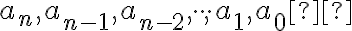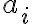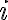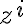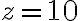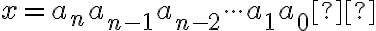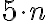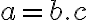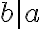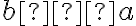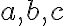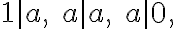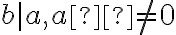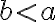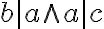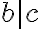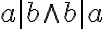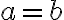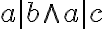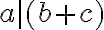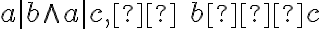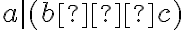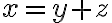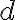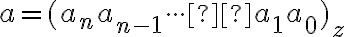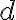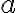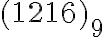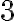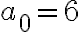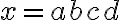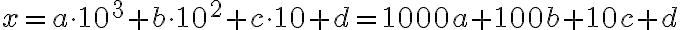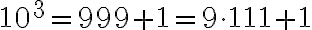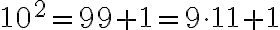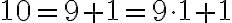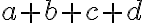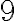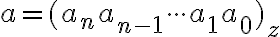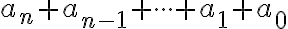G-adická číselná sústava
| Сайт: | Virtuálna Univerzita Mateja Bela |
| Курс: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Книга: | G-adická číselná sústava |
| Напечатано:: | Гость |
| Дата: | среда, 3 июля 2024, 12:32 |
Описание
Číselné sústavy
Úvod
V prehistorickej dobe vyjadrovali čísla pomocou vruboviek. Vo Věstoniciach bola nájdená vlčia kosť zo staršej doby kamennej, na ktorej bolo 55 usporiadaných vrypov.
V Zaire bola nájdená tyč z doby asi pred 10 000 rokmi, na ktorej už bolo zrejmé zoskupovanie vrypov.
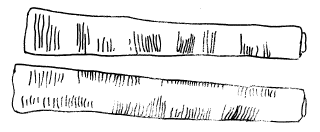
Aditívne nepozičné sústavy - každý znak mal svoju hodnotu a číslo sa určilo sčítaním hodnôt všetkých znakov. Nezáležalo na tom, v akom poradí sme znaky napísali.
Takáto sústava bola používaná napr. v starom Egypte →
V Zaire bola nájdená tyč z doby asi pred 10 000 rokmi, na ktorej už bolo zrejmé zoskupovanie vrypov.

Aditívne nepozičné sústavy - každý znak mal svoju hodnotu a číslo sa určilo sčítaním hodnôt všetkých znakov. Nezáležalo na tom, v akom poradí sme znaky napísali.
Takáto sústava bola používaná napr. v starom Egypte →
Veľmi skoro sa objavila myšlienka, aby pozícia znaku určovala aj jeho hodnotu. Tak sa začali objavovať pozičné sústavy.
Desiatková číselná sústava - označenie ľubovoľného prirodzeného čísla pomocou desiatich znakov
• objav indickej matematiky - jeden z najväčších objavov, ku ktorým ľudstvo vo svojich dejinách dospelo
• objav indickej matematiky - jeden z najväčších objavov, ku ktorým ľudstvo vo svojich dejinách dospelo
Na efektívne počítanie sa v minulosti (nie dávnej) používali počítadlá typu Abacus →

Drevoryt Gregora Reischa z roku 1504 (obr. 23) s názvom Margareta philosophica (Perla filozofia) ukazuje kontrast medzi výkonnosťou algoritmika vľavo (Boetius) a neschopnosťou abakistu vpravo (nešťastný Pytagoras).

Drevoryt Gregora Reischa z roku 1504 (obr. 23) s názvom Margareta philosophica (Perla filozofia) ukazuje kontrast medzi výkonnosťou algoritmika vľavo (Boetius) a neschopnosťou abakistu vpravo (nešťastný Pytagoras).
G-adická číselná sústava
Na nasledovnom príklade budeme ilustrovať podstatu vyjadrovanie čísel v číselných sústavách.
Príklad.
Zapíšte číslo 27 v číselnej sústave so základom 4 (v štvorkovej číselnej sústave).
Zapíšte číslo 27 v číselnej sústave so základom 4 (v štvorkovej číselnej sústave).
Najskôr žiakom ukážeme graficky, ako by sme zoskupovali "po štyroch" prvky ľubovoľnej množiny. Pozri obrázok.
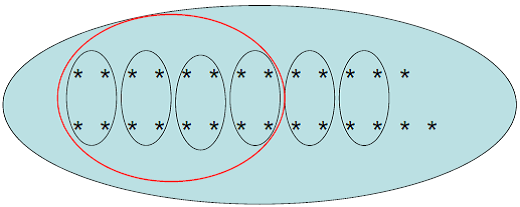
Na obrázku je dvadsaťsedem hviezdičiek, ktoré budeme zoskupovať do skupín po štyroch - číselná sústava so základom 4.
Vieme, že zápis počtu hviezdičiek znázornených na obrázku v desiatkovej sústave je 27 (dve desiatky a sedem jednotiek).
Zoskupovanie rozdelíme do dvoch krokov.

Na obrázku je dvadsaťsedem hviezdičiek, ktoré budeme zoskupovať do skupín po štyroch - číselná sústava so základom 4.
Vieme, že zápis počtu hviezdičiek znázornených na obrázku v desiatkovej sústave je 27 (dve desiatky a sedem jednotiek).
Zoskupovanie rozdelíme do dvoch krokov.
- Zoskupovanie po 4 hviezdičky. V tomto prípade dostaneme:
6 skupín po 4 hviezdičky a 3 hviezdičky zostanú nezoskupené ... zvyšok 3 po delení čísla 27 číslom 4. - Zoskupovanie po 16 =4 x 4 hviezdičky. Po tomto kroku dostaneme:
1 veľkú skupinu, zostali 2 malé skupiny ... zvyšok 2 po delení čísla 6 číslom 4.
Záver:
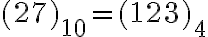 .
.
Posledný zápis hovorí, že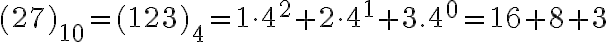 .
.
- zostali tri voľné (nezoskupené) hviezdičky ... 3
- dve menšie podmnožiny ... 2
- jedna veľká skupina ... 1
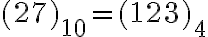 .
.
Posledný zápis hovorí, že
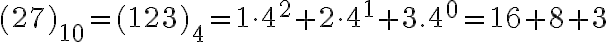 .
.
Postupné zoskupovanie, ktoré je znázornené na obrázku môžeme zapísať postupne ako delenie (so zvyškom) číslom 4.
Potom už stačí napísať získané zvyšky v poradí ako idú zdola nahor (a dopísať index 4). Pozrite si Excel súbor Tu
27 = 4.6 + 3
6 = 4.1 + 2
1 = 4.0 + 1
6 = 4.1 + 2
1 = 4.0 + 1
Veta o rozvoji prirodzeného čísla
Nech 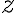 je prirodzené číslo,
je prirodzené číslo, 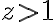 . Potom každé nenulové prirodzené číslo
. Potom každé nenulové prirodzené číslo  je možné jednoznačne vyjadriť v tvare:
je možné jednoznačne vyjadriť v tvare:
(R)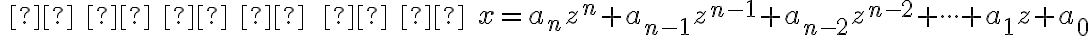 ,
,
kde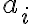 sú prirodzené čísla, pre ktoré platí
sú prirodzené čísla, pre ktoré platí 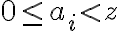 , pre
, pre 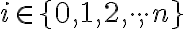 a
a 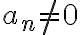 .
.
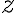 je prirodzené číslo,
je prirodzené číslo, 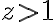 . Potom každé nenulové prirodzené číslo
. Potom každé nenulové prirodzené číslo  je možné jednoznačne vyjadriť v tvare:
je možné jednoznačne vyjadriť v tvare:(R)
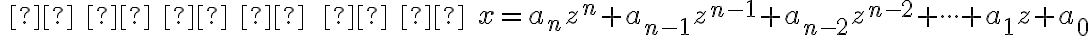 ,
,kde
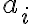 sú prirodzené čísla, pre ktoré platí
sú prirodzené čísla, pre ktoré platí 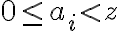 , pre
, pre 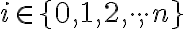 a
a 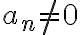 .
.
Ak je prirodzené číslo  zapísané v tvare (R) hovoríme, že sme ho vyjadrili v číselnej sústave o základe
zapísané v tvare (R) hovoríme, že sme ho vyjadrili v číselnej sústave o základe 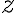 alebo v
alebo v 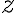 -adickej sústave. Skrátene píšeme
-adickej sústave. Skrátene píšeme
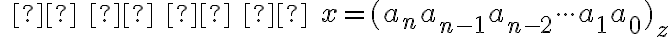 .
.
Pri zápise konkrétneho čísla môžeme zátvorky v predchádzajúcom zápise vynechať.
 zapísané v tvare (R) hovoríme, že sme ho vyjadrili v číselnej sústave o základe
zapísané v tvare (R) hovoríme, že sme ho vyjadrili v číselnej sústave o základe 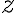 alebo v
alebo v 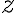 -adickej sústave. Skrátene píšeme
-adickej sústave. Skrátene píšeme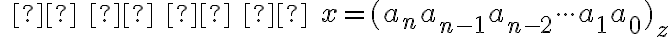 .
.Pri zápise konkrétneho čísla môžeme zátvorky v predchádzajúcom zápise vynechať.
Zápis čísla v sústave
Zapíšte číslo 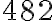 v číselnej sústave o základe
v číselnej sústave o základe 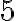
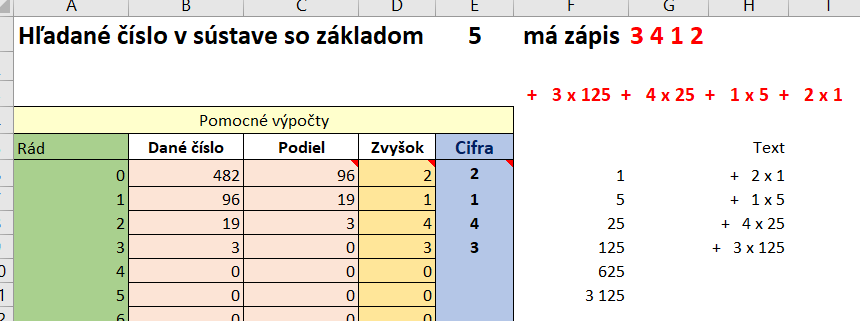
Postupným delením čísla 482 a následných čiastočných podielov číslom 5 postupne dostávame.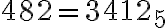 .
.
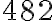 v číselnej sústave o základe
v číselnej sústave o základe 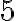
Postupným delením čísla 482 a následných čiastočných podielov číslom 5 postupne dostávame.
482 = 5 . 96 + 2
96 = 5 . 19 + 1
19 = 5 . 3 + 4
3 = 5 . 0 + 3
96 = 5 . 19 + 1
19 = 5 . 3 + 4
3 = 5 . 0 + 3
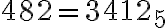 .
.  Otvor súbor EXCEL Tu
Otvor súbor EXCEL Tu
Ak chceme vyjadrovať čísla napríklad v sústave o základe 12, musíme mať k dispozícii 12 číslic.
Dohodneme sa, že číslo 10 označíme číslicou (symbolom) A a číslo 11 označíme číslicou (symbolom) B. Pri vyššom základe ako 12 postupujeme analogicky a využívame ďalšie písmená (C, D, E, ...).
Teraz môžeme riešiť aj nasledujúci príklad.
Dohodneme sa, že číslo 10 označíme číslicou (symbolom) A a číslo 11 označíme číslicou (symbolom) B. Pri vyššom základe ako 12 postupujeme analogicky a využívame ďalšie písmená (C, D, E, ...).
Teraz môžeme riešiť aj nasledujúci príklad.
Zapíšte číslo 279 v číselnej sústave o základe 12
Postupným delením čísla 279 a následných čiastočných podielov číslom 12 postupne dostávame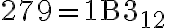 .
.
Postupným delením čísla 279 a následných čiastočných podielov číslom 12 postupne dostávame
279 = 12 . 23 + 3
23 = 12 . 1 + 11 (B)
1 = 12 . 0 + 1
23 = 12 . 1 + 11 (B)
1 = 12 . 0 + 1
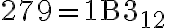 .
.
Preveďte číslo 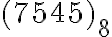 v číselnej sústave o základe
v číselnej sústave o základe 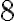 do číselnej sústavy so základom
do číselnej sústavy so základom 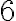 .
.
Pozrite si Excel súbor Tu
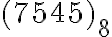 v číselnej sústave o základe
v číselnej sústave o základe 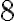 do číselnej sústavy so základom
do číselnej sústavy so základom 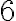 .
. Pozrite si Excel súbor Tu
Počtové výkony
Počtové výkony s prirodzenými číslami - sčítanie, násobenie
Pri sčitovaní v číselných sústavách o základe 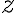 využívame dva spôsoby: spamäti a písomný. Žiaci poznajú algoritmy pre sčítanie resp. násobenie viacciferných čísel v desiatkovej sústave už zo základnej školy.
využívame dva spôsoby: spamäti a písomný. Žiaci poznajú algoritmy pre sčítanie resp. násobenie viacciferných čísel v desiatkovej sústave už zo základnej školy.
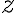 využívame dva spôsoby: spamäti a písomný. Žiaci poznajú algoritmy pre sčítanie resp. násobenie viacciferných čísel v desiatkovej sústave už zo základnej školy.
využívame dva spôsoby: spamäti a písomný. Žiaci poznajú algoritmy pre sčítanie resp. násobenie viacciferných čísel v desiatkovej sústave už zo základnej školy.Príklad. Vypočítajte v sedmičkovej sústave s využitím algoritmu pre písomné sčítanie: 263 + 324
Riešenie
|
263
+ 324
620 |
4 + 3 = 7 + 0
1 + 2 + 6 = 7 + 2 1 + 3 + 2 = 6 |
Príklad. Vypočítajte v sedmičkovej sústave s využitím algoritmu pre písomné násobenie: 63 x 3
Riešenie
|
63
x 3 252 |
3 x 3 = 7 + 2
1 + (3 x 6) = 2 x 7 + 5 2 + (3 x 0) = 2 |
Komentár k sčítaniu
• postup spočíva v tom, že najprv sčítame číslice rádu 0 4 + 3 = 7 + 0
• napíšeme číslicu 0 hľadaného súčtu a číslicu 1 pripočítame k súčtu číslic rádu 1 1 + 2 + 6 = 7 + 2
• napíšeme číslicu 2 a číslicu 1 pripočítame k súčtu číslic rádu 2 1 + 3 + 2 = 6
• napíšeme číslicu 6 pod daný rád
• napíšeme číslicu 0 hľadaného súčtu a číslicu 1 pripočítame k súčtu číslic rádu 1 1 + 2 + 6 = 7 + 2
• napíšeme číslicu 2 a číslicu 1 pripočítame k súčtu číslic rádu 2 1 + 3 + 2 = 6
• napíšeme číslicu 6 pod daný rád
Analogicky môžeme postupovať v číselnej sústave s ľubovoľným základom. Užitočné je mať napísanú tzv. tabuľku základných spojov pre sčítanie resp. násobenie pre danú sústavu. Vytvorte si takéto tabuľky pre číselnú sústavu so základom 9.
Vypočítajte v číselnej sústave so základom 9 ďalšie príklady vhodné pre žiakov SŠ.
Písomné delenie
Počtové výkony s prirodzenými číslami - delenie
Pri delení v číselných sústavách o základe 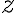 využívame prevažne len písomný algoritmus. Žiaci poznajú písomný algoritmus pre delenie viacciferných čísel v desiatkovej sústave zo základnej školy.
využívame prevažne len písomný algoritmus. Žiaci poznajú písomný algoritmus pre delenie viacciferných čísel v desiatkovej sústave zo základnej školy.
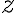 využívame prevažne len písomný algoritmus. Žiaci poznajú písomný algoritmus pre delenie viacciferných čísel v desiatkovej sústave zo základnej školy.
využívame prevažne len písomný algoritmus. Žiaci poznajú písomný algoritmus pre delenie viacciferných čísel v desiatkovej sústave zo základnej školy.
Príklad. Vypočítajte v osmičkovej sústave podiel: 413208
: 5. Použite algoritmus pre písomné delenie.
Riešenie
Pri riešení budeme potrebovať násobky čísla 5 osmičkovej číselnej sústave.
So žiakmi si najskôr vytvoríme takúto tabuľku („malú násobilku pre číslo 5“).
|
413208 : 5 = 65348
- 36
33
- 31 22 - 17 30 - 24 4 |
Odpoveď: Pri delení čísla 413208
číslom 5 je teda čiastočný podiel 65348 a zvyšok je 4.
Vypočítajte v číselnej sústave so základom 9 ďalšie príklady vhodné pre žiakov SŠ.
Kritériá (znaky) deliteľnosti
Medzi základné pojmy v aritmetike celých čísel patrí pojem deliteľnosti prirodzených (ale aj celých) čísel. Mnohé z vlastností deliteľnosti sú využiteľné aj v rôznych oblastiach matematiky. Vetu o delení so zvyškom využívajú žiaci už od ZŠ.
Veta o delení so zvyškom
Ku každým dvom prirodzeným číslam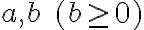 , existuje jediná dvojica celých čísel
, existuje jediná dvojica celých čísel 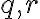 , pre ktorú platí:
, pre ktorú platí:
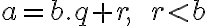 .
.
Číslo nazývame delenec, číslo
nazývame delenec, číslo  deliteľ, číslo
deliteľ, číslo  čiastočný (alebo neúplný) podiel a číslo
čiastočný (alebo neúplný) podiel a číslo  zvyšok.
zvyšok.
Ku každým dvom prirodzeným číslam
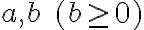 , existuje jediná dvojica celých čísel
, existuje jediná dvojica celých čísel 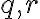 , pre ktorú platí:
, pre ktorú platí:
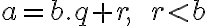 .
.
Číslo
 nazývame delenec, číslo
nazývame delenec, číslo  deliteľ, číslo
deliteľ, číslo  čiastočný (alebo neúplný) podiel a číslo
čiastočný (alebo neúplný) podiel a číslo  zvyšok.
zvyšok.
Pri delení prirodzeného čísla  nenulovým prirodzeným číslom
nenulovým prirodzeným číslom  dostaneme (čiastočný) podiel
dostaneme (čiastočný) podiel 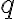 a zvyšok
a zvyšok 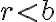 , pričom podiel a zvyšok sú delencom a deliteľom jednoznačne určené.
, pričom podiel a zvyšok sú delencom a deliteľom jednoznačne určené.
V nasledujúcom tvrdení zhrnieme niektoré zo základných vlastností deliteľnosti prirodzených čísel.
 nenulovým prirodzeným číslom
nenulovým prirodzeným číslom  dostaneme (čiastočný) podiel
dostaneme (čiastočný) podiel 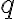 a zvyšok
a zvyšok 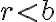 , pričom podiel a zvyšok sú delencom a deliteľom jednoznačne určené.
, pričom podiel a zvyšok sú delencom a deliteľom jednoznačne určené.V nasledujúcom tvrdení zhrnieme niektoré zo základných vlastností deliteľnosti prirodzených čísel.
Poznámka
Deliteľnosť 2, 5 a 10
Budeme sa venovať niektorým vybraným kritériám (znakom) deliteľnosti. Skúmajme, kedy je prirodzené číslo deliteľné dvomi.
Napíšme si niekoľko prirodzených čísel deliteľných dvomi: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30. Všimnime si ich posledné cifry. Vidíme, že na mieste jednotiek sa striedajú iba číslice 0, 2, 4, 6, 8.
Toto pozorovanie ľahko zovšeobecníme pre ľubovoľné prirodzené číslo.
Napíšme si niekoľko prirodzených čísel deliteľných dvomi: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30. Všimnime si ich posledné cifry. Vidíme, že na mieste jednotiek sa striedajú iba číslice 0, 2, 4, 6, 8.
Toto pozorovanie ľahko zovšeobecníme pre ľubovoľné prirodzené číslo.
Deliteľnosť dvomi
Nech číslo má rozvinutý zápis v desiatkovej číselnej sústave v tvare:
má rozvinutý zápis v desiatkovej číselnej sústave v tvare:
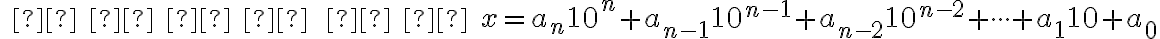
Skrátený zápis čísla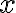 je v tvare
je v tvare
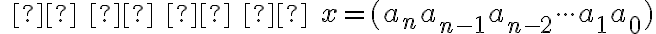
Nech číslo
 má rozvinutý zápis v desiatkovej číselnej sústave v tvare:
má rozvinutý zápis v desiatkovej číselnej sústave v tvare: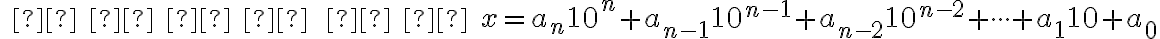
Skrátený zápis čísla
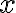 je v tvare
je v tvare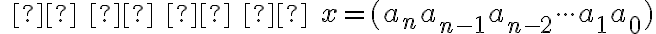
Rozvoj čísla 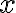 môžeme chápať aj ako súčet dvoch čísel:
môžeme chápať aj ako súčet dvoch čísel: 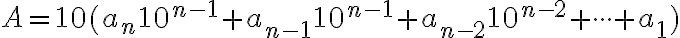 a čísla
a čísla 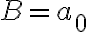 . Zrejme sčítanec
. Zrejme sčítanec 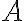 je deliteľný číslom 2. Deliteľnosť čísla
je deliteľný číslom 2. Deliteľnosť čísla  závisí len od toho, či aj druhý sčítanec, t.j. cifra nultého rádu
závisí len od toho, či aj druhý sčítanec, t.j. cifra nultého rádu 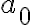 je párna. Súčasne vidíme, že od poslednej cifry závisí aj deliteľnosť číslom 5 a 10.
je párna. Súčasne vidíme, že od poslednej cifry závisí aj deliteľnosť číslom 5 a 10.
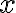 môžeme chápať aj ako súčet dvoch čísel:
môžeme chápať aj ako súčet dvoch čísel: 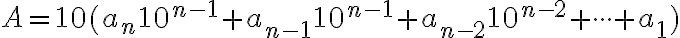 a čísla
a čísla 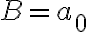 . Zrejme sčítanec
. Zrejme sčítanec 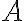 je deliteľný číslom 2. Deliteľnosť čísla
je deliteľný číslom 2. Deliteľnosť čísla  závisí len od toho, či aj druhý sčítanec, t.j. cifra nultého rádu
závisí len od toho, či aj druhý sčítanec, t.j. cifra nultého rádu 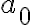 je párna. Súčasne vidíme, že od poslednej cifry závisí aj deliteľnosť číslom 5 a 10.
je párna. Súčasne vidíme, že od poslednej cifry závisí aj deliteľnosť číslom 5 a 10.
Tvrdenia, ktoré umožnia zistiť, či nejaké číslo je deliteľné iným (obvykle jednociferným) bez toho, aby sme vykonali delenie jedného druhým, sa volajú kritériá alebo znaky deliteľnosti.
Pre číselnú sústavu so základom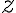 plat:
plat:
Pre číselnú sústavu so základom
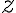 plat:
plat: Deliteľnosť 7
Zistite, či číslo 4851 je deliteľné 7?
485(1 * 2)
485 - (1 * 2) = 483
48 - (3 * 2) = 42
42 ... je deliteľné 7, preto je deliteľné aj pôvodné číslo.