Zhodnostné a podobnostné zobrazenia
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Zhodnostné a podobnostné zobrazenia |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 13:24 |
Zhodnostné zobrazenia
Analytické vyjadrenia zhodnostných zobrazení
Geometrické resp. konštrukčné vlastnosti zhodnostných zobrazení nájdete
Tu.
Definícia
Zobrazenie v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body
v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body 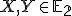 a ich obrazy
a ich obrazy 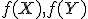 platí
platí
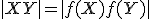 .
.
Inými slovami zhodné zobrazenia zachovávajú vzdialenosti bodov.
Zobrazenie
 v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body
v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body 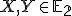 a ich obrazy
a ich obrazy 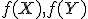 platí
platí
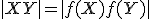 .
.
Inými slovami zhodné zobrazenia zachovávajú vzdialenosti bodov.
Dôkaz
Treba dokázať, že zhodnostné zobrazenie spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech
spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech 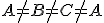 sú kolineárne body
sú kolineárne body 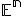 , potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov
, potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov 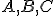 platí
platí 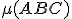 . Bod
. Bod 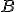 leží medzi bodmi
leží medzi bodmi 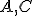 .
.
Ukážeme, že body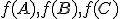 sú kolineárne a zároveň platí
sú kolineárne a zároveň platí 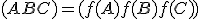 .
.
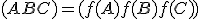 . Načrtnite si obrázok.
. Načrtnite si obrázok.
Treba dokázať, že zhodnostné zobrazenie
 spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech
spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech 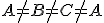 sú kolineárne body
sú kolineárne body 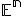 , potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov
, potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov 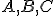 platí
platí 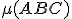 . Bod
. Bod 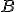 leží medzi bodmi
leží medzi bodmi 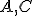 .
.
Ukážeme, že body
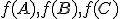 sú kolineárne a zároveň platí
sú kolineárne a zároveň platí 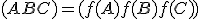 .
.
- Prvú časť tvrdenia dokážeme sporom. Nech body
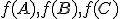 nie sú kolineárne, potom vytvárajú trojuholník a
na základe trojuholníkovej nerovnosti dostaneme spor.
nie sú kolineárne, potom vytvárajú trojuholník a
na základe trojuholníkovej nerovnosti dostaneme spor. - Teda body
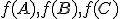 ležia na jednej priamke. Pre ich usporiadanie môžu nastať dva prípady, z ktorých iba prípad, keď bod
ležia na jednej priamke. Pre ich usporiadanie môžu nastať dva prípady, z ktorých iba prípad, keď bod 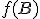 leží medzi bodmi
leží medzi bodmi 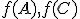 vyhovuje podmienkam:
vyhovuje podmienkam:
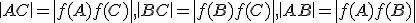 .
.
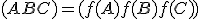 . Načrtnite si obrázok.
. Načrtnite si obrázok.
Osová súmernosť je oproti ostatným zhodným zobrazeniam niečím výnimočná. Má jednu veľmi zaujímavú vlastnosť, skladaním osových súmerností sa dajú získať
všetky zhodné zobrazenia v rovine. Z toho dôvodu začneme analytickým vyjadrením osovej súmernosti.
Geometrická interpretácia osovej súmernosti ako afinnej transformácie: Odvodenie rovníc Tu, Verzia "Repér" Tu

Geometrická interpretácia osovej súmernosti ako afinnej transformácie: Odvodenie rovníc Tu, Verzia "Repér" Tu
Posunutie
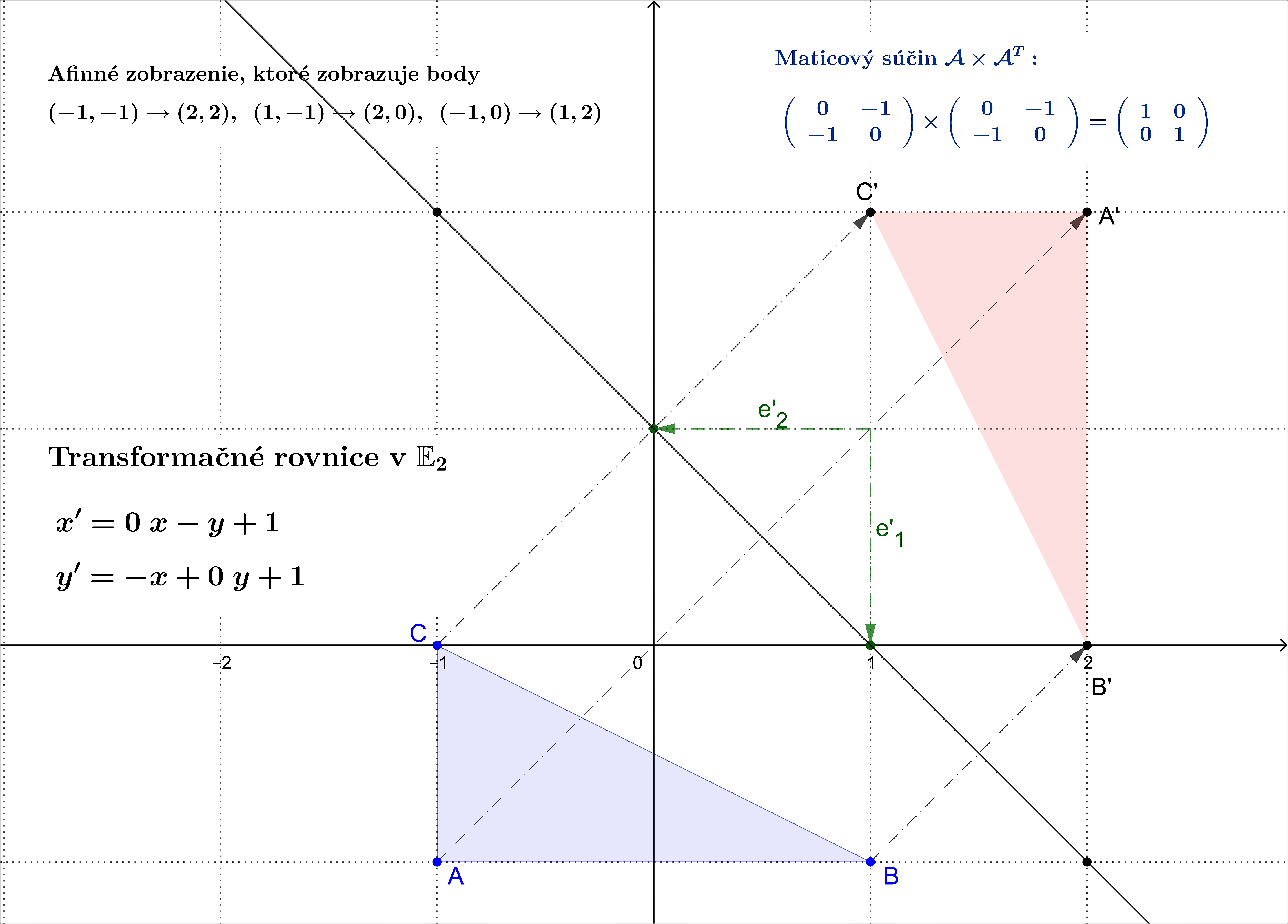
Posunutie je afinné zobrazenie určené vektorom posunutia 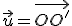 , kde
, kde ![\small O'=[p,q], \vec u =(p,q) \small O'=[p,q], \vec u =(p,q)](https://lms.umb.sk/filter/tex/pix.php/935a5f780f2084c71e7899ad6977cd4f.png) .
Posunutie je analyticky určené rovnicou
.
Posunutie je analyticky určené rovnicou
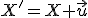
a prepísaním do maticového tvaru
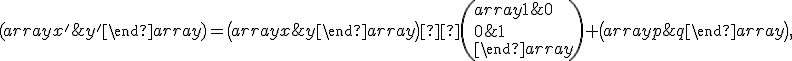 (1)
(1)
čo predstavuje transformačné rovnice
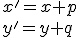 .
.
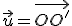 , kde
, kde ![\small O'=[p,q], \vec u =(p,q) \small O'=[p,q], \vec u =(p,q)](https://lms.umb.sk/filter/tex/pix.php/935a5f780f2084c71e7899ad6977cd4f.png) .
Posunutie je analyticky určené rovnicou
.
Posunutie je analyticky určené rovnicou
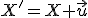
a prepísaním do maticového tvaru
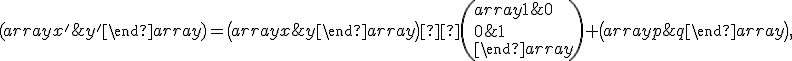 (1)
(1)
čo predstavuje transformačné rovnice
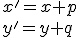 .
.
Tvrdenie
Posunutie v rovine je afinné zobrazenie a zároveň je zhodnostné. Dokážte to.
Posunutie v rovine je afinné zobrazenie a zároveň je zhodnostné. Dokážte to.
Riešenie
Poznáme obraz počiatku súradnej sústavy:![\small O' = [1,2] \small O' = [1,2]](https://lms.umb.sk/filter/tex/pix.php/10dcc2e27b46ae55829443bf31127cf3.png) a dosadením do vzťahu (1) dostaneme rovnice
a dosadením do vzťahu (1) dostaneme rovnice
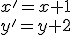 .
.
Pomoc - otvorte si applet Tu.
Poznáme obraz počiatku súradnej sústavy:
![\small O' = [1,2] \small O' = [1,2]](https://lms.umb.sk/filter/tex/pix.php/10dcc2e27b46ae55829443bf31127cf3.png) a dosadením do vzťahu (1) dostaneme rovnice
a dosadením do vzťahu (1) dostaneme rovnice
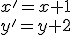 .
.
Pomoc - otvorte si applet Tu.
...
Osová súmernosť
Zhodnostné zobrazenie v rovine Osová súmernosť
Tri body
Osová súmernosť určená troma bodmi.
- Na určenie transformačných rovníc osovej súmernosti určenej osou súmernosti
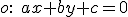 budeme potrebovať obrazy
troch rôznych bodov a ich obrazy v danej osovej súmernosti.
budeme potrebovať obrazy
troch rôznych bodov a ich obrazy v danej osovej súmernosti.
Najvýhodnejšie bude ak si zvolíme dva rôzne samodružné body a nejaký nesamodružný bod. Takými bodmi sú napríklad- dva body na osi súmernosti
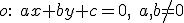 , pre ktoré platí
, pre ktoré platí ![\small A=[0,\frac{-c}{b}] \small A=[0,\frac{-c}{b}]](https://lms.umb.sk/filter/tex/pix.php/dd67a08dcc145362b583cb2c84e94ce1.png) a
a ![\small B=[\frac{-c}{a},0] \small B=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/b35dafcb91a2f8e7f3b1e89aeb667a55.png) ,
prípad ak jeden z koeficientov
,
prípad ak jeden z koeficientov 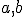 je rovný nule sa rieši zvlášť;
je rovný nule sa rieši zvlášť; - počiatok súradnej sústavy
![\small O=[0,0] \small O=[0,0]](https://lms.umb.sk/filter/tex/pix.php/b84d8e89cd0f49322ca9230458995576.png) , ktorého súradnice obrazu
, ktorého súradnice obrazu ![\small O'=[p,q] \small O'=[p,q]](https://lms.umb.sk/filter/tex/pix.php/7843bc3154f974357ba963a4d076a5bc.png) určíme pomocou "Matrix calculator":
určíme pomocou "Matrix calculator":
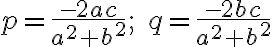 .
.
- dva body na osi súmernosti
- Potom dosadíme súradnice obrazov
![\small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0] \small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/15877e5bc55d5ebc24734962c92c4b49.png) do vzťahov
do vzťahov
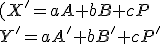
pričom musí platiť
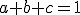 .
.
využitím Matrix calculator dostaneme riešenie
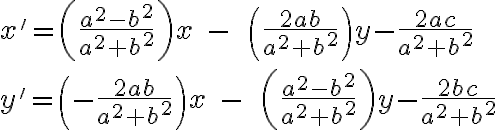
Repér
Osová súmernosť určená repérom.
Na určenie transformačných rovníc osovej súmernosti určenej osou súmernosti 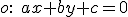 budeme potrebovať obraz súradného repéra
budeme potrebovať obraz súradného repéra
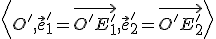
Postupne nájdeme:
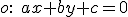 budeme potrebovať obraz súradného repéra
budeme potrebovať obraz súradného repéra
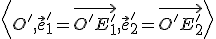
Postupne nájdeme:
- Obraz počiatku súradnej sústavy
![\small O'=[p,q] \small O'=[p,q]](https://lms.umb.sk/filter/tex/pix.php/9b214e8052bd6e14c00d9869d21efbbe.png) , ktorý určíme ako bod súmerný k bodu
, ktorý určíme ako bod súmerný k bodu ![\small O=[0,0] \small O=[0,0]](https://lms.umb.sk/filter/tex/pix.php/8b8044e750d6bcc556aaf5ed8f4fce4a.png) . Ten určíme pomocou priesečníka
. Ten určíme pomocou priesečníka 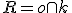 priamky
priamky 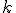 kolmej na priamku
kolmej na priamku  , ktorá prechádza bodom
, ktorá prechádza bodom 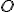 . Najskôr určíme
. Najskôr určíme
- Na určenie transformačných rovníc potrebujeme ešte aspoň dva rôzne body a ich obrazy v danej osovej súmernosti. Najvýhodnejšie bude ak si zvolíme dva samodružné body.
Takými bodmi sú ľubovoľné dva body na osi súmernosti
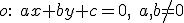 .
. - Zvoľme si
![\small A=[0,\frac{-c}{b}] \small A=[0,\frac{-c}{b}]](https://lms.umb.sk/filter/tex/pix.php/dd67a08dcc145362b583cb2c84e94ce1.png) a
a ![\small B=[\frac{-c}{a},0] \small B=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/b35dafcb91a2f8e7f3b1e89aeb667a55.png) , prípad ak jeden z koeficientov
, prípad ak jeden z koeficientov 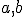 je rovný nule sa rieši zvlášť.
je rovný nule sa rieši zvlášť. - Potom dosadíme súradnice obrazov
![\small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0] \small O'=[p,q],A'=[0,\frac{-c}{b}],B'=[\frac{-c}{a},0]](https://lms.umb.sk/filter/tex/pix.php/15877e5bc55d5ebc24734962c92c4b49.png) do vzťahu
do vzťahu
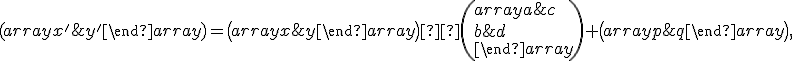 (1)
(1)
a dostaneme 4 rovnice o 4 neznámych
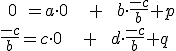
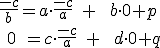
...
Otáčanie
Otáčanie je afinné zobrazenie určené stredom otáčania a uhlom otáčania. Analytické vyjadrenie má maticový tvar
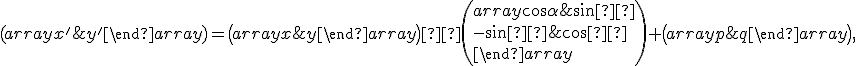 (2)
(2)
kde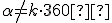 je uhol otočenia a
je uhol otočenia a 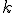 je celé číslo. Napríklad otočenie o orientovaný uhol
je celé číslo. Napríklad otočenie o orientovaný uhol 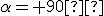 okolo
počiatku má analytický predpis
okolo
počiatku má analytický predpis
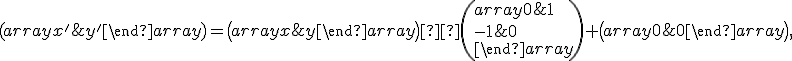
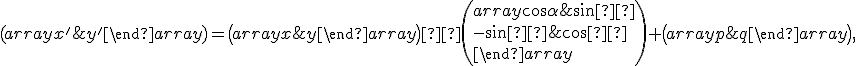 (2)
(2)
kde
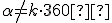 je uhol otočenia a
je uhol otočenia a 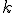 je celé číslo. Napríklad otočenie o orientovaný uhol
je celé číslo. Napríklad otočenie o orientovaný uhol 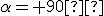 okolo
počiatku má analytický predpis
okolo
počiatku má analytický predpis
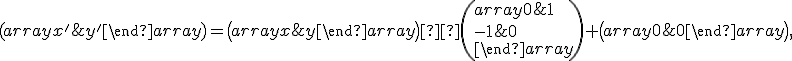
Tvrdenie
Otočenie v rovine je afinné zobrazenie a zároveň je zhodnostné. Dokážte to.
Otočenie v rovine je afinné zobrazenie a zároveň je zhodnostné. Dokážte to.
Príklad
V rovine je otočenie určené stredom![\small S = [−1; 1] \small S = [−1; 1]](https://lms.umb.sk/filter/tex/pix.php/29133975b65446dd0b21e48795ced112.png) a o orientovaným uhlom
a o orientovaným uhlom 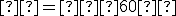 . Určite jeho transformačné rovnice a obraz kružnice
. Určite jeho transformačné rovnice a obraz kružnice
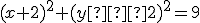 .
.
V rovine je otočenie určené stredom
![\small S = [−1; 1] \small S = [−1; 1]](https://lms.umb.sk/filter/tex/pix.php/29133975b65446dd0b21e48795ced112.png) a o orientovaným uhlom
a o orientovaným uhlom 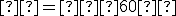 . Určite jeho transformačné rovnice a obraz kružnice
. Určite jeho transformačné rovnice a obraz kružnice
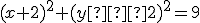 .
.
Riešenie
Musíme určiť obraz počiatku súradnej sústavy. Súradnice bodu![\small O' = [p,q] \small O' = [p,q]](https://lms.umb.sk/filter/tex/pix.php/6e3ae7aa8eed85755323e42a70d98402.png) dosadíme do vzťahu (2 dostaneme rovnice
dosadíme do vzťahu (2 dostaneme rovnice
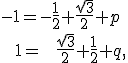
pričom využijeme skutočnosť poznáme vzor a obraz stredu![\small S = [−1; 1] \small S = [−1; 1]](https://lms.umb.sk/filter/tex/pix.php/29133975b65446dd0b21e48795ced112.png) , ktorý je samodružný.
, ktorý je samodružný.
Riešením je bod![\small O' = [\frac{-1-\sqrt{3}}{2}; \frac{1-\sqrt{3}}{2}] \small O' = [\frac{-1-\sqrt{3}}{2}; \frac{1-\sqrt{3}}{2}]](https://lms.umb.sk/filter/tex/pix.php/9ab3384edd44c065d24163885cb44633.png) .
.
Obraz kružnice určíme tak, že vypočítame súradnice obrazu stredu kružnice dosadením![\small S = [−1; 1] \small S = [−1; 1]](https://lms.umb.sk/filter/tex/pix.php/29133975b65446dd0b21e48795ced112.png) do transformačných rovníc. Polomer kružnice sa v zhodnom zobrazení nemení a bude rovný
do transformačných rovníc. Polomer kružnice sa v zhodnom zobrazení nemení a bude rovný  . Zostrojte obraz kružnice v GeoGebre pomocou nástroja "Množina bodov" v applete Tu.
. Zostrojte obraz kružnice v GeoGebre pomocou nástroja "Množina bodov" v applete Tu.
Musíme určiť obraz počiatku súradnej sústavy. Súradnice bodu
![\small O' = [p,q] \small O' = [p,q]](https://lms.umb.sk/filter/tex/pix.php/6e3ae7aa8eed85755323e42a70d98402.png) dosadíme do vzťahu (2 dostaneme rovnice
dosadíme do vzťahu (2 dostaneme rovnice
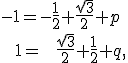
pričom využijeme skutočnosť poznáme vzor a obraz stredu
![\small S = [−1; 1] \small S = [−1; 1]](https://lms.umb.sk/filter/tex/pix.php/29133975b65446dd0b21e48795ced112.png) , ktorý je samodružný.
, ktorý je samodružný.
Riešením je bod
![\small O' = [\frac{-1-\sqrt{3}}{2}; \frac{1-\sqrt{3}}{2}] \small O' = [\frac{-1-\sqrt{3}}{2}; \frac{1-\sqrt{3}}{2}]](https://lms.umb.sk/filter/tex/pix.php/9ab3384edd44c065d24163885cb44633.png) .
.
Obraz kružnice určíme tak, že vypočítame súradnice obrazu stredu kružnice dosadením
![\small S = [−1; 1] \small S = [−1; 1]](https://lms.umb.sk/filter/tex/pix.php/29133975b65446dd0b21e48795ced112.png) do transformačných rovníc. Polomer kružnice sa v zhodnom zobrazení nemení a bude rovný
do transformačných rovníc. Polomer kružnice sa v zhodnom zobrazení nemení a bude rovný  . Zostrojte obraz kružnice v GeoGebre pomocou nástroja "Množina bodov" v applete Tu.
. Zostrojte obraz kružnice v GeoGebre pomocou nástroja "Množina bodov" v applete Tu....
Príklady a cvičenie
Riešenie
Keďže máme obraz repéra, tak môžeme použiť geometrický model "Obraz repéru" Tu, v ktorom nastavíme odpovedajúce hodnoty pre obraz repéra.
Repér pre dané afinné zobrazenie je![\small O'=[1, 1], \overrightarrow{e'_1}=(0, -1 , \overrightarrow{e'_2}=(-1, 0) \rbrace \small O'=[1, 1], \overrightarrow{e'_1}=(0, -1 , \overrightarrow{e'_2}=(-1, 0) \rbrace](https://lms.umb.sk/filter/tex/pix.php/04f483745713111a02c837bbd052ec8a.png) .
Transformačné rovnice budú mať analytické vyjadrenie
.
Transformačné rovnice budú mať analytické vyjadrenie
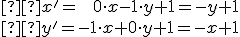
Skúmajme, či táto transformácia má samodružné body. Ak bod![\small M=[x, y] \small M=[x, y]](https://lms.umb.sk/filter/tex/pix.php/afca5e5a17438cf3e0eb295dfb5c122d.png) je samodružný, tak musí pre jeho obraz
je samodružný, tak musí pre jeho obraz ![\small f(M)=M'[x', y'] \small f(M)=M'[x', y']](https://lms.umb.sk/filter/tex/pix.php/5d3cc6ed6b8ac44ffd056d25fdb2687d.png) platiť:
platiť:
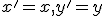 .
.
Po dosadení do transformačných rovníc dostaneme
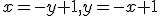 ,
,
čo je množina bodov = priamka. Neskôr ukážeme, že transformácia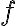 je zhodné zobrazenie.
Preto priamka samodružných bodov
je zhodné zobrazenie.
Preto priamka samodružných bodov 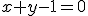 je osou súmernosti.
je osou súmernosti.
Geometrická interpretácia - riešenie Tu
Keďže máme obraz repéra, tak môžeme použiť geometrický model "Obraz repéru" Tu, v ktorom nastavíme odpovedajúce hodnoty pre obraz repéra.
Repér pre dané afinné zobrazenie je
![\small O'=[1, 1], \overrightarrow{e'_1}=(0, -1 , \overrightarrow{e'_2}=(-1, 0) \rbrace \small O'=[1, 1], \overrightarrow{e'_1}=(0, -1 , \overrightarrow{e'_2}=(-1, 0) \rbrace](https://lms.umb.sk/filter/tex/pix.php/04f483745713111a02c837bbd052ec8a.png) .
Transformačné rovnice budú mať analytické vyjadrenie
.
Transformačné rovnice budú mať analytické vyjadrenie
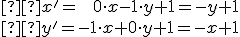
Skúmajme, či táto transformácia má samodružné body. Ak bod
![\small M=[x, y] \small M=[x, y]](https://lms.umb.sk/filter/tex/pix.php/afca5e5a17438cf3e0eb295dfb5c122d.png) je samodružný, tak musí pre jeho obraz
je samodružný, tak musí pre jeho obraz ![\small f(M)=M'[x', y'] \small f(M)=M'[x', y']](https://lms.umb.sk/filter/tex/pix.php/5d3cc6ed6b8ac44ffd056d25fdb2687d.png) platiť:
platiť:
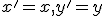 .
.
Po dosadení do transformačných rovníc dostaneme
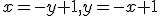 ,
,
čo je množina bodov = priamka. Neskôr ukážeme, že transformácia
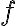 je zhodné zobrazenie.
Preto priamka samodružných bodov
je zhodné zobrazenie.
Preto priamka samodružných bodov 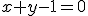 je osou súmernosti.
je osou súmernosti.
Geometrická interpretácia - riešenie Tu
Príklad 2
V rovine je posunutie určené vektorom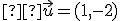 . V posunutí sa trojuholník
. V posunutí sa trojuholník 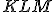 so súradnicami
so súradnicami ![\small K = [1; 1], L = [4; 3], M = [2; 5] \small K = [1; 1], L = [4; 3], M = [2; 5]](https://lms.umb.sk/filter/tex/pix.php/e3495d469cb175a5fccd8317021b70f7.png) zobrazí sa na
trojuholník
zobrazí sa na
trojuholník 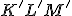 so súradnicami
so súradnicami ![\small K'= [2; -1], L' = [5; 1], M' = [3; 3] \small K'= [2; -1], L' = [5; 1], M' = [3; 3]](https://lms.umb.sk/filter/tex/pix.php/fcd9c282160c70ca989a499b862178aa.png) .
.
a) Narysujte obraz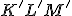 v GeoGebre pomocou nástroja Posunutie.
v GeoGebre pomocou nástroja Posunutie.
b) Nájdite analytické vyjadrenie tejto zhodnosti.
Návod: Poznáme obrazy![\small O'= [1; -2], K' = [2; -1], M' = [3; 3] \small O'= [1; -2], K' = [2; -1], M' = [3; 3]](https://lms.umb.sk/filter/tex/pix.php/9e85f67c85cfe23fd070431a6d8fa740.png) a ich dosadením spolu so súradnicami
a ich dosadením spolu so súradnicami ![\small K = [1; 1], M = [2; 5] \small K = [1; 1], M = [2; 5]](https://lms.umb.sk/filter/tex/pix.php/de2eabc53d5450b1d9bdb6a8e232f2be.png) do rovnice
do rovnice
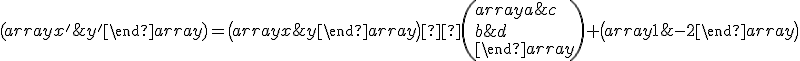
dostaneme 4 rovnice o 4 neznámych
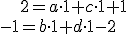
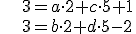
Riešenie sústavy v GeoGebre Tu . Pomoc - otvorte si applet Tu.
V rovine je posunutie určené vektorom
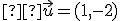 . V posunutí sa trojuholník
. V posunutí sa trojuholník 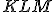 so súradnicami
so súradnicami ![\small K = [1; 1], L = [4; 3], M = [2; 5] \small K = [1; 1], L = [4; 3], M = [2; 5]](https://lms.umb.sk/filter/tex/pix.php/e3495d469cb175a5fccd8317021b70f7.png) zobrazí sa na
trojuholník
zobrazí sa na
trojuholník 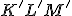 so súradnicami
so súradnicami ![\small K'= [2; -1], L' = [5; 1], M' = [3; 3] \small K'= [2; -1], L' = [5; 1], M' = [3; 3]](https://lms.umb.sk/filter/tex/pix.php/fcd9c282160c70ca989a499b862178aa.png) .
.
a) Narysujte obraz
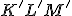 v GeoGebre pomocou nástroja Posunutie.
v GeoGebre pomocou nástroja Posunutie.
b) Nájdite analytické vyjadrenie tejto zhodnosti.
Návod: Poznáme obrazy
![\small O'= [1; -2], K' = [2; -1], M' = [3; 3] \small O'= [1; -2], K' = [2; -1], M' = [3; 3]](https://lms.umb.sk/filter/tex/pix.php/9e85f67c85cfe23fd070431a6d8fa740.png) a ich dosadením spolu so súradnicami
a ich dosadením spolu so súradnicami ![\small K = [1; 1], M = [2; 5] \small K = [1; 1], M = [2; 5]](https://lms.umb.sk/filter/tex/pix.php/de2eabc53d5450b1d9bdb6a8e232f2be.png) do rovnice
do rovnice
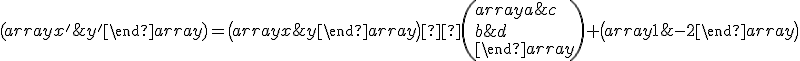
dostaneme 4 rovnice o 4 neznámych
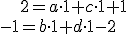
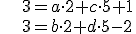
Riešenie sústavy v GeoGebre Tu . Pomoc - otvorte si applet Tu.
Príklad 3
Je daná osová súmernosť osou , ktorá je určená bodmi
, ktorá je určená bodmi ![\small Q_1 = [-2; -3], Q_2 = [4; 3] \small Q_1 = [-2; -3], Q_2 = [4; 3]](https://lms.umb.sk/filter/tex/pix.php/356732ad02ffeb1c057449896fc9634d.png) a štvoruholník
a štvoruholník 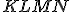 .
.
a) Narysujte obraz štvoruholníka obraz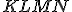 v GeoGebre pomocou nástroja Osová súmernosť.
v GeoGebre pomocou nástroja Osová súmernosť.
Štvoruholník zvoľte tak, aby jeho dve strany pretínali os súmernosti.
b) Určte analytické vyjadrenie osovej súmernosti. Návod analogický ako v predchádzajúcej úlohe alebo zostrojte obrazy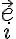 .
Matica transformácie pre osovú súmernosť Tu
.
Matica transformácie pre osovú súmernosť Tu
Je daná osová súmernosť osou
 , ktorá je určená bodmi
, ktorá je určená bodmi ![\small Q_1 = [-2; -3], Q_2 = [4; 3] \small Q_1 = [-2; -3], Q_2 = [4; 3]](https://lms.umb.sk/filter/tex/pix.php/356732ad02ffeb1c057449896fc9634d.png) a štvoruholník
a štvoruholník 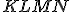 .
. a) Narysujte obraz štvoruholníka obraz
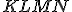 v GeoGebre pomocou nástroja Osová súmernosť.
v GeoGebre pomocou nástroja Osová súmernosť.
Štvoruholník zvoľte tak, aby jeho dve strany pretínali os súmernosti.
b) Určte analytické vyjadrenie osovej súmernosti. Návod analogický ako v predchádzajúcej úlohe alebo zostrojte obrazy
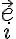 .
Matica transformácie pre osovú súmernosť Tu
.
Matica transformácie pre osovú súmernosť Tu
Cvičenie
- Riešte úlohy zo zbierky Monoszová - čast 4.3, 4.4. a 4.5.
- Zistite, či posunutie
 roviny
roviny 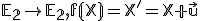 pre pevne zvolený
vektor posunutia
pre pevne zvolený
vektor posunutia 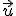 je afinné zobrazenie.
je afinné zobrazenie. - Určite obraz trojuholníka
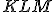 , kde
, kde ![\small K = [−3; 5], L = [−5; 2], M = [1; 3] \small K = [−3; 5], L = [−5; 2], M = [1; 3]](https://lms.umb.sk/filter/tex/pix.php/49ef7f12dbd3bf345b8b2efcf2e6701b.png) v stredovej súmernosti určené analytickým vyjadrením
v stredovej súmernosti určené analytickým vyjadrením
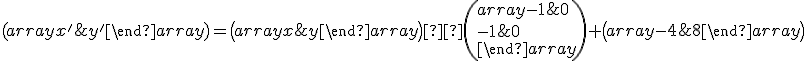 . Návod pozri v práci (Ptáčková, 2016, str.64), dostupné Tu.
. Návod pozri v práci (Ptáčková, 2016, str.64), dostupné Tu. - Riešte ďalšie úlohy z práce (Ptáčková, 2016, od str.65).
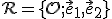
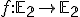
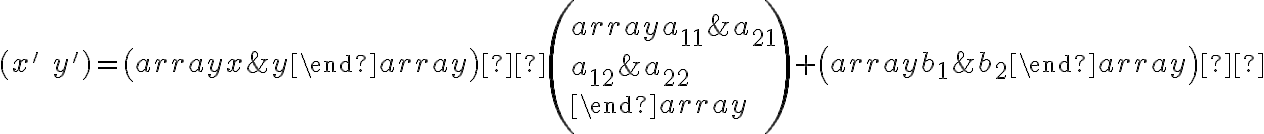
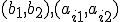
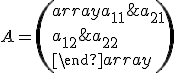
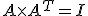
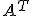
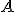
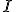

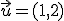

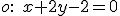
![\small O'=[\frac{4}{5},\frac{8}{5}],A'=[0,1],B'=[2,0] \small O'=[\frac{4}{5},\frac{8}{5}],A'=[0,1],B'=[2,0]](https://lms.umb.sk/filter/tex/pix.php/47a5a636b0a629e5cbc960ea12a787c6.png)
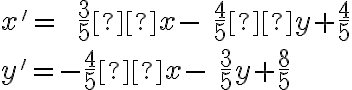
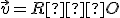
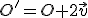
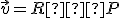
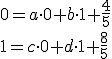
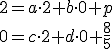
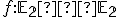
![\small O=[0, 0] \rightarrow O'=[1, 1] \small O=[0, 0] \rightarrow O'=[1, 1]](https://lms.umb.sk/filter/tex/pix.php/0765f044b47d3ef64bf5d8ac93a2a27b.png)
![\small \overrightarrow{e_1} =[1, 0] \rightarrow \overrightarrow{e'_1} =(0, -1) \small \overrightarrow{e_1} =[1, 0] \rightarrow \overrightarrow{e'_1} =(0, -1)](https://lms.umb.sk/filter/tex/pix.php/b99eb702a27fe10d9abc98f574ba3cda.png)
![\small \overrightarrow{e_2}=[0, 1] \rightarrow \overrightarrow{e'_2}=(-1, 0) \small \overrightarrow{e_2}=[0, 1] \rightarrow \overrightarrow{e'_2}=(-1, 0)](https://lms.umb.sk/filter/tex/pix.php/9fb07fc8c4a703075755f8eaf43dce94.png)