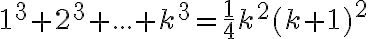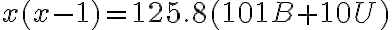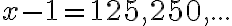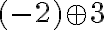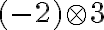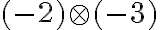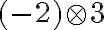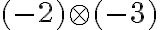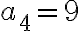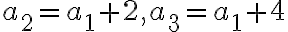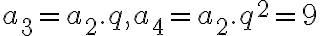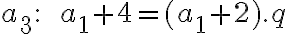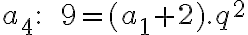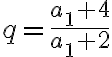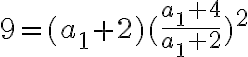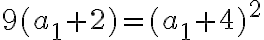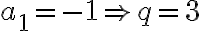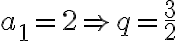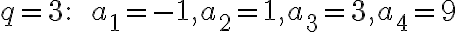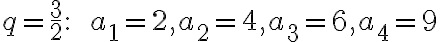RŠM - riešenia úloh
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | RŠM - riešenia úloh |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | sobota, 11 mája 2024, 12:08 |
Úvodné cvičenie
-
Pomocou matematickej indukcie dokážte, že pre všetky prirodzené čísla
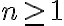 platí:
platí:
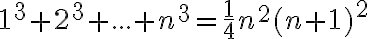
- Preveďte číslo (268)9 do dvanásťkovej číselnej sústavy.
- Doplňte miesto hviezdičiek číslice tak, aby výsledok bol správny: 8*06 – 78*8 = **8* .
-
Nájdite v desiatkovej číselnej sústave také trojciferné číslo
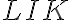 , aby platilo
, aby platilo 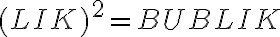 . Písmená
. Písmená 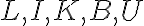 predstavujú cifry čísel.
predstavujú cifry čísel.
Úloha 2 a 3
Preveďte číslo (268)9 do dvanásťkovej číselnej sústavy.
Pozri súbor Excel Tu
Doplňte miesto hviezdičiek číslice tak, aby výsledok bol správny: 8*06 – 78*8 = **8*
Postupujeme sprava
platí, že posledná cifra na pravej strane rovnosti sa musí rovnať 8 lebo (16-8=8)
po dosadení máme: 8*06 - 78*8 = **88
tretia cifra v druhom čísle musí byť rovná 1 lebo (10-(1+1) = 8)
po dosadení: 8*06 - 7818 = **88 zistíme, že druhá cifra v čísle na pravej strane je rovná 0 lebo (9-(8+1) = 0)
podobnými úvahami prídeme k záveru: 8906 - 7818 = 1088
platí, že posledná cifra na pravej strane rovnosti sa musí rovnať 8 lebo (16-8=8)
po dosadení máme: 8*06 - 78*8 = **88
tretia cifra v druhom čísle musí byť rovná 1 lebo (10-(1+1) = 8)
po dosadení: 8*06 - 7818 = **88 zistíme, že druhá cifra v čísle na pravej strane je rovná 0 lebo (9-(8+1) = 0)
podobnými úvahami prídeme k záveru: 8906 - 7818 = 1088
Prirodzené čísla
-
Súčet
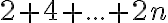 zapíšte pomocou sumačnej symboliky, nájdite vzorec (formulu) pre jeho výpočet a pomocou neho vypočítajte 50+52+...+200.
zapíšte pomocou sumačnej symboliky, nájdite vzorec (formulu) pre jeho výpočet a pomocou neho vypočítajte 50+52+...+200. - V dvojcifernom čísle je jedna číslica väčšia do druhej o 1. Súčet druhých mocnín tohto čísla a čísla napísaného tými istými číslicami v obrátenom poradí je 1 553. Určte takéto dvojciferné číslo.
- Pomocou peanových axióm spočítajte:
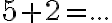
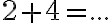
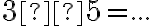
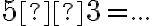
Úloha 1
Zápis 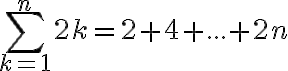
máme aritmetickú postupnosť, ktorej súčet prvých členov vypočítame pomocou vzorca
členov vypočítame pomocou vzorca
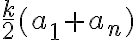 , kde
, kde 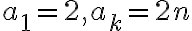
po dosadení týchto hodnôt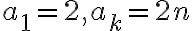 dostaneme
dostaneme
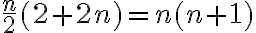 .
.
Vypočítať 50 + 52 +...+ 200 znamená najprv sčítať všetky párne čísla 2 + 4 +...+ 200 a potom odpočítať súčet 2 + 4 +...+ 48.
Súčet všetkých párnych čísel bude rovný
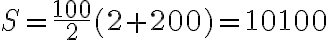
a súčet párnych čísel menších ako 50 je rovný
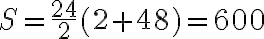 .
.
Rozdiel je rovný 9 500.
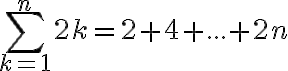
máme aritmetickú postupnosť, ktorej súčet prvých
 členov vypočítame pomocou vzorca
členov vypočítame pomocou vzorca
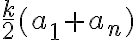 , kde
, kde 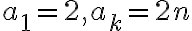
po dosadení týchto hodnôt
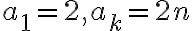 dostaneme
dostaneme
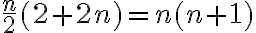 .
.
Vypočítať 50 + 52 +...+ 200 znamená najprv sčítať všetky párne čísla 2 + 4 +...+ 200 a potom odpočítať súčet 2 + 4 +...+ 48.
Súčet všetkých párnych čísel bude rovný
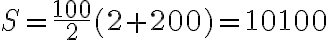
a súčet párnych čísel menších ako 50 je rovný
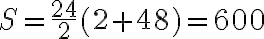 .
.
Rozdiel je rovný 9 500.
Úlohy 2 a 3
- Nech hľadané číslo
 má cifry
má cifry
 .
.
To znamená, že skrátený zápis v desiatkovej číselnej sústave má tvar
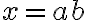
rozvinutý zápis v desiatkovej číselnej sústave má tvar
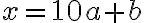 .
.
Číslo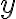 napísané tými istými číslicami v obrátenom poradí má rozvinutý tvar
napísané tými istými číslicami v obrátenom poradí má rozvinutý tvar
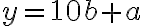 .
.
Podľa zadania musí platiť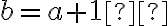 a zároveň
a zároveň 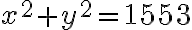 .
.
Po dosadení dostaneme rovnicu
![[10a+(a+1)]^2+[10(a+1)+a]^2=1553 [10a+(a+1)]^2+[10(a+1)+a]^2=1553](https://lms.umb.sk/filter/tex/pix.php/e66e450a61ca5f1728e4bb6fb0974440.png) resp.
resp. ![[121a^2+22a+1)]+[121a^2+220a+100]=1553 [121a^2+22a+1)]+[121a^2+220a+100]=1553](https://lms.umb.sk/filter/tex/pix.php/1022d7fbb020c7c4d9684a87eb9a57d5.png)
Po úprave dostaneme kvadratickú rovnicu
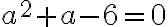 ,
,
ktorej riešením sú čísla -3, 2. Vyhovuje len kladná (cifra)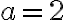 .
.
Hľadané číslo je 23. - Počítajme 5 + 2 = (5 + 1') = (5 + 1)'= (5 + 0')' = (5 + 0)'' = 5''= 6' = 7 . Počítajme 5 x 3 = (5 x 2') = 5 x 2 + 5 =... = 10 + 5=15
Celé čísla
- Spočítajte a zdôvodnite v obore celých čísel:
-
V množine celých čísel riešte rovnicu riešte nerovnicu
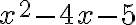
-
Čísla
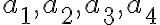 majú vlastnosť, že prvé tri sú po sebe idúce členy aritmetickej postupnosti s diferenciou
majú vlastnosť, že prvé tri sú po sebe idúce členy aritmetickej postupnosti s diferenciou 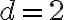 a posledné tri sú po sebe idúce členy geometrickej postupnosti. Určte
tieto čísla, ak platí
a posledné tri sú po sebe idúce členy geometrickej postupnosti. Určte
tieto čísla, ak platí 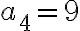 . Bušek. I.: Řešené maturitní úlohy z matematiky. Praha 1999.
. Bušek. I.: Řešené maturitní úlohy z matematiky. Praha 1999.
Úloha 1
-
Nech celé číslo
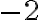 reprezentuje dvojica prirodzených čísel
reprezentuje dvojica prirodzených čísel 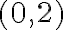 a nech číslo
a nech číslo 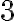 reprezentuje dvojica čísel
reprezentuje dvojica čísel 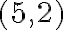 . Z definície súčtu
. Z definície súčtu 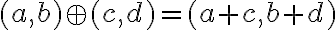 celých čísel dostaneme
celých čísel dostaneme
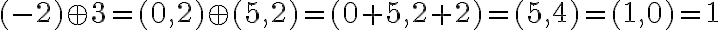 .
.
-
Podobne budeme postupovať pre "súčet
 " čísel
" čísel 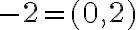 čísla
čísla 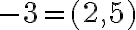
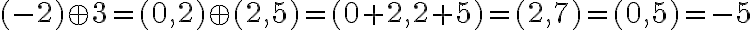 .
.
-
Pre "súčin
 " čísla
" čísla 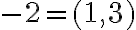 a čísla
a čísla 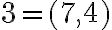 . Z definície súčinu
. Z definície súčinu 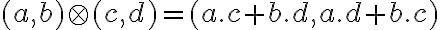 dostaneme
dostaneme
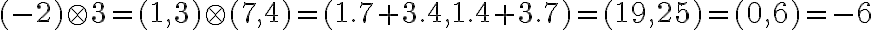 .
.
-
Podobne budeme postupovať pre "súčin
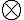 " čísel
" čísel 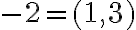 čísla
čísla 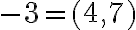 .
.

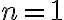
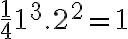
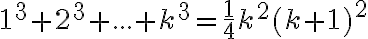
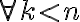
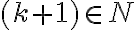
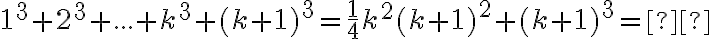
![=(k+1)^2(\frac{1}{4} k^2+ (k + 1) ] = \frac{1}{4}(k+1)^2(k^2+4k+4)=\frac{1}{4}(k+1)^2[(k+1)+1]^2 =(k+1)^2(\frac{1}{4} k^2+ (k + 1) ] = \frac{1}{4}(k+1)^2(k^2+4k+4)=\frac{1}{4}(k+1)^2[(k+1)+1]^2](https://lms.umb.sk/filter/tex/pix.php/99b105e23f7d087eb7a20298b9ae05aa.png)