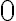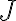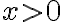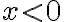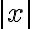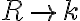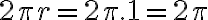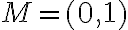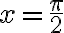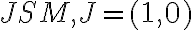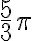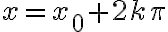Goniometrické funkcie
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Goniometrické funkcie |
| Vytlačil(a): | Gast |
| Dátum: | streda, 3 júla 2024, 11:40 |
Historické poznámky
Stručný prierez vývojom
- Už cca okolo roku 1900 pred n. l. starí babylonskí astronómovia zaznamenávali polohu a pohyby hviezd, pričom používali základy sférickej trigonometrie.
- Staroveký Babylončania - delenie plného uhla na 360 rovnakých dielov. Oblúková miera - 1 radián (Thomson v roku 1871) je stredový uhol, ktorý prislúcha oblúku s rovnakou dĺžkou, ako je polomer kružnice.
- Názov goniometria pochádza z gréčtiny: gónia - uhol, roh a metron - merať) - oblasť matematiky, ktorá sa zaoberá goniometrickými funkciami
- Staroveké Grécko (Thales a výška pyramídy, slnečné hodiny - tieň tyče a funkcia kotangens - pomer dĺžky stĺpa a dĺžky tieňa).
- Názov „trigonometria“ pochádza z gréčtiny a znamená „merať trojuholník“.
- Pojem goniometrické funkcie v preklade z gréčtiny znamená funkcie merajúce uhly.
- Astronóm Hipparchos (pochádzal z Nikaie v Bitýnii, obdobie asi 190 – 120 pred n. l.) a Klaudios Ptolemaios (asi 85 – 165 n. l.)
Pre trojuholník vpísaný do kruhu je každá strana tetivou kružnice. K výpočtu prvkov trojuholníka stačí určiť dĺžku tetivy pomocou stredového uhla, čo je dvojnásobný sínus polovice stredového uhla.
Hipparchos zostavil tabuľky tetív (sínusov) pre rôzne stredové uhly kružnice pri stálom polomere. Napísal dvanásť kníh k tejto problematike. Písomné doklady pochádzajú od Ptolemaios v knihe Almagest.[1]
Hipparchos zostavil tabuľky tetív (sínusov) pre rôzne stredové uhly kružnice pri stálom polomere. Napísal dvanásť kníh k tejto problematike. Písomné doklady pochádzajú od Ptolemaios v knihe Almagest.[1]
[1] Smýkalová, R. : Goniometrické funkce v elementární matematice. (Czech). Brno, 2016. Dostupné na: https://dml.cz/handle/10338.dmlcz/404316
Arabskí učenci zaviedli pojem sínus ako vzťah medzi polovicou uhla a polovicou tetivy.
Arddhadžíva (džíva) - dĺžka polovice tetivy. Arabský preklad: džiba 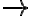 džaib (prsia, výstrih, vypuklosť). V 12. storočí preklad do latinčiny: sinus.
džaib (prsia, výstrih, vypuklosť). V 12. storočí preklad do latinčiny: sinus.
V 6. storočí Varahamihira vo svojej práci použil vzorec pre súčet kvadrátov sin a cos. Všetky spomínané trigonometrické veličiny skúmali Indovia iba v rozmedzí prvého kvadrantu, teda v uzavretom intervale .
.
Analytický pohľad na goniometrické funkcie vytvoril Leonhard Euler roku 1748 v spise Introductio in analysin infinitorum [2], kde tieto funkcie definoval pomocou nekonečných radov. Používal zápisy: sin., cos., tang., cot., sec., a cosec.
_________________________________________________________________________________________
[2] INTRODUCTIO IN ANALYSIN INFINITORUM. Translated and annotated by. Ian Bruce Dostupné na: http://www.17centurymaths.com/contents/introductiontoanalysisvol1.htm resp. Tu
text
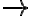 džaib (prsia, výstrih, vypuklosť). V 12. storočí preklad do latinčiny: sinus.
džaib (prsia, výstrih, vypuklosť). V 12. storočí preklad do latinčiny: sinus.
V 6. storočí Varahamihira vo svojej práci použil vzorec pre súčet kvadrátov sin a cos. Všetky spomínané trigonometrické veličiny skúmali Indovia iba v rozmedzí prvého kvadrantu, teda v uzavretom intervale
 .
.
Analytický pohľad na goniometrické funkcie vytvoril Leonhard Euler roku 1748 v spise Introductio in analysin infinitorum [2], kde tieto funkcie definoval pomocou nekonečných radov. Používal zápisy: sin., cos., tang., cot., sec., a cosec.
_________________________________________________________________________________________
[2] INTRODUCTIO IN ANALYSIN INFINITORUM. Translated and annotated by. Ian Bruce Dostupné na: http://www.17centurymaths.com/contents/introductiontoanalysisvol1.htm resp. Tu
Definície funkcií
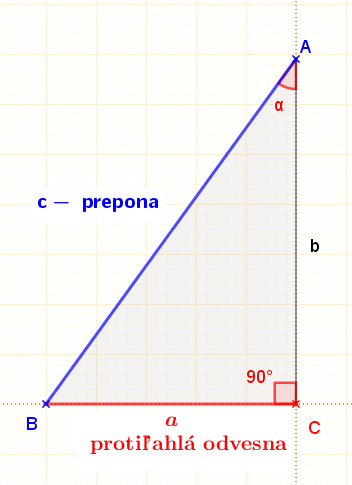
Sínus ostrého uhla v pravouhlom trojuholníku je pomer dĺžky protiľahlej odvesny ostrého uhla k dĺžke prepony.
Kosínus ostrého uhla v pravouhlom trojuholníku je pomer dĺžky priľahlej odvesny ostrého uhla k dĺžke prepony.
 applet
applet 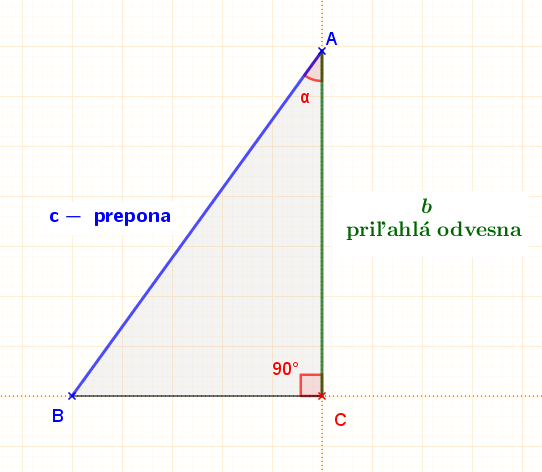 sin
sin 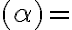 sin
sin 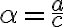 cos
cos 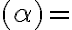 cos
cos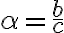
Kosínus ostrého uhla v pravouhlom trojuholníku je pomer dĺžky priľahlej odvesny ostrého uhla k dĺžke prepony.
 applet
applet  sin
sin 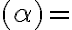 sin
sin 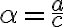 cos
cos 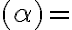 cos
cos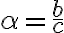
Tangens ostrého uhla v pravouhlom trojuholníku je pomer dĺžok protiľahlej a priľahlej odvesny ostrého uhla:
tg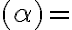 tg
tg 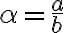
Kotangens ostrého uhla v pravouhlom trojuholníku je pomer dĺžok priľahlej a protiľahlej odvesny ostrého uhla:
cotg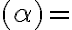 cotg
cotg 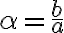
tg
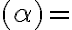 tg
tg 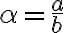
Kotangens ostrého uhla v pravouhlom trojuholníku je pomer dĺžok priľahlej a protiľahlej odvesny ostrého uhla:
cotg
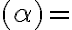 cotg
cotg 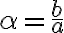
Doplňte applet pre hodnoty funkcie tangens a kotangens.
Kosínus je pomer priľahlej odvesny k prepone. Priľahlá k uhlu 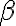 je odvesna
je odvesna  . Preto bude
. Preto bude
cos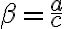
využijúc vzťah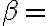 90
90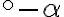 dostaneme
dostaneme
sin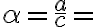 cos
cos 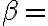 cos (90
cos (90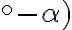 .
.
Vzťahy medzi sin a cos resp. tg a cotg
sin( ) = cos(90
) = cos(90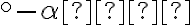 ); cos(
); cos( ) = sin(90
) = sin(90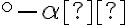 )
)
tg( ) = cotg(90
) = cotg(90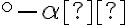 ); cotg(
); cotg( ) = tg(90
) = tg(90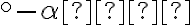 )
)
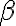 je odvesna
je odvesna  . Preto bude
. Preto bude
cos
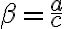
využijúc vzťah
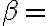 90
90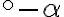 dostaneme
dostaneme
sin
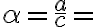 cos
cos 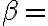 cos (90
cos (90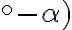 .
. Vzťahy medzi sin a cos resp. tg a cotg
sin(
 ) = cos(90
) = cos(90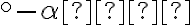 ); cos(
); cos( ) = sin(90
) = sin(90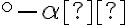 )
)
tg(
 ) = cotg(90
) = cotg(90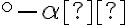 ); cotg(
); cotg( ) = tg(90
) = tg(90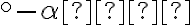 )
)
Úlohy
Riešte nasledujúce úlohy
- Zostrojte pravouhlý trojuholník
 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole
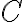 tak, aby platilo
tak, aby platilo 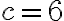 a sin
a sin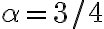 . .
. . - Zostrojte pravouhlý trojuholník
 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole
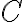 tak, aby platilo
tak, aby platilo 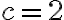 a
a 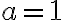 . Zostrojte obraz
. Zostrojte obraz
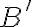 bodu
bodu
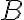 v osovej súmernosti
v osovej súmernosti 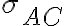 . Zostrojte štvorec
. Zostrojte štvorec
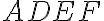 tak, aby body
tak, aby body
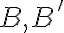 ležali na stranách
ležali na stranách
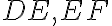 . Riešenie Tu
. Riešenie Tu - Využitím rovnostranného trojuholníka vypočítajte sin(30°), cos(30°), tg(30°), cotg(30°).
- V pravouhlom trojuholníku
 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole
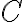 je dané
je dané 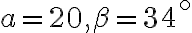 . Vypočítajte
. Vypočítajte  a
a 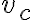 .
. - Je daná kružnica
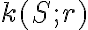 , kde
, kde 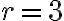 , a bod
, a bod
 s
s
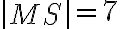 . Vypočítajte veľkosť uhla, ktorý zvierajú dotyčnice z bodu
. Vypočítajte veľkosť uhla, ktorý zvierajú dotyčnice z bodu
 ku kružnici
ku kružnici  .
.
Riešenie úlohy 3
Nech rovnostranný trojuholník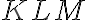 má stranu
má stranu 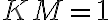 . Výšku trojuholníka vypočítame pomocou Pytagorovej vety.
. Výšku trojuholníka vypočítame pomocou Pytagorovej vety.
Využitím pravouhlého rovnoramenného trojuholníka vypočítajte hodnoty goniometrických funkcií pre uhol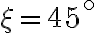 .
.
Nech rovnostranný trojuholník
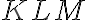 má stranu
má stranu 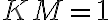 . Výšku trojuholníka vypočítame pomocou Pytagorovej vety.
. Výšku trojuholníka vypočítame pomocou Pytagorovej vety. Využitím pravouhlého rovnoramenného trojuholníka vypočítajte hodnoty goniometrických funkcií pre uhol
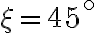 .
.Zobrazenie - vlastnosti
Zobrazenie množiny reálnych čísel na jednotkovú kružnicu - vlastnosti
Ukážeme, že zobrazenie nie je injektívne. Dvom rôznym reálnym číslam môžeme priradiť ten istý bod.
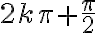 sa zobrazia do bodu
sa zobrazia do bodu 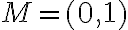 pre
pre 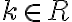 . Zobrazenie nie je injektívne.
. Zobrazenie nie je injektívne.
Ku každému bodu kružnice v kladnom zmysle (proti smeru hodinových ručičiek) existuje kladné reálne číslo, ktoré je rovné dĺžke oblúka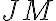 . Zobrazenie je surjektívne.
. Zobrazenie je surjektívne.
- Skúmajme, do ktorého bodu jednotkovej kružnice sa zobrazí číslo
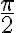 .
.
- Obvod jednotkovej kružnice je rovný číslu
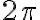 .
. - Dĺžka oblúka
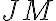 predstavuje
predstavuje 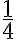 štvrtinu dĺžky celej kružnice (bod
štvrtinu dĺžky celej kružnice (bod 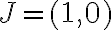 ).
). - Číslo
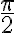 je
je 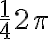 , čo predstavuje štvrtinu celého obvodu kružnice
, čo predstavuje štvrtinu celého obvodu kružnice - Preto sa číslo
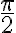 zobrazí do bodu
zobrazí do bodu  .
. - Uvažujme o čísle
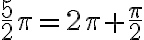 , čo predstavuje jeden a štvrť obvodu kružnice.
, čo predstavuje jeden a štvrť obvodu kružnice. - Preto sa aj číslo
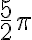 zobrazí do bodu
zobrazí do bodu 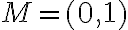 . Celá kružnica plus jedna jej štvrtina.
. Celá kružnica plus jedna jej štvrtina.
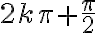 sa zobrazia do bodu
sa zobrazia do bodu 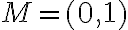 pre
pre 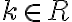 . Zobrazenie nie je injektívne.
. Zobrazenie nie je injektívne.
Ku každému bodu kružnice v kladnom zmysle (proti smeru hodinových ručičiek) existuje kladné reálne číslo, ktoré je rovné dĺžke oblúka
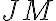 . Zobrazenie je surjektívne.
. Zobrazenie je surjektívne.
Záver
Zobrazenie množiny reálnych čísel na jednotkovú kružnicu je surjektívne ale nie je injektívne.
Zobrazenie množiny reálnych čísel na jednotkovú kružnicu je surjektívne ale nie je injektívne.
Úlohy
Riešte nasledujúce úlohy
- Ktorý bod bude priradený číslu
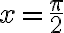 ?
? - Určte všetky reálne čísla, ktorým je na jednotkovej kružnici priradený bod
 podľa obrázka. Bod
podľa obrázka. Bod  leží na osi II. kvadrantu.
leží na osi II. kvadrantu.
- Ktoré body jednotkovej kružnice sú priradené číslam
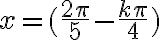 , kde
, kde 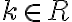 ?
? - Určte všetky reálne čísla
 , ktorým je priradený rovnaký bod jednotkovej kružnice ako číslu
, ktorým je priradený rovnaký bod jednotkovej kružnice ako číslu 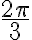 a (
a (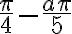 ).
).
Riešenie úlohy č. 1
Prevod stupňov na radiány
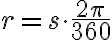 ,
,
kde je veľkosť uhla v radiánoch a
je veľkosť uhla v radiánoch a 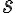 je veľkosť uhla v stupňoch
je veľkosť uhla v stupňoch
Prevod radiánov na stupne
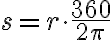 sr
sr
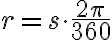 ,
,
kde
 je veľkosť uhla v radiánoch a
je veľkosť uhla v radiánoch a 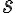 je veľkosť uhla v stupňoch
je veľkosť uhla v stupňoch
Prevod radiánov na stupne
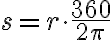 sr
sr
Definície pomocou kružnice
V predchádzajúcej časti sme definovali zobrazenie, ktoré každému reálnemu číslu  priradí bod
priradí bod ![M = [M_x; M_y] M = [M_x; M_y]](https://lms.umb.sk/filter/tex/pix.php/2e118a92f2e9767a264824dcfe1cc7b1.png) jednotkovej kružnice.
jednotkovej kružnice.
Goniometrické funkcie môžeme/vieme definovať pre ľubovoľne veľký uhol pomocou jednotkovej kružnice.
 priradí bod
priradí bod ![M = [M_x; M_y] M = [M_x; M_y]](https://lms.umb.sk/filter/tex/pix.php/2e118a92f2e9767a264824dcfe1cc7b1.png) jednotkovej kružnice.
jednotkovej kružnice.
Goniometrické funkcie môžeme/vieme definovať pre ľubovoľne veľký uhol pomocou jednotkovej kružnice.
Funkcia sínus a kosínus
Nech je ľubovoľné reálne číslo a nech
je ľubovoľné reálne číslo a nech 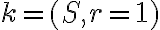 je jednotková kružnica. Potom
je jednotková kružnica. Potom
sin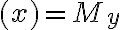 a cos
a cos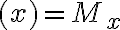 .
.
Nech
 je ľubovoľné reálne číslo a nech
je ľubovoľné reálne číslo a nech 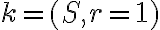 je jednotková kružnica. Potom
je jednotková kružnica. Potom
sin
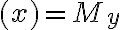 a cos
a cos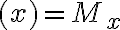 .
.
Grafy funkcií sínus a kosínus
Vlastnosti sínus/kosínus
Definície funkcií sínus a kosínus pomocou jednotkovej kružnice zodpovedá definícii pre ostrý uhol v pravouhlom trojuholníku.
V pravouhlom trojuholníku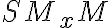 s ostrým uhlom
s ostrým uhlom  má protiľahlá odvesna veľkosť
má protiľahlá odvesna veľkosť
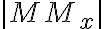 , čo predstavuje -
, čo predstavuje - 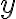 -ovú súradnicu bodu
-ovú súradnicu bodu
 . Prepona má veľkosť
. Prepona má veľkosť
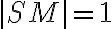 . Potom
. Potom
sin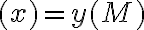 .
.
V pravouhlom trojuholníku
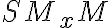 s ostrým uhlom
s ostrým uhlom  má protiľahlá odvesna veľkosť
má protiľahlá odvesna veľkosť
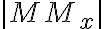 , čo predstavuje -
, čo predstavuje - 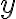 -ovú súradnicu bodu
-ovú súradnicu bodu
 . Prepona má veľkosť
. Prepona má veľkosť
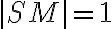 . Potom
. Potom
sin
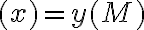 .
.
Symetria sin a cos
sin(π + x) = − sin(x), cos(π + x) = − cos(x)
sin(2π − x) = − sin(x), cos(2π − x) = cos(x)
Dôležité hodnoty pre 0° 30° 45° 60° 90°
sin(x)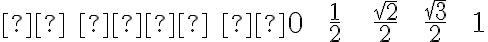
cos(x)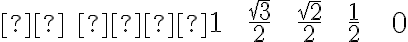
sin(π + x) = − sin(x), cos(π + x) = − cos(x)
sin(2π − x) = − sin(x), cos(2π − x) = cos(x)
Dôležité hodnoty pre 0° 30° 45° 60° 90°
sin(x)
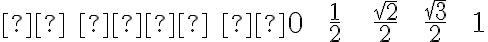
cos(x)
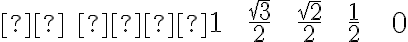
Autor: Daniel Mentrard. Dostupné Tu
Posunutie grafu
Vzorce
Súčtové vzorce pre sínus a kosínus
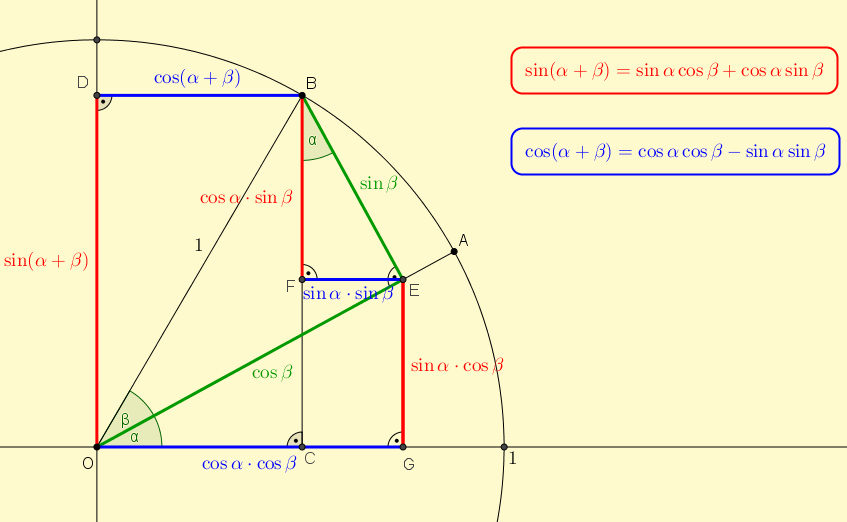
Stiahnite si applet od M. Vinkléra Tu
Cvičenie
Poznámky
- ...
- ...
...

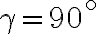
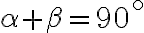
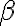
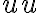
![J=[1, 0] J=[1, 0]](https://lms.umb.sk/filter/tex/pix.php/4e19bf474dd53619314042bb84f44344.png)