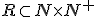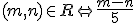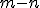Konštrukcia číselných oborov - prirodzené čísla
Číselné obory
Príklad rozšírenia
Nech 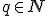 je ľubovoľné prirodzené číslo rôzne od nuly a
je ľubovoľné prirodzené číslo rôzne od nuly a 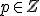 je ľubovoľné celé číslo. Množinu racionálnych
čísel
je ľubovoľné celé číslo. Množinu racionálnych
čísel 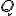 môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
Takéto dvojice![\small [p,q] \small [p,q]](https://lms.umb.sk/filter/tex/pix.php/f638a7987a9a0506caf6e3e19494ee83.png) môžeme interpretovať aj ako zlomky
môžeme interpretovať aj ako zlomky 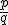 .
.
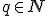 je ľubovoľné prirodzené číslo rôzne od nuly a
je ľubovoľné prirodzené číslo rôzne od nuly a 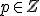 je ľubovoľné celé číslo. Množinu racionálnych
čísel
je ľubovoľné celé číslo. Množinu racionálnych
čísel 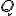 môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
Takéto dvojice
![\small [p,q] \small [p,q]](https://lms.umb.sk/filter/tex/pix.php/f638a7987a9a0506caf6e3e19494ee83.png) môžeme interpretovať aj ako zlomky
môžeme interpretovať aj ako zlomky 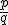 .
.
- Na množine zlomkov
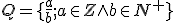 potom definujme rovnosť zlomkov takto:
potom definujme rovnosť zlomkov takto:
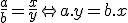
- Ukážte, že rovnosť zlomkov je relácia ekvivalencie, ktorá množinu všetkých zlomkov rozdelí do disjunktných podmnožín.
- Popíšte tento rozklad.
- Napríklad trieda rozkladu, ktorá obsahuje zlomok
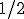 bude obsahovať aj zlomky
bude obsahovať aj zlomky 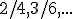 .
. - Všetky zlomky z tejto podmnožiny sa navzájom rovnajú.
- Preto stačí vybrať jeden zlomok, ktorý bude reprezentovať túto podmnožinu a vyhlásiť ho za racionálne číslo.
- Za „reprezentanta“ racionálneho čísla zvolíme každý zlomok
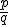 , ktorý je v základnom tvare. Teda, keď čísla
, ktorý je v základnom tvare. Teda, keď čísla
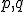 sú nesúdeliteľné a zárove
sú nesúdeliteľné a zárove 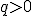 . Inými slovami, ak zlomok
. Inými slovami, ak zlomok 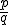 už nemôžeme krátiť.
už nemôžeme krátiť. - Množina racionálnych čísel
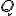 je množina všetkých zlomkov v základnom tvare.
je množina všetkých zlomkov v základnom tvare.
Uveďme aj matematický zápis takejto množiny: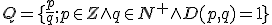
- Operácie sčítanie a násobenie racionálnych čísel potom môžeme zaviesť pomocou pravidiel na súčet a súčin zlomkov. Definujte tieto operácie.
Poznámka.
Takýto spôsob zavedenia racionálnych čísel pomocou zlomkov je vhodný pre školskú matematiku, keďže žiaci sa oboznamujú najskôr so zlomkami. Pozri Fraction Book.
Takýto spôsob zavedenia racionálnych čísel pomocou zlomkov je vhodný pre školskú matematiku, keďže žiaci sa oboznamujú najskôr so zlomkami. Pozri Fraction Book.