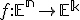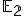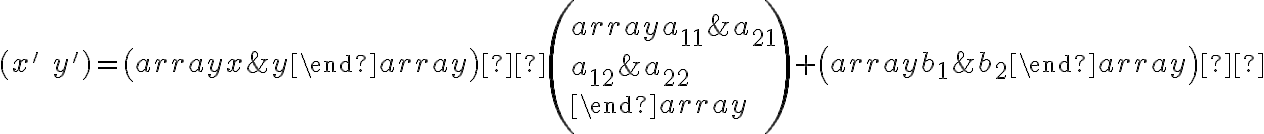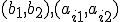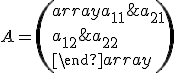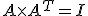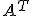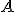Zhodnostné a podobnostné zobrazenia
Zhodnostné zobrazenia
Analytické vyjadrenia zhodnostných zobrazení
Geometrické resp. konštrukčné vlastnosti zhodnostných zobrazení nájdete
Tu.
Definícia
Zobrazenie v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body
v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body 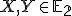 a ich obrazy
a ich obrazy 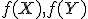 platí
platí
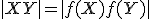 .
.
Inými slovami zhodné zobrazenia zachovávajú vzdialenosti bodov.
Zobrazenie
 v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body
v rovine budeme nazývať zhodnostné zobrazenie, ak pre každé dva body 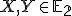 a ich obrazy
a ich obrazy 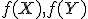 platí
platí
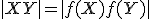 .
.
Inými slovami zhodné zobrazenia zachovávajú vzdialenosti bodov.
Dôkaz
Treba dokázať, že zhodnostné zobrazenie spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech
spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech  sú kolineárne body
sú kolineárne body  , potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov
, potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov  platí
platí 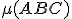 . Bod
. Bod 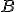 leží medzi bodmi
leží medzi bodmi 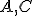 .
.
Ukážeme, že body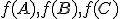 sú kolineárne a zároveň platí
sú kolineárne a zároveň platí 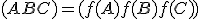 .
.
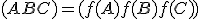 . Načrtnite si obrázok.
. Načrtnite si obrázok.
Treba dokázať, že zhodnostné zobrazenie
 spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech
spĺňa podmienku zachovania kolineárnosti a deliaceho pomeru.
Nech 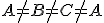 sú kolineárne body
sú kolineárne body  , potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov
, potom zrejme aj body (\small f(A), f(B),f(C) \) sú navzájom rôzne.
Bez ujmy na obecnosti môžeme predpokladať, že pre usporiadanie bodov 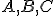 platí
platí 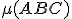 . Bod
. Bod 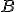 leží medzi bodmi
leží medzi bodmi 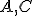 .
.
Ukážeme, že body
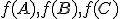 sú kolineárne a zároveň platí
sú kolineárne a zároveň platí 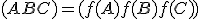 .
.
- Prvú časť tvrdenia dokážeme sporom. Nech body
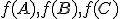 nie sú kolineárne, potom vytvárajú trojuholník a
na základe trojuholníkovej nerovnosti dostaneme spor.
nie sú kolineárne, potom vytvárajú trojuholník a
na základe trojuholníkovej nerovnosti dostaneme spor. - Teda body
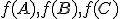 ležia na jednej priamke. Pre ich usporiadanie môžu nastať dva prípady, z ktorých iba prípad, keď bod
ležia na jednej priamke. Pre ich usporiadanie môžu nastať dva prípady, z ktorých iba prípad, keď bod 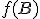 leží medzi bodmi
leží medzi bodmi 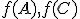 vyhovuje podmienkam:
vyhovuje podmienkam:
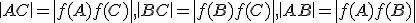 .
.
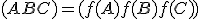 . Načrtnite si obrázok.
. Načrtnite si obrázok.
Osová súmernosť je oproti ostatným zhodným zobrazeniam niečím výnimočná. Má jednu veľmi zaujímavú vlastnosť, skladaním osových súmerností sa dajú získať
všetky zhodné zobrazenia v rovine. Z toho dôvodu začneme analytickým vyjadrením osovej súmernosti.
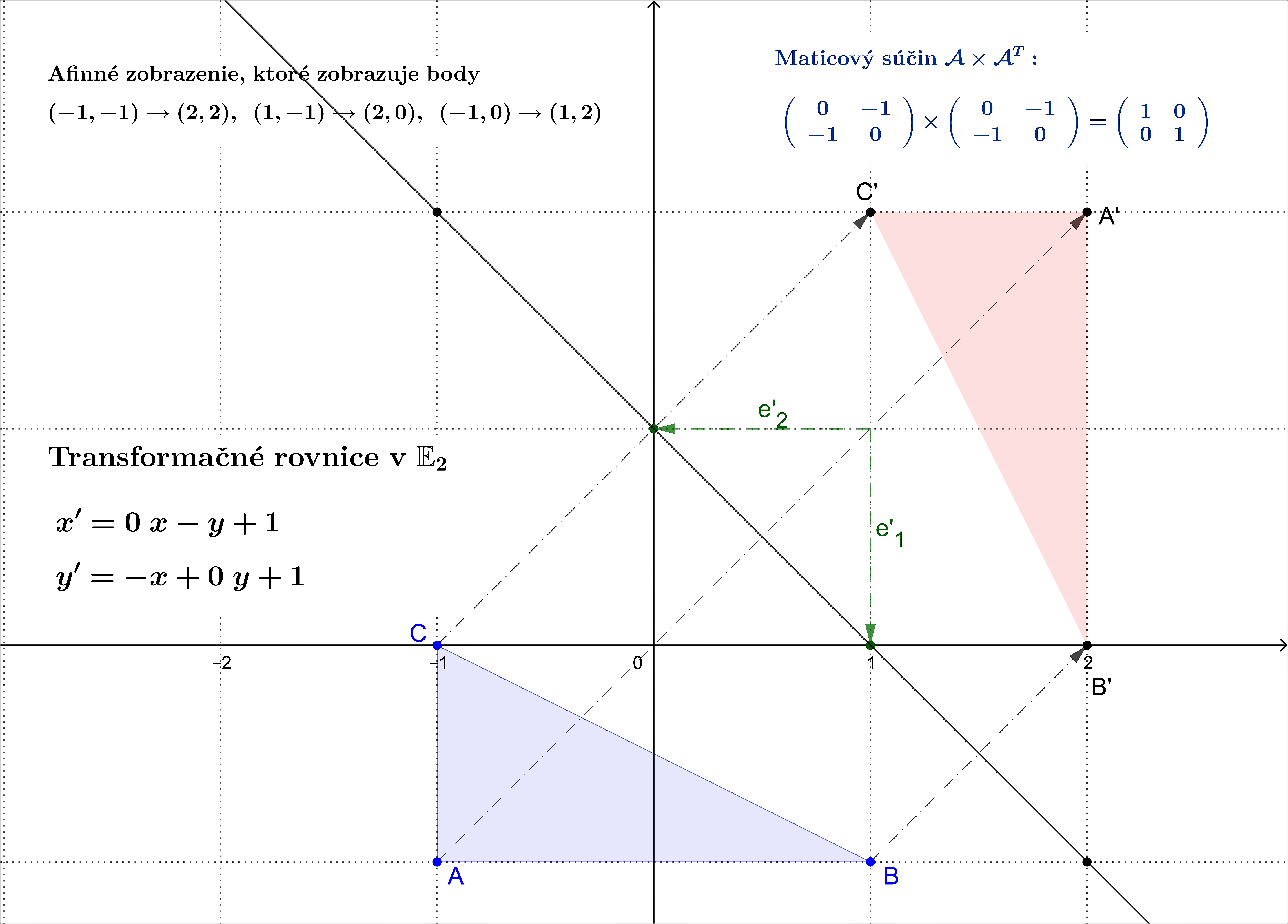
Geometrická interpretácia osovej súmernosti ako afinnej transformácie: Odvodenie rovníc Tu, Verzia "Repér" Tu

Geometrická interpretácia osovej súmernosti ako afinnej transformácie: Odvodenie rovníc Tu, Verzia "Repér" Tu