Voľné rovnobežné premietanie
Voľné rovnobežné premietanie
Medzi dôležité tematické oblasti stereometrie zaraďujeme aj princípy zobrazovania útvarov (telies) do roviny (priemetne). Pripomeňme si, že základný trojrozmerný geometrický útvar je jednoznačne určený svojimi význačnými bodmi1).
Obrazom geometrického útvaru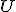 vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar
vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar 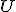 určený.
určený.
Obrazom geometrického útvaru
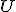 vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar
vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar 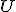 určený.
určený.
Nech 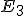 je trojrozmerný euklidovský priestor a nech rovina
je trojrozmerný euklidovský priestor a nech rovina 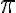 je jeho podmnožinou. Ďalej nech je daná pevná priamka
je jeho podmnožinou. Ďalej nech je daná pevná priamka 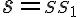 , ktorá je rôznobežná s rovinou
, ktorá je rôznobežná s rovinou  .
.
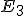 je trojrozmerný euklidovský priestor a nech rovina
je trojrozmerný euklidovský priestor a nech rovina 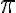 je jeho podmnožinou. Ďalej nech je daná pevná priamka
je jeho podmnožinou. Ďalej nech je daná pevná priamka 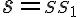 , ktorá je rôznobežná s rovinou
, ktorá je rôznobežná s rovinou  .
.
Definícia
- voľné rovnobežné premietanie2) (VRP)
Zobrazenie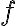 množiny všetkých bodov priestoru
množiny všetkých bodov priestoru 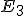 , ktoré každému bodu
, ktoré každému bodu  priradí priesečník
priradí priesečník 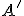 priamky
priamky 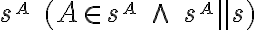 s rovinou
s rovinou  , nazveme voľné rovnobežné premietanie do roviny
, nazveme voľné rovnobežné premietanie do roviny  so smerom
so smerom 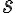 (označujeme
(označujeme 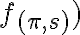 .
.
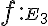
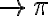 ;
; 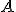
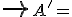
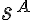
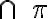 , pričom
, pričom 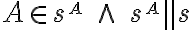
Zobrazenie
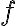 množiny všetkých bodov priestoru
množiny všetkých bodov priestoru 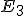 , ktoré každému bodu
, ktoré každému bodu  priradí priesečník
priradí priesečník 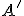 priamky
priamky 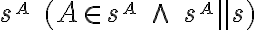 s rovinou
s rovinou  , nazveme voľné rovnobežné premietanie do roviny
, nazveme voľné rovnobežné premietanie do roviny  so smerom
so smerom 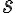 (označujeme
(označujeme 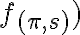 .
.
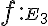
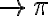 ;
; 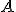
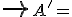
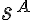
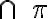 , pričom
, pričom 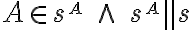
Definície
- Priamku
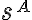 nazývame premietajúca priamka bodu
nazývame premietajúca priamka bodu  alebo smer premietania, rovinu
alebo smer premietania, rovinu  priemetňa.
Bod
priemetňa.
Bod 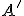
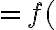
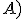 sa nazýva rovnobežný priemet bodu
sa nazýva rovnobežný priemet bodu  v danom rovnobežnom premietaní
v danom rovnobežnom premietaní 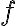 .
. - Rovnobežným priemetom
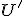 ľubovoľného geometrického útvaru
ľubovoľného geometrického útvaru 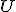 sa bude nazývať množina rovnobežných priemetov všetkých bodov útvaru
sa bude nazývať množina rovnobežných priemetov všetkých bodov útvaru 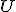 .
. - Nech
 je ľubovoľná priamka, ktorá je s priemetňou
je ľubovoľná priamka, ktorá je s priemetňou  rôznobežná. Jej priesečník s priemetňou budeme nazývať stopník priamky
rôznobežná. Jej priesečník s priemetňou budeme nazývať stopník priamky  (označenie
(označenie 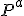 ). Analogicky priesečnicu ľubovoľnej roviny
). Analogicky priesečnicu ľubovoľnej roviny  (
(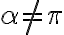 ) s priemetňou budeme nazývať stopa roviny
) s priemetňou budeme nazývať stopa roviny  (označenie
(označenie 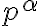 ).
).
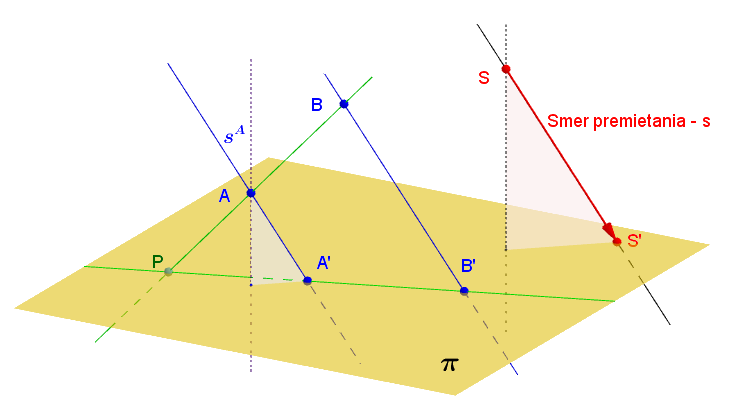
Poznámka.
V prípade, že priamka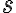 je kolmá na priemetňu s priemetňou
je kolmá na priemetňu s priemetňou  hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
V prípade, že priamka
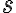 je kolmá na priemetňu s priemetňou
je kolmá na priemetňu s priemetňou  hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
Cvičenie
Zostrojte obrazy troch nekolineárnych bodov vo VRP. Nájdite stopu roviny, ktorá je určená týmito troma bodmi. Zadanie si otvorte Tu.
Zostrojte obrazy troch nekolineárnych bodov vo VRP. Nájdite stopu roviny, ktorá je určená týmito troma bodmi. Zadanie si otvorte Tu.
____________________________________________________________________________________________________
1) Napríklad hranol je určený svojimi vrcholmi, valec stredmi podstáv a jedným ľubovoľným bodom kružnice určujúcej podstavu, a pod.
2) Doporučená literatúra: Hromadová, J.: Deskriptívní geometrie na MFF UK. Grant FRVŠ, UK Praha 2013. Dostupné na internete Tu.
1) Napríklad hranol je určený svojimi vrcholmi, valec stredmi podstáv a jedným ľubovoľným bodom kružnice určujúcej podstavu, a pod.
2) Doporučená literatúra: Hromadová, J.: Deskriptívní geometrie na MFF UK. Grant FRVŠ, UK Praha 2013. Dostupné na internete Tu.
...
