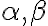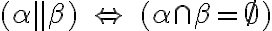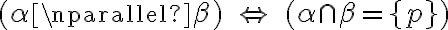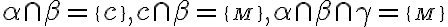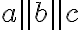Euklidovský priestor
Rovnobežnosť útvarov
Vzájomná poloha rovín
Dohovor
Ak sa medzi skúmanou trojicou rovín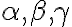 vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme
vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme 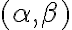 (lexikografický prístup).
(lexikografický prístup).
To neznamená, že dvojicou rovnobežných rovín nemôže byť dvojica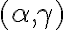 alebo
alebo 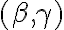 .
.
Ak sa medzi skúmanou trojicou rovín
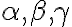 vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme
vyskytne dvojica rovín navzájom rovnobežných, tak bez ujmy na obecnosti ju označíme 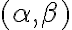 (lexikografický prístup).
(lexikografický prístup).
To neznamená, že dvojicou rovnobežných rovín nemôže byť dvojica
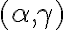 alebo
alebo 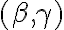 .
.
Klasifikácia vzájomnej polohy troch rovín
-
Nech platí
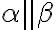 .
Pre rovinu
.
Pre rovinu 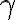 potom platí: alebo
potom platí: alebo 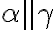 alebo
alebo 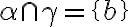
- Uvažujme o rovinách
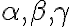 , pre ktoré
, pre ktoré 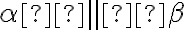 ,
, 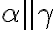 . Obrázok vľavo. Z tranzitívnosti relácie rovnobežnosti rovín vyplýva záver:
. Obrázok vľavo. Z tranzitívnosti relácie rovnobežnosti rovín vyplýva záver: 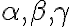 je trojica navzájom rôznych rovnobežných rovín.
je trojica navzájom rôznych rovnobežných rovín. - Nech platí:
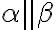 ∧
∧ 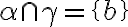 . Dôsledkom je rôznobežnosť rovín
. Dôsledkom je rôznobežnosť rovín 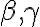 (v opačnom prípade by boli všetky tri roviny navzájom rovnobežné, čo je spor s predpokladom).
Je zrejmé, že priesečnice dvojíc rovín
(v opačnom prípade by boli všetky tri roviny navzájom rovnobežné, čo je spor s predpokladom).
Je zrejmé, že priesečnice dvojíc rovín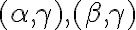 sú navzájom rovnobežné priamky. (Odôvodnite.)
Záver: Roviny
sú navzájom rovnobežné priamky. (Odôvodnite.)
Záver: Roviny 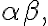 sú navzájom rovnobežné a rovina
sú navzájom rovnobežné a rovina 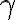 ich pretína v dvoch navzájom rovnobežných priamkach
ich pretína v dvoch navzájom rovnobežných priamkach 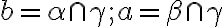 . Obr. vpravo.
. Obr. vpravo. - Nech platí:
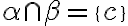 .
Skúmajme vzájomnú polohu priamky
.
Skúmajme vzájomnú polohu priamky  s rovinou
s rovinou 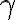 . Môže nastať práve jeden z prípadov:
(
. Môže nastať práve jeden z prípadov:
(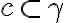 alebo
alebo 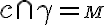 alebo
alebo 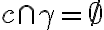 .
.
Tvrdenie. Existuje päť vzájomných polôh troch navzájom rôznych rovín:
- všetky tri roviny sú navzájom rovnobežné
- dve rovnobežné roviny pretína tretia v navzájom rovnobežných priamkach
- všetky tri roviny majú spoločnú práve jednu priamku (os zväzku rovín)
- všetky tri roviny majú spoločný práve jeden bod
- všetky dvojice rovín sú navzájom rôznobežné roviny a ich priesečnice sú navzájom rôzne rovnobežné priamky.
______________________________________________________________
Obrázky sú prevzaté z publikácie
Klenková, P.: Stereometria – elementárna geometria trojrozmerného euklidovského priestoru, Diplomová práca, UK FMFI, Bratislava 2006
Obrázky sú prevzaté z publikácie
Klenková, P.: Stereometria – elementárna geometria trojrozmerného euklidovského priestoru, Diplomová práca, UK FMFI, Bratislava 2006
... ...