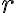GeoGebra v algebraickom učive
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | GeoGebra v algebraickom učive |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | nedeľa, 28 apríla 2024, 22:10 |
Opis
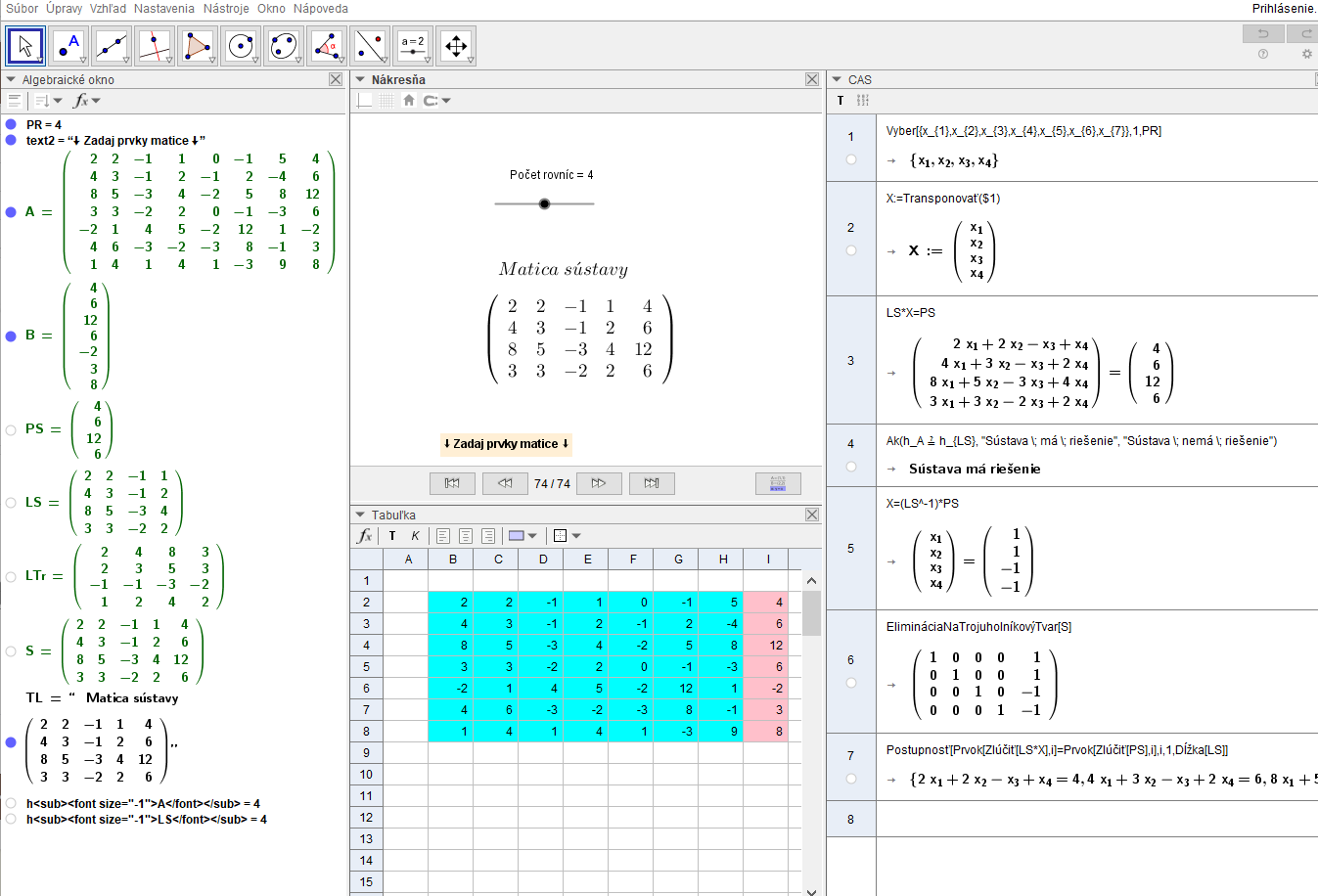
GeoGebra
Pracovné prostredie
Pri algebraických výpočtoch môžeme využívame hlavne tri prostredia:
- Algebraické okno
- Počítačový algebraický systém (CAS)
- Práca s tabuľkami, maticami a so zoznamami prvkov
Pri práci s textom s výhodou využívame rôzne formáty textu. Napríklad pri zapisovaní riešenia rovníc môžeme použiť
Algebraické okno
Riešenie lineárnej rovnice
Vytvorte applety na riešenie
- kvadratických rovníc a nerovníc
- nerovníc s absolútnou hodnotou
- sústavy dvoch lineárnych rovníc
Sústava lineárnych rovníc
Rovnice tvaru
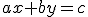 , kde
, kde 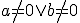
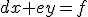 , kde
, kde 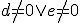
nazývame sústavou dvoch lineárnych rovníc s dvoma neznámymi.
Pri riešení sústavy dvoch rovníc s dvoma neznámymi využívame 3 metódy:
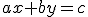 , kde
, kde 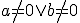
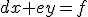 , kde
, kde 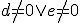
nazývame sústavou dvoch lineárnych rovníc s dvoma neznámymi.
Pri riešení sústavy dvoch rovníc s dvoma neznámymi využívame 3 metódy:
- dosadzovaciu (substitučnú) metódu;
- sčítaciu (adičnú) metódu;
- porovnávaciu (komparačnú) metódu.
Dosadzovacia (substitučná) metóda.
Táto metóda spočíva v tom, že z jednej rovnice si vyjadríme jednu neznámu a výraz ktorý takto dostaneme, dosadíme za túto neznámu do druhej rovnice.
Takto dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Následne dosadením vypočítame i druhú neznámu.
Táto metóda spočíva v tom, že z jednej rovnice si vyjadríme jednu neznámu a výraz ktorý takto dostaneme, dosadíme za túto neznámu do druhej rovnice.
Takto dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Následne dosadením vypočítame i druhú neznámu.
Riešenie.
Z prvej rovnice si vyjadríme napr. neznámu :
:
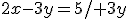
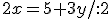
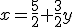
Výraz, ktorý sme získali dosadíme do druhej rovnice za neznámu :
:
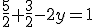
Získali sme lineárnu rovnicu s jednou neznámou, ktorú vyriešime:
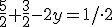
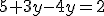
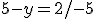
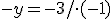
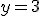
Získanú neznámu dosadíme do upravenej 1. rovnice a vypočítame neznámu :
:
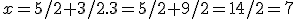
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc:
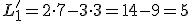
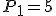
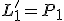
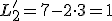
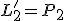
Riešením danej sústavy je usporiadaná dvojica![\small [x; y] = [7; 3]. \small [x; y] = [7; 3].](https://lms.umb.sk/filter/tex/pix.php/5c33cebd92a4fd94aa4520ff354b28b7.png)
Z prvej rovnice si vyjadríme napr. neznámu
 :
: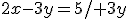
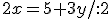
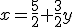
Výraz, ktorý sme získali dosadíme do druhej rovnice za neznámu
 :
:
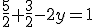
Získali sme lineárnu rovnicu s jednou neznámou, ktorú vyriešime:
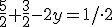
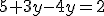
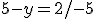
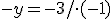
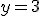
Získanú neznámu dosadíme do upravenej 1. rovnice a vypočítame neznámu
 :
: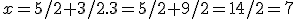
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc:
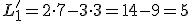
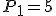
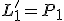
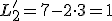
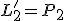
Riešením danej sústavy je usporiadaná dvojica
![\small [x; y] = [7; 3]. \small [x; y] = [7; 3].](https://lms.umb.sk/filter/tex/pix.php/5c33cebd92a4fd94aa4520ff354b28b7.png)
Cvičenie.
Riešte sústavu rovníc
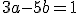
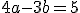
s neznámymi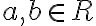 dosadzovacou metódou.
dosadzovacou metódou.
Riešenie:
Riešením danej sústavy je usporiadaná dvojica [a; b] = [; ].
Riešte sústavu rovníc
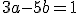
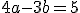
s neznámymi
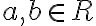 dosadzovacou metódou.
dosadzovacou metódou.Riešenie:
Riešením danej sústavy je usporiadaná dvojica [a; b] = [; ].
Sčítacia (adičná) metóda.
Táto metóda spočíva v tom, že každú rovnicu po úprave na základný tvar napr.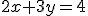 vhodne násobíme tak, aby po sčítaní oboch rovníc jedna neznáma „vypadla“.
vhodne násobíme tak, aby po sčítaní oboch rovníc jedna neznáma „vypadla“.
Takto dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Pri „čistej“ sčítacej metóde to isté vykonáme i s druhou neznámou. V praxi je často využívaná kombinácia sčítacej a dosadzovacej metódy, čiže jednu neznámu určíme sčítacou metódou a druhú dosadením už známej hodnoty do niektorej z rovníc.
I túto metódu si radšej ukážeme na konkrétnom príklade.
Táto metóda spočíva v tom, že každú rovnicu po úprave na základný tvar napr.
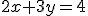 vhodne násobíme tak, aby po sčítaní oboch rovníc jedna neznáma „vypadla“.
vhodne násobíme tak, aby po sčítaní oboch rovníc jedna neznáma „vypadla“.Takto dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Pri „čistej“ sčítacej metóde to isté vykonáme i s druhou neznámou. V praxi je často využívaná kombinácia sčítacej a dosadzovacej metódy, čiže jednu neznámu určíme sčítacou metódou a druhú dosadením už známej hodnoty do niektorej z rovníc.
I túto metódu si radšej ukážeme na konkrétnom príklade.
Riešenie.
Chceme určiť napr. neznámu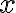 , teda potrebujeme, aby „vypadla“ neznáma
, teda potrebujeme, aby „vypadla“ neznáma 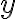 . Násobíme teda prvú rovnicu číslom -2 a druhú rovnicu číslom 3.
. Násobíme teda prvú rovnicu číslom -2 a druhú rovnicu číslom 3.
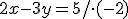
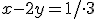
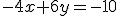
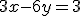
Teraz obe rovnice sčítame:
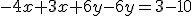
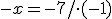
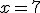
Ak chceme kombinovať sčítaciu a dosadzovaciu metódu, tak hodnotu neznámej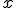 , ktorú sme získali, dosadíme napr. do druhej rovnice za neznámu
, ktorú sme získali, dosadíme napr. do druhej rovnice za neznámu 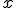 :
:
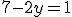 a z toho
a z toho 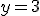 .
.
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc:
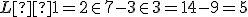
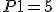
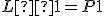
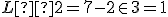
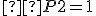
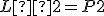
Riešením danej sústavy je usporiadaná dvojica![\small [x; y] = [7; 3] \small [x; y] = [7; 3]](https://lms.umb.sk/filter/tex/pix.php/0c1d269107cf143d33d838c7852a6edc.png) .
.
Chceme určiť napr. neznámu
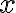 , teda potrebujeme, aby „vypadla“ neznáma
, teda potrebujeme, aby „vypadla“ neznáma 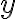 . Násobíme teda prvú rovnicu číslom -2 a druhú rovnicu číslom 3.
. Násobíme teda prvú rovnicu číslom -2 a druhú rovnicu číslom 3.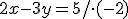
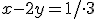
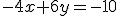
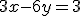
Teraz obe rovnice sčítame:
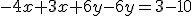
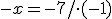
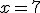
Ak chceme kombinovať sčítaciu a dosadzovaciu metódu, tak hodnotu neznámej
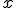 , ktorú sme získali, dosadíme napr. do druhej rovnice za neznámu
, ktorú sme získali, dosadíme napr. do druhej rovnice za neznámu 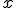 :
: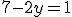 a z toho
a z toho 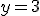 .
.Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc:
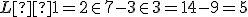
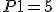
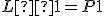
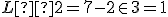
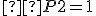
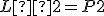
Riešením danej sústavy je usporiadaná dvojica
![\small [x; y] = [7; 3] \small [x; y] = [7; 3]](https://lms.umb.sk/filter/tex/pix.php/0c1d269107cf143d33d838c7852a6edc.png) .
.
Cvičenie:
Riešte sústavu rovníc
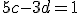
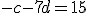
s neznámymi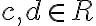 kombináciou sčítacej a dosadzovacej metódy.
kombináciou sčítacej a dosadzovacej metódy.
Riešenie:
Riešením danej sústavy je usporiadaná dvojica![\small [c; d] = [ ; ]. \small [c; d] = [ ; ].](https://lms.umb.sk/filter/tex/pix.php/e2a2c8c46c5e019a1c91e35579d30d2b.png)
Riešte sústavu rovníc
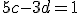
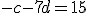
s neznámymi
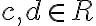 kombináciou sčítacej a dosadzovacej metódy.
kombináciou sčítacej a dosadzovacej metódy.Riešenie:
Riešením danej sústavy je usporiadaná dvojica
![\small [c; d] = [ ; ]. \small [c; d] = [ ; ].](https://lms.umb.sk/filter/tex/pix.php/e2a2c8c46c5e019a1c91e35579d30d2b.png)
Porovnávacia (komparačná) metóda:
Táto metóda spočíva v tom, že z oboch rovníc si vyjadríme tú istú neznámu. Získané výrazy porovnáme a tak dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Následne dosadením vypočítame i druhú neznámu.
Vypočítajme príklad.
Táto metóda spočíva v tom, že z oboch rovníc si vyjadríme tú istú neznámu. Získané výrazy porovnáme a tak dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Následne dosadením vypočítame i druhú neznámu.
Riešenie.
Z prvej rovnice si vyjadríme napr. neznámu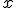 :
:
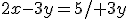
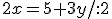
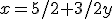
Z druhej rovnice si vyjadríme tiež neznámu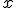 :
:
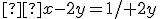
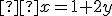
Keďže sa rovnajú ľavé strany oboch rovníc, tak sa rovnajú i pravé strany týchto rovníc, takže vytvoríme rovnicu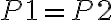 , ktorú vyriešime:
, ktorú vyriešime:
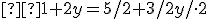
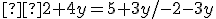
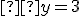
Získanú hodnotu premennej y dosadíme napr. do upravenej druhej rovnice:
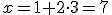
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc podobne ako v príklade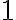 a
a 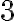 .
.
Riešením danej sústavy je usporiadaná dvojica![\small [x; y] = [7; 3] \small [x; y] = [7; 3]](https://lms.umb.sk/filter/tex/pix.php/56e0852bd472500f53cd4b8ee3633041.png) .
.
Z prvej rovnice si vyjadríme napr. neznámu
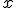 :
: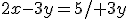
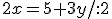
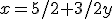
Z druhej rovnice si vyjadríme tiež neznámu
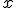 :
: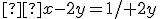
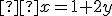
Keďže sa rovnajú ľavé strany oboch rovníc, tak sa rovnajú i pravé strany týchto rovníc, takže vytvoríme rovnicu
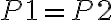 , ktorú vyriešime:
, ktorú vyriešime: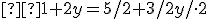
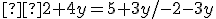
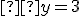
Získanú hodnotu premennej y dosadíme napr. do upravenej druhej rovnice:
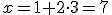
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc podobne ako v príklade
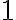 a
a 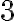 .
.Riešením danej sústavy je usporiadaná dvojica
![\small [x; y] = [7; 3] \small [x; y] = [7; 3]](https://lms.umb.sk/filter/tex/pix.php/56e0852bd472500f53cd4b8ee3633041.png) .
.Sústava - riešenie
Otvorte Tu
Kvadratické rovnice a CAS
Úprava algebraického výrazu a riešenie kvadratickej rovnice
Vytvorte zbierku na úpravu algebaických výrazov
→
Vytvorte applet, ktorý bude zobrazovať graf kvadratickej funkcie, jej vrchol a nulové body (korene odpovedajúcej kvadratickej rovnice).
Práca s textom
GeoGebra umožňuje zobrazovať text v rôznych formátoch
- Preddefinované štýly textu: Sans Serif, Serif, Bold, Kurzíva. Farby neobmedzene.
- Napríklad príkaz \textbf \textit \textcolor{00005A} {Navy} \; \textbf \textcolor{red} {Red} \; \textit \textbf \textcolor{0BDF00} {Green}
vytvorí text
GeoGebra umožňuje
- LaTeX zápisy, pričom je možné vkladať základné matematické výrazy a symboly. Užívateľ si môže vložiť vlastný TeX zápis. Pomoc pri výbere fontu TeX →
- Vytvoriť dynamický text: If( <Podmienka1>, <Text 1>, <Podmienka 2>, <Text 2>, ... , <Else (optional)> )
- Vytvorí kópiu "Text 1", keď je splnená prvá podmienka, "Text 2", ak je splnená druhá podmienka atď.
- Ak nie je splnená žiadna z podmienok a je daná Else, tento príkaz prináša kópiu Else.
- V opačnom prípade sa vráti nedefinovaná.
- Príklad: Ak (a ≟ 1, "Matthew", ≟ 2, "Larry", ≟ 3, "Vivian", "Alex")
- Pre a = 1 to vráti text "Matthew", pre a = 2 vracia "Larry", pre a = 3 "Vivian" a pre všetky ostatné hodnoty to znamená "Alex".
Návrhy appletov
V tejto kapitole prezentujeme separované modely, ktoré môžeme použiť pri výklade alebo pri precvičovaní matematických pojmov.
A: Postup pri vytváraní separovaného modelu
- Určíme motivačný background pre daný matematický pojem. Napr. teplomer ↔ záporné čísla.
- Podrobne popíšeme etapy na vytvorenie appletu v prostredí, pričom každá etapa
- predstavuje podrobný konštrukčný popis jednotlivých krokov
- obsahuje zápisy príkazov v jazyku GeoGebry
- V závere sú uvedené ukážky nami hotovených appletov
B: Odkaz na externý separovaný model
- Uvedieme stručný teoretický výklad pre danú matematickú oblasť. Napr. polárna sústava súradníc.
- Presmerujeme na materiál (book) na serveri Geogebra
Teplomer
Záporné čísla – separovaný model „Teplomer“
→
→
Postup
pri tvorbe appletu Teplomer
- Vyhľadáme vhodný obrázok teplomera a upravíme ho tak, aby v strede bol prázdny (biely) rámik. Otvorte si zadanie TeplomerZad.
- V GeoGebre vytvoríme
- dva posuvníky HORIZ, VERT, ktorými budeme posúvať obrázok
- posuvník ZVAC, ktorým budeme zväčšovať resp. zmenšovať obrázok
- dva body RDL (roh dolný ľavý), RDP (roh dolný pravý), ktorých poloha bude závislá od posuvníkov
- obrázok TeplomerObr vložíme do nákresne a ukotvíme ho bodmi RDL, RDB
- priamky LV, PV ako ľavá a pravá strana stredového rámika, v ktorom budú ukazovatele teploty (farebné obdĺžniky)
- Návrh ukazovateľov teploty - farebné obdĺžniky:
- v strede teplomera vytvoríme dynamický mnohouholník Tep1, ktorý bude predstavovať nárast teploty
- dolný pravý vrchol PocT1 mnohouholníka bude závislý od počiatočnej teploty - posuvníka PocT, vľavo od neho bod G
- horný pravý vrchol NarT1 mnohouholníka bude závislý od nárastu teploty - posuvníka NarT, vľavo od neho bod G1
- Podobne zostrojíme mnohouholník, ktorý bude predstavovať pokles teploty
- Vytvoríme zoznamy bodov Zoznam1 a čísel Zoznam2, ktoré budú reprezentovať číselnú os pre zmenu teploty
- Na číselnej osi pomocou vektorov znázorníme pokles resp. nárast teploty
- Navrhneme vhodné texty pre prácu s celými resp. so zápornými číslami
Hodiny
Návrh hodín - pomôcka pri výklade a precvičovaní pojmu uhol 
Tvorba testu
Rozbaľovacie menu
Ako používať tento súbor:
- V hlavnom menu GeoGebry si aktivujte: Algebraické okno, Nákresňa, Tabuľka
- Do tabuľky vložte texty možných odpovedí pre plánované otázky (pozri priložený applet)
- bunku
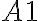 nechajte prázdnu
nechajte prázdnu - do bunky
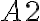 vložte (napíšte) text prvej otázky
vložte (napíšte) text prvej otázky 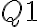 , do
, do 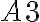 vložte
vložte 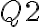 , ...
, ... - do bunky
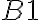 vložte (napíšte) text "Spätná väzba"
vložte (napíšte) text "Spätná väzba" - do bunky
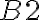 vložte (napíšte) text prvej spätnej väzby: správne resp. nesprávne, ...
vložte (napíšte) text prvej spätnej väzby: správne resp. nesprávne, ... - Vytvorte Tlačidlá: “Generovať Otázky ...” a “Reset ...” a skopírujte ich skripty z priloženého appletu
- Vytvorte potrebné zoznamy pre otázky (ZoznamOtazkaQ1) a spätnú väzbu (ZoznamSpatnaVazbaQ1). Použite pre:
- ZoznamOtazkaQ1: príkaz Zoznam alebo do vstupného poľa vložte
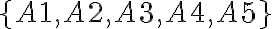
- ZoznamSpatnaVazbaQ1: príkaz Zoznam alebo do vstupného poľa vložte
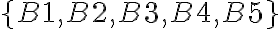
- Pre zobrazenie otázok v rozbaľovacej ponuke je potrebné v algebraickom okne:
- kliknite na príslušný zoznam
- vyberte vlastnosti
- začiarknite políčko “Kresliť v rozbaľovacom zozname”, zobrazia sa odpovedajúce texty otázok
- Vytvorenie textového poľa pre spätnú väzbu zadajte vo vstupnom poli:
- Text(Prvok(ZoznamSpatnaVazbaQ1, VybratýIndex(ZoznamOtazkaQ1)))
- Podľa potreby upravte pozície pre rozbaľovacie zoznamy a textové polia.
- Vyskúšajte tlačidlo RESET a uvidíte, že zoznamy sa vrátia späť na prvý prvok v zozname.
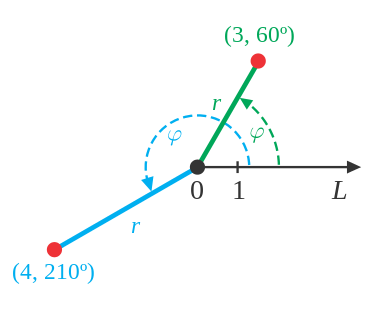
Polárna sústava súradníc
Polárna sústava súradníc →
- Sústava súradníc (tzv. polárnych súradníc) v rovine, ktorá určuje polohu bodu
 dvoma parametrami:
dvoma parametrami:
- Tento systém je založený na
- centrálnom bode
 , ktorý sa nazýva pól
, ktorý sa nazýva pól - polpriamke
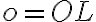 (v karteziánskej sústave kladná časť osi
(v karteziánskej sústave kladná časť osi  ), nazývame ju polárna os
), nazývame ju polárna os - Bod
 je definovaný usporiadanou dvojicou
je definovaný usporiadanou dvojicou 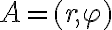 kde
kde 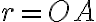 je vzdialenosť od pólu
je vzdialenosť od pólu  a
a 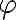 je orientovaný uhol medzi polárnou osou a polpriamkou
je orientovaný uhol medzi polárnou osou a polpriamkou 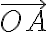 .
.
- Polárne súradnice môžu byť konvertované na karteziánske súradnice pomocou trigonometrických funkcií:
-
Karteziánske súradnice
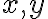 môžu byť premenené na polárne súradnice v intervale
môžu byť premenené na polárne súradnice v intervale 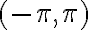 :
: ![r = \sqrt[]{x^2+y^2} r = \sqrt[]{x^2+y^2}](https://lms.umb.sk/filter/tex/pix.php/7b5208b981ae22accb9a6eabff9d9cca.png) ,
, 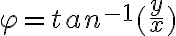
- Polárne súradnice sa vo veľkej miere používajú
- v navigácii, na modelovanie systémov, ktoré vykazujú radiálnu symetriu
- napr. pre prietok podzemnej vody alebo radiálnu silu ako gravitačné polia

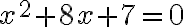
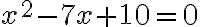
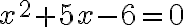
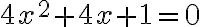
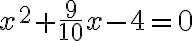
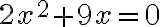
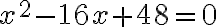
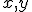
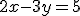
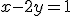
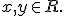
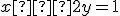

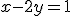
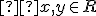
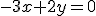
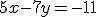
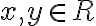
![\small [x; y] = [ ; ]. \small [x; y] = [ ; ].](https://lms.umb.sk/filter/tex/pix.php/16d67f80b591b0de370f5302200b8910.png)