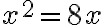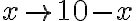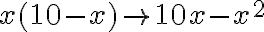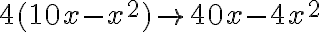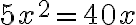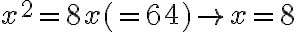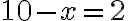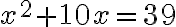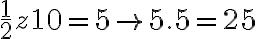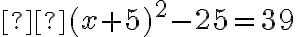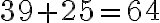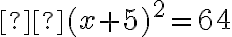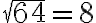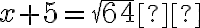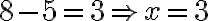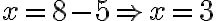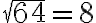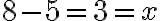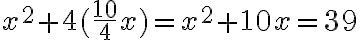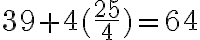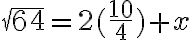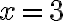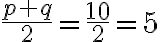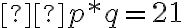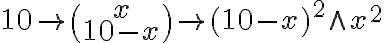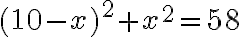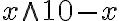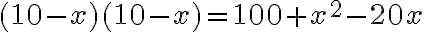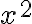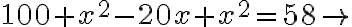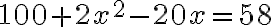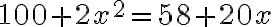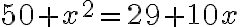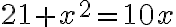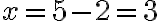Indo-arabská matematika
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Dejiny matematiky |
| Kniha: | Indo-arabská matematika |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:25 |
Grécky vplyv
- Šalvasutry (Pravidlá povrazca) – „meračstvo“ (7. až 5. storočí pred n. l.)
- Siddhánty (Učenosti), Arjábhattija - vznikli vo 4. - 5. stor. n. l.

Al-Chwárizmího aritmetická kniha bola preložená do latinčiny. Pôvodný arabský text sa nezachoval. Prepracovanejšia verzia prekladu s arabskými číslami sa do kresťanskej Európy dostala v 12. storočí.
Al-Chwárizmí
- Kniha o sčítaní a odčítaní podľa indického počtu (Kitáb al-dam wa-t-tafrígh bi-hisáb al-Hind)
- Krátka kniha o počte algebry a al-muqábaly (Al-kitáb al-muchtasar fí hisáb al-džabr wa-l-muqábala).
- V knihe sú objasnené číselné algoritmy pre aritmetické operácie v tejto sústave. Dochovala sa však len v latinskom preklade s názvom Libro algorismi de practica arismatrice (Algorizmova kniha o praxi aritmetiky) z polovice 12. storočia odkiaľ vzniklo slovo algoritmus.
- Jej prínos pre matematiku:
- Aritmetické operácie boli prevádzane v desiatkovej sústave.
- Prvé použitie nuly v zápise čísla bolo pravdepodobne v tejto práci.
- Prvá systematicky spracovaná práca o číselných sústavách.
- Al-Chwárizmi pri riešení kvadratických rovníc pracuje s objektmi: Mál, Káb, Džizr (jidhr), Šai, Dirhem.
- Mál môžeme interpretovať ako druhu mocninu neznámej:
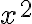 .
. - Káb ako tretiu mocninu neznámej:
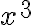 . Vyššie mocniny vytvára opakovaním: málmál
. Vyššie mocniny vytvára opakovaním: málmál
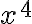 , kábmál...
, kábmál...
- Džizr
aj šai predstavuje premennú
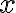 ako koreň rovnice.
ako koreň rovnice.
- Dirhem (dobová minca ) bol pojem pre náš absolútny člen rovnice. Bolo nim kladné prirodzené číslo, v niektorých prípadoch kladné racionálne číslo.
Jaromír Baštinec,Zdeňka Kubištová: Muhammad ibn Músa al-Chorezmi.Matematika v proměnách věků.I . Dostupné Tu.
Ukážky z traktátov
- štvorce
- korene
- jednoduché čísla, ktoré nie sú koreňové ani štvorcové.
Koreň je akékoľvek množstvo, ktoré sa má vynásobiť samo o sebe, skladajúce sa z jednotiek alebo čísel.
Štvorec je celé množstvo samotného koreňa."
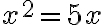 ], čo je to isté ako
], čo je to isté ako
„Štvorec je dvadsaťpäť“ [...
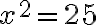 ] alebo
] alebo
„Koreň je päť“ [...
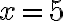 ] .
] .
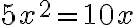 ]
]
„Jeden štvorec je rovný dvom koreňom“ [...
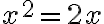 ]
]
„Štvorec je štyri“ [...
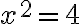 ]
]
„Koreň je dva“ [...
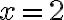 ].
].
-
Al-jabr predstavuje metódu eliminácie záporných členov rovnice. K obidvom stranám rovnice pričítame rovnaké členy.
Napríklad vyraz
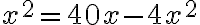 al-jabrou upravíme na tvar
al-jabrou upravíme na tvar 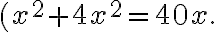
- Al-muqábala kladné členy s rovnakou mocninou sú redukované tak, že každý objekt (Māl, Džizr, Dirhem) sa nachádza maximálne raz.
Aplikovaním al-muqábaly:
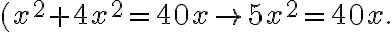
- Al-rad ak je koeficient pri najvyššej mocnine rôzny od jednotky, tak sa ním vydelí celá rovnica. Ak použijeme alrad:
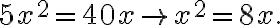
- Al-ikmal ak je koeficient pri najvyššej mocnine je zlomok
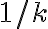 , tak sa celá rovnica násobí číslom
, tak sa celá rovnica násobí číslom  .
.
V Európe sa slovo algebra ako názov vedy objavuje v 14. storočí.
Kvadratické rovnice
„Zistili sme, že všetko potrebné pre uskutočnenie výpočtov al-gābry a al-muqābaly ťa privedie k jednej zo šiestich kapitol, vyložených a vysvetlených mnou v tejto knihe. Vedz to."
- Štvorec koreňom rovný (Substantiae radices coaequant):
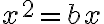
- Štvorec číslam rovný (Substantiae numeros coaequant):
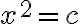
- Korene číslam rovné (Radices numeros coaequant):
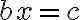
- Štvorec a korene číslam rovné (Substantia et radices numeros coaequant):
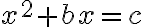
- Štvorec a čísla koreňom rovné (Substancia et numeri radices coaequant):
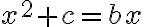
- Korene a čísla štvorcu rovné (Radices et numeri substantiam coaequant):
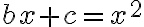
Prvý typ
- Zadanie: „Rozdelil si desať na dve časti, vynásobil si jednu z častí druhou a ďalej si vynásobil jednu z nich samu sebou.“
- Úloha: „Potom tento súčin sama so sebou sa stal rovným štvornásobku súčinu oboch časti".
- „Pravidlo je nasledujúce:
- „
Vezmi jednu z častí ako vec, potom druha je desať bez veci."
- „Vynásob vec krát desať bez veci, dostaneš desať vecí bez štvorca.“
- „Ďalej to násob štyrmi, ako ti bolo povedané: štyrikrát. Dostaneš štyri násobky jednej časti s druhou, to je štyridsať veci bez štyroch štvorcov.“
- „Potom násob vec vecou, to je jednu časť samu sebou. Dostaneš:štvorec je rovný štyridsiatim veciam bez štyroch štvorcov.“
- „Doplň to štyrmi štvorcami a pridaj ku štvorcu.Dostaneš: štyridsať veci je rovno piatim štvorcom.“
- „Preto je jeden štvorec rovný ôsmym koreňom, to je šesťdesiatštyri. Jeho koreň je osem. To je jedna z časti vynásobená sama sebou.“
- „Ostatok do desať je druha časť.
- Tato úloha ťa priviedla k jednému zo šiestich oddielov, menovite: štvorec rovný koreňom.“ (Al-Chwarizmi 2008, s. 134).
Štvrtý typ
- Úloha: „Štvorec a desať jeho koreňov je rovných tridsiatim deviatim dirhemom".
- „Pravidlo je nasledujúce:
- „Rozpoľ počet koreňov a získaš päť, násob to samo sebou a máš dvadsať päť"
- „Výsledok pridaj k tridsiatim deviatim a máš šesťdesiat štyri.“
- „Nájdi z toho koreň, máš osem a odčítaj polovicu koreňov, čo je päť a zostanú ti tri".
- „To je koreň štvorca, ktorý hľadáš, a štvorec je deväť.“
Piaty typ
- Zadanie: „Rozdelil som desať na dve časti, vynásobil som potom každú z nich samu sebou.“
- Úloha: „Keď som ich sčítal, súčet bol päťdesiat osem dirhemov".
- Výpočet
- Vezmi jednu z častí ako vec a druhu ako desať bez veci.
- Vynásob desať bez veci samu sebou, získaš sto a štvorec bez dvadsať veci.
- Potom vynásob vec samu sebou, to je štvorec.
- Všetko spolu sčítaj. Súčet je sto a dva štvorce bez dvadsiatich veci, ktoré sú rovne päťdesiatim ôsmim dirhemom.
- Vezmi teraz dvadsať záporných veci zo sto a dvoch štvorcov a pridaj ich k päťdesiatim ôsmim. Potom sto a dva štvorce sú rovne päťdesiatim ôsmim dirhemom a dvadsiatim veciam.
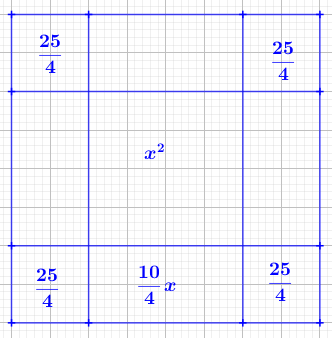
- Preveď to na jeden štvorec, teda medzi polovicu toho, čo máš. Získaš päťdesiat dirhemov a štvorec, ktoré sú rovné dvadsiatim deviatim dirhemom a desiatim veciam.
- Potom preveď to, odčítaním dvadsať deväť od päťdesiat. Zostane dvadsať jeden a štvorec, ktoré sú rovné desiatim veciam. Teraz Al-Chvarizmi využije "substitúciu": Nech sú korene rovnice
- Polovica čísla koreňov je päť a násobená sama sebou je dvadsaťpäť.
- Odober od toho dvadsaťjeden, ktoré sú spojene so štvorcom a zostatok sú štyri.
-
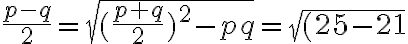
- Nájdi koreň, to je dva.
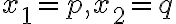 . Potom
. Potom
-
Al-Chvarizmi poznal vzťahy medzi koreňmi a koeficientami kvadratickej rovnice!
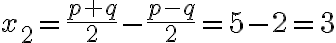 ,
, 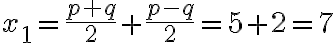
Záver
Al-Chvarizmí patrí medzi najvýznamnejších matematikov všetkých dôb. Dal meno celej jednej vetve matematiky - algebre.
Jeho meno je v latinizovanej forme súčasťou všetkých moderných jazykov ako slovo algoritmus.
Rozhodujúca je jeho propagácia indickej pozičnej desiatkovej sústavy a systematizácia postupov pre riešenie lineárnych a kvadratických rovníc.
V predslove k svojmu algebraickému traktátu píše, že sa snažil o zostavení príručky podľa potrieb praxe. Nejde teda o vedeckú prácu, ale o učebnicu. A to o veľmi dobrú učebnicu, ktorá slúžila svojmu účelu mnoho stoviek rokov. V knižnici v Drážďanoch je zachovaný prepis al-Chorezmiho algebry zo 14. storočia.
V úvode k svojmu algebraickému spisu al-Chvarizmí píše:
Kým jednej časti učencov náleží priorita objavu, objasňuje druhá skupina obtiažna miesta v prácach svojich predchodcov a tým uľahčuje ich pochopenie. Iní učenci sa potom zaoberajú systematizováním už existujúcich vedomostí, pričom opravujú nepresnosti a zdokonaľujú myšlienky svojich spolupracovníkov. A to všetko "bez pýchy a hrdosti v duši".
Úlohy
Vypracujte seminárnu prácu na tému "V čom ma zaujala Indo-arabská matematika".
Použite literatúru "Aritmetický a algebraický traktát Al Chvárizmí".

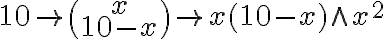
![x^2=4[x(10-x)] x^2=4[x(10-x)]](https://lms.umb.sk/filter/tex/pix.php/f6507a94fe1a26cd764dbda1ae2f9c9b.png)