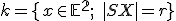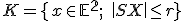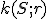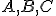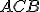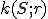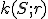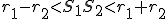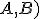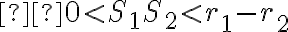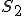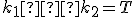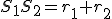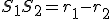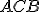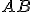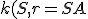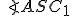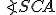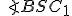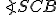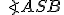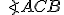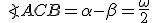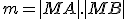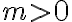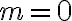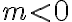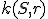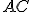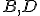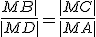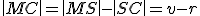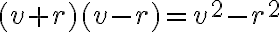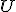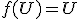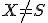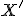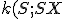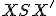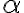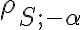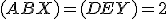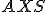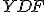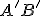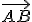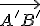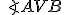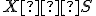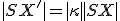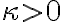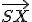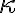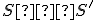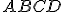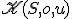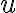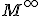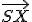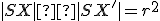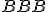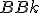Geometria kružnice
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria N |
| Kniha: | Geometria kružnice |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 10:25 |
Kružnica, kruh
Definícia.
Množina všetkých bodov v rovine, ktoré majú od pevného bodu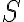 vzdialenosť rovnú kladnému reálnemu číslu
vzdialenosť rovnú kladnému reálnemu číslu 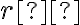 sa nazýva kružnica so stredom
sa nazýva kružnica so stredom  a polomerom
a polomerom  . Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu  vzdialenosť menšiu alebo rovnú číslu
vzdialenosť menšiu alebo rovnú číslu  sa nazýva kruh so stredom
sa nazýva kruh so stredom  a polomerom
a polomerom  . Symbolicky
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
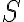 vzdialenosť rovnú kladnému reálnemu číslu
vzdialenosť rovnú kladnému reálnemu číslu 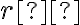 sa nazýva kružnica so stredom
sa nazýva kružnica so stredom  a polomerom
a polomerom  . Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu  vzdialenosť menšiu alebo rovnú číslu
vzdialenosť menšiu alebo rovnú číslu  sa nazýva kruh so stredom
sa nazýva kruh so stredom  a polomerom
a polomerom  . Symbolicky
. Symbolicky
Bod
 nazývame stred kružnice resp. stred kruhu a číslo
nazývame stred kružnice resp. stred kruhu a číslo 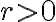 polomer kružnice resp. kruhu.
polomer kružnice resp. kruhu.
Ľubovoľné dva body kružnice delia túto kružnicu na dve časti, ktoré nazývame oblúky kružnice alebo kružnicové oblúky.
Dva polomery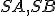 rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
Tetiva rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
 nazývame stred kružnice resp. stred kruhu a číslo
nazývame stred kružnice resp. stred kruhu a číslo 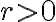 polomer kružnice resp. kruhu.
polomer kružnice resp. kruhu.
Ľubovoľné dva body kružnice delia túto kružnicu na dve časti, ktoré nazývame oblúky kružnice alebo kružnicové oblúky.
Dva polomery
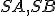 rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
Tetiva
 rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
Definícia.
V geometrii skúmame vlastnosti geometrických útvarov v dvoch základných kategóriách, ktoré zahŕňajú:
- polohové vlastnosti,
- metrické vlastnosti.
- vzájomnú polohu priamky a kružnice,
- vzájomnú polohu dvoch kružníc.
- vzťah medzi veľkosťou stredového uhla a prislúchajúcich obvodových uhloch v kružnici,
- mocnosť bodu ku kružnici.
Je daná kružnica 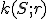 a priamka
a priamka 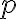 . Nech
. Nech 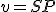 je vzdialenosť priamky od stredu kružnice
je vzdialenosť priamky od stredu kružnice 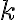 .
.
Môžu nastať len tri prípady: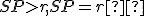 alebo
alebo 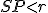 .
Aktivujte zaškrtávacie políčko v applete.
.
Aktivujte zaškrtávacie políčko v applete.
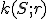 a priamka
a priamka 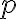 . Nech
. Nech 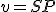 je vzdialenosť priamky od stredu kružnice
je vzdialenosť priamky od stredu kružnice 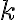 .
.
Môžu nastať len tri prípady:
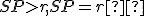 alebo
alebo 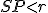 .
Aktivujte zaškrtávacie políčko v applete.
.
Aktivujte zaškrtávacie políčko v applete.
-
Ak má priamka
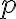 od stredu
od stredu 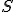 kružnice
kružnice 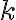 vzdialenosť
vzdialenosť 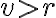 , tak priamka
, tak priamka 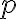 kružnicu
kružnicu 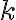 nepretína.
nepretína. -
Ak priamka má od stredu kružnice vzdialenosť rovnú polomeru
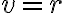 , tak má priamka s kružnicou jediný spoločný bod
, tak má priamka s kružnicou jediný spoločný bod 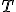 .
. - Priamka, ktorá má s kružnicou jediný spoločný bod, sa nazýva dotyčnica kružnice.
- Spoločný bod priamky a kružnice je bod dotyku.
- Dotyčnica je vždy kolmá na polomer kružnice
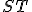 .
.
-
Ak má priamka od stredu kružnice vzdialenosť
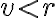 , tak má priamka a kružnica dva rôzne spoločné body.
, tak má priamka a kružnica dva rôzne spoločné body. - Priamka, ktorá má s kružnicou dva rôzne spoločné body, sa nazýva sečnica kružnice.
- Spoločné body priamky a kružnice sú ich priesečníky.
Definícia.
Dané dve kružnice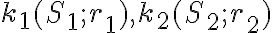 s rôznymi stredmi. Priamka (resp. úsečka)
s rôznymi stredmi. Priamka (resp. úsečka) 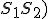 )
sa nazýva stredná týchto dvoch kružníc.
)
sa nazýva stredná týchto dvoch kružníc.
Dané dve kružnice
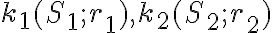 s rôznymi stredmi. Priamka (resp. úsečka)
s rôznymi stredmi. Priamka (resp. úsečka) 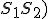 )
sa nazýva stredná týchto dvoch kružníc.
)
sa nazýva stredná týchto dvoch kružníc.
Veta o obvodových uholch
Veta (O obvodových uhloch).
Ľubovoľné dva obvodové uhly prislúchajúce k tomu istému oblúku kružnice majú rovnakú veľkosť.
Obvodový uhol je polovicou stredového uhla prislúchajúceho k tomu istému oblúku.
Ľubovoľné dva obvodové uhly prislúchajúce k tomu istému oblúku kružnice majú rovnakú veľkosť.
Obvodový uhol je polovicou stredového uhla prislúchajúceho k tomu istému oblúku.
-
Priložený applet je motivačný a môžete ho využiť pri skúmaní závislosti veľkosti obvodových uhlov
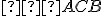 od polohy bodu
od polohy bodu 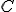 .
. -
Veľkosť obvodového uhla nezávisí od polohy bodu
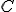 , rozhodujúce sú body
, rozhodujúce sú body 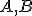 resp. uhol
resp. uhol 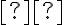 .
. - Konštrukcia oblúka, z ktorého vidieť úsečku pod daným uhlom. Otvorte si konštrukciu Tu.
- Ak body
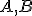 sú krajné body priemeru, tak rozdelia kružnicu na dve polkružnice: stredový uhol je priamy a obvodový uhol pravý.
sú krajné body priemeru, tak rozdelia kružnicu na dve polkružnice: stredový uhol je priamy a obvodový uhol pravý.
Dôkaz (vety o obvodových uhloch).
V dôkaze vety o obvodových uhloch sa využívajú dve základné vlastnosti trojuholníka.
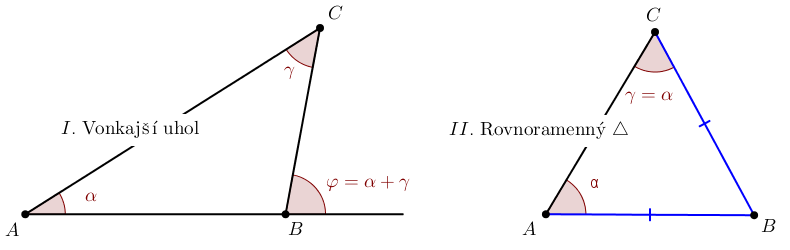
Spojením týchto dvoch tvrdení dostaneme:
V dôkaze vety o obvodových uhloch sa využívajú dve základné vlastnosti trojuholníka.
- "Vonkajší uhol trojuholníka sa rovná súčtu vnútorných uhlov pri zvyšných vrcholoch."
- "V rovnoramennom trojuholníku sa uhly pri základni navzájom rovnajú" (Kniha 1, Tvrdenie V).
Spojením týchto dvoch tvrdení dostaneme:
Dôsledok.
Prípad 1 (Veta o obvodových uhloch).
Nech je vnútorný bod uhla
je vnútorný bod uhla 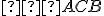 . Potom obvodový uhol
. Potom obvodový uhol 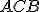 je polovicou stredového
uhla
je polovicou stredového
uhla 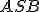 .
.
Nech
 je vnútorný bod uhla
je vnútorný bod uhla 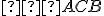 . Potom obvodový uhol
. Potom obvodový uhol 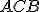 je polovicou stredového
uhla
je polovicou stredového
uhla 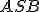 .
.
Prípad 2 (Veta o obvodových uhloch).
Nech leží na ramene uhla
leží na ramene uhla 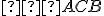 Potom obvodový uhol
Potom obvodový uhol 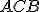 je tiež polovicou stredového uhla
je tiež polovicou stredového uhla 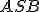 .
.
Nech
 leží na ramene uhla
leží na ramene uhla 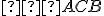 Potom obvodový uhol
Potom obvodový uhol 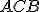 je tiež polovicou stredového uhla
je tiež polovicou stredového uhla 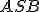 .
.
Posuňte bod C proti smeru hodinových ručičiek do krajnej polohy vľavo tak, aby body 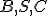 ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
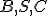 ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
Prípad 3 (Veta o obvodových uhloch).
Nech S je vonkajší bod uhla ∡ACB. Potom obvodový uhol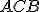 je polovicou stredového uhla
je polovicou stredového uhla 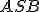 .
.
Nech S je vonkajší bod uhla ∡ACB. Potom obvodový uhol
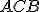 je polovicou stredového uhla
je polovicou stredového uhla 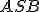 .
.
Zrejme platí 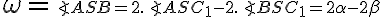 . Pozrime sa na rozdiel uhlov pri vrchole
. Pozrime sa na rozdiel uhlov pri vrchole 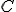 .
Zistíme, že
.
Zistíme, že 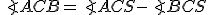 . Keďže trojuholníky
. Keďže trojuholníky 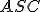 ,
, 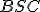 sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod
sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod 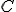 môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
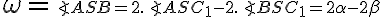 . Pozrime sa na rozdiel uhlov pri vrchole
. Pozrime sa na rozdiel uhlov pri vrchole 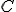 .
Zistíme, že
.
Zistíme, že 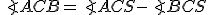 . Keďže trojuholníky
. Keďže trojuholníky 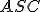 ,
, 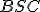 sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod
sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod 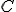 môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
Príklad.
Je daná kružnica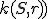 a na nej dva body
a na nej dva body 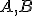 . Pre každý priemer
. Pre každý priemer
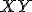 kružnice
kružnice  zostrojíme (ak existuje) priesečník priamok
zostrojíme (ak existuje) priesečník priamok 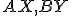 .
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že
.
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že 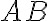 nie je priemer kružnice. (Larson 8.1.2. - zadanie Tu.)
nie je priemer kružnice. (Larson 8.1.2. - zadanie Tu.)
Je daná kružnica
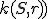 a na nej dva body
a na nej dva body 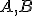 . Pre každý priemer
. Pre každý priemer
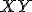 kružnice
kružnice  zostrojíme (ak existuje) priesečník priamok
zostrojíme (ak existuje) priesečník priamok 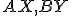 .
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že
.
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že 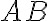 nie je priemer kružnice. (Larson 8.1.2. - zadanie Tu.)
nie je priemer kružnice. (Larson 8.1.2. - zadanie Tu.)
V planimetrii sa pomerne často vyskytujú úlohy, v ktorých sa hľadá množina  bodov s danou vlastnosťou
bodov s danou vlastnosťou 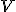 .
Symolicky to môžeme zapísať takto
.
Symolicky to môžeme zapísať takto 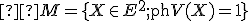 . Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
. Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
 je kružnicový oblúk
je kružnicový oblúk 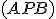 . Na overenie platnosti výroku "
. Na overenie platnosti výroku "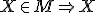 má vlastnosť
má vlastnosť 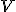 " teraz stačí ukázať, že výroková formula
" teraz stačí ukázať, že výroková formula ![[(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.) [(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.)](https://lms.umb.sk/filter/tex/pix.php/1d2466a43806dc0ae93b0078ee6c0d9a.png) je tautológia. To je však zrejmé. Keďže aj opačný postup
je tautológia. To je však zrejmé. Keďže aj opačný postup ![[(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1. [(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1.](https://lms.umb.sk/filter/tex/pix.php/af5824de788b473b6bd4ab77ebe529d5.png) je tautológia, tak aj časť C je pravdivý výrok.
je tautológia, tak aj časť C je pravdivý výrok.
 bodov s danou vlastnosťou
bodov s danou vlastnosťou 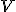 .
Symolicky to môžeme zapísať takto
.
Symolicky to môžeme zapísať takto 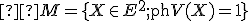 . Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
. Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
- Najskôr musíme určiť základné charakteristické prvky danej množiny (najčastejšie experimentálne) resp. komplexne popísať danú množinu
 .
Potom overiť platnosť výrokov:
.
Potom overiť platnosť výrokov: 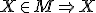 má vlastnosť
má vlastnosť 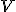 ,
, - ak
 má vlastnosť
má vlastnosť 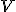 , tak patrí do množiny
, tak patrí do množiny  .
.
- Thalesova veta hovorí, že trojuholníky
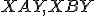 sú pravouhlé s pravým uhlom pri vrcholoch
sú pravouhlé s pravým uhlom pri vrcholoch 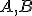 .
. - Obvodové uhly
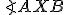 a
a 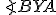 majú rovnakú veľkosť
majú rovnakú veľkosť  .
. - Označme si
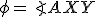 a
a 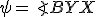 .
. - Súčet uhlov v trojuholníku je 180°, preto
bude
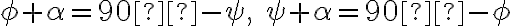 .
. - Odtiaľ dostávame, že súčet uhlov
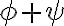 je konštantný pre ľubovoľný priemer
je konštantný pre ľubovoľný priemer 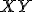 a dva pevné body
a dva pevné body 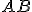 .
. - Preto aj vrcholové uhly
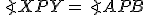 majú konštantnú veľkosť. To znamená, že body
majú konštantnú veľkosť. To znamená, že body 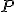 ležia na kružnicovom oblúku
ležia na kružnicovom oblúku
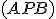 .
. - K nájdeniu oblúka stačí zvoliť jeden priemer
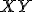 a jeden odpovedajúci priesečník
a jeden odpovedajúci priesečník 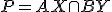 .
.
 je kružnicový oblúk
je kružnicový oblúk 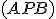 . Na overenie platnosti výroku "
. Na overenie platnosti výroku "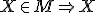 má vlastnosť
má vlastnosť 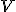 " teraz stačí ukázať, že výroková formula
" teraz stačí ukázať, že výroková formula ![[(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.) [(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.)](https://lms.umb.sk/filter/tex/pix.php/1d2466a43806dc0ae93b0078ee6c0d9a.png) je tautológia. To je však zrejmé. Keďže aj opačný postup
je tautológia. To je však zrejmé. Keďže aj opačný postup ![[(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1. [(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1.](https://lms.umb.sk/filter/tex/pix.php/af5824de788b473b6bd4ab77ebe529d5.png) je tautológia, tak aj časť C je pravdivý výrok.
je tautológia, tak aj časť C je pravdivý výrok.
Poznámky.
- Pri určovaní GMB je mnohokrát najťažší krok A.
- Program GeoGebra tento krok zjednoduší tým, že pomocou nástroja "Množina bodov" (nachádza sa v sekcii nástrojov "Kolmica") vykreslí hľadanú
množinu
 .
. - Potom je však nutné realizovať kroky B a C.
- Pozrite si aplikovanie tohto nástroja v kurze Didaktika matematiky v knihe Množiny bodov. Dostupné Tu.
Mocnosť bodu ku kružnici
Je daná kružnica 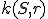 so stredom
so stredom  a polomerom
a polomerom 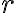 . Bod
. Bod  leží zvonka kružnice. Nech
leží zvonka kružnice. Nech 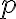 je sečnica
kružnice
je sečnica
kružnice 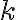 vedená bodom
vedená bodom  a
a  sú priesečníky sečnice s kružnicou
sú priesečníky sečnice s kružnicou 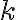 .
.
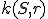 so stredom
so stredom  a polomerom
a polomerom 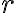 . Bod
. Bod  leží zvonka kružnice. Nech
leží zvonka kružnice. Nech 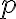 je sečnica
kružnice
je sečnica
kružnice 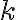 vedená bodom
vedená bodom  a
a  sú priesečníky sečnice s kružnicou
sú priesečníky sečnice s kružnicou 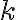 .
.
Skúmajme súčin 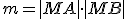 . Po otvorení motivačného appletu a experimentovaním s polohou bodu
. Po otvorení motivačného appletu a experimentovaním s polohou bodu  , môžeme vysloviť hypotézu:
, môžeme vysloviť hypotézu:
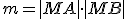 . Po otvorení motivačného appletu a experimentovaním s polohou bodu
. Po otvorení motivačného appletu a experimentovaním s polohou bodu  , môžeme vysloviť hypotézu:
, môžeme vysloviť hypotézu:
Otázky.
Je súčin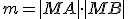 nezávislý od polohy sečnice
nezávislý od polohy sečnice 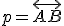 ? Inými slovami je konštantný pre ľubovoľnú polohu bodov
? Inými slovami je konštantný pre ľubovoľnú polohu bodov  ?
?
Môžeme definovať súčin aj pre prípad, ak bod leží vo vnútri kružnice
leží vo vnútri kružnice 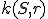 ? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
Je súčin
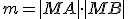 nezávislý od polohy sečnice
nezávislý od polohy sečnice 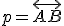 ? Inými slovami je konštantný pre ľubovoľnú polohu bodov
? Inými slovami je konštantný pre ľubovoľnú polohu bodov  ?
?
Môžeme definovať súčin aj pre prípad, ak bod
 leží vo vnútri kružnice
leží vo vnútri kružnice 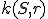 ? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
Definícia (Mocnosť bodu ku kružnici).
Ľubovoľnému bodu roviny možno priradiť reálne číslo
roviny možno priradiť reálne číslo 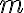 , pre ktorého absolútnu hodnotu platí
, pre ktorého absolútnu hodnotu platí 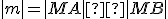 , pričom
, pričom
Ľubovoľnému bodu
 roviny možno priradiť reálne číslo
roviny možno priradiť reálne číslo 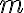 , pre ktorého absolútnu hodnotu platí
, pre ktorého absolútnu hodnotu platí 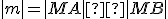 , pričom
, pričom
Dôkaz.
Dokázať tento dôsledok je veľmi jednoduché. Stačí zvoliť sečnicu 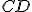 tak, aby prechádzala stredom kružnice. V takom prípade bude
tak, aby prechádzala stredom kružnice. V takom prípade bude
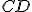 tak, aby prechádzala stredom kružnice. V takom prípade bude
tak, aby prechádzala stredom kružnice. V takom prípade bude
Poznámka.
V prípade, keď bod leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky
leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky 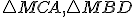 sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo
sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo 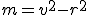 záporné. Pozrite si ilustračný obrázok.
záporné. Pozrite si ilustračný obrázok.
V prípade, keď bod
 leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky
leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky 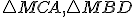 sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo
sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo 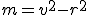 záporné. Pozrite si ilustračný obrázok.
záporné. Pozrite si ilustračný obrázok.
Nasledujúca veta platí len v prípade, že bod
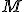 je mimo kružnice
je mimo kružnice  . Mocnosť bodu
. Mocnosť bodu 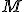 v tomto prípade môžeme vyjadriť
pomocou veľkosti úsečky
v tomto prípade môžeme vyjadriť
pomocou veľkosti úsečky 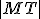 , kde
, kde 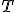 je dotykový bod dotyčnice ku kružnici, ktorá prechádza bodom
je dotykový bod dotyčnice ku kružnici, ktorá prechádza bodom 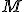 .
.
Veta 2.
Pre mocnosť bodu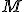 , ktorý leží zvonka kružnice
, ktorý leží zvonka kružnice 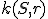 , platí rovnosť
, platí rovnosť 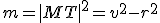 . Bod
. Bod 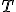 je dotykový bod dotyčnice, ktorá prechádza bodom
je dotykový bod dotyčnice, ktorá prechádza bodom  .
.
Pre mocnosť bodu
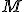 , ktorý leží zvonka kružnice
, ktorý leží zvonka kružnice 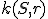 , platí rovnosť
, platí rovnosť 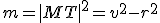 . Bod
. Bod 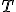 je dotykový bod dotyčnice, ktorá prechádza bodom
je dotykový bod dotyčnice, ktorá prechádza bodom  .
.
Dôkaz vety 2 ilustrujeme ako limitný prechod vo veta 1.
 Pomocou obrázka urobte korektný matematický dôkaz. Využite podobnosť trojuholníkov
Pomocou obrázka urobte korektný matematický dôkaz. Využite podobnosť trojuholníkov 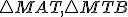 , ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí
, ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí 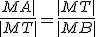 .
.
Pri odvodení vzťahu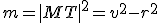 môžeme využiť skutočnosť, že trojuholník
môžeme využiť skutočnosť, že trojuholník 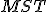 je pravouhlý a použiť Pytagorovu vetu.
je pravouhlý a použiť Pytagorovu vetu.
- Vzťah
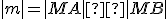 platí pro ľubovoľnú sečnicu.
platí pro ľubovoľnú sečnicu. - Pohybujme sečnicou tak, aby sa postupne blížila k dotyčnici v bode
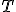 .
. - Bod
 i bod
i bod 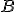 sa blížia k bodu
sa blížia k bodu 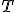 .
. - Veľkosť úsečky
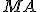 sa blíži k veľkosti úsečky
sa blíži k veľkosti úsečky 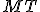 .
. - Z toho usudzujeme, že súčin
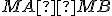 sa blíži k súčinu
sa blíži k súčinu 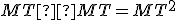 .
.

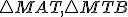 , ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí
, ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí 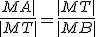 .
.
Pri odvodení vzťahu
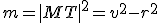 môžeme využiť skutočnosť, že trojuholník
môžeme využiť skutočnosť, že trojuholník 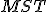 je pravouhlý a použiť Pytagorovu vetu.
je pravouhlý a použiť Pytagorovu vetu.
Definícia (Chordála a chordický bod).
Majme dve nesústredné kružnice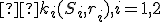 . Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
. Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
Majme dve nesústredné kružnice
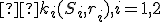 . Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
. Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
Korektnosť definície a konštrukcia chordály.
- Dané kružnice
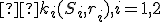 sa pretínajú v dvoch bodoch/priesečníkoch. Priamka určená priesečníkmi daných kružníc je spoločná sečnica oboch kružníc. Preto ľubovoľný bod priamky určenej týmito priesečníkmi má rovnakú mocnosť k obom kružniciam. Priamka určená priesečníkmi daných kružníc je chordála daných kružníc.
sa pretínajú v dvoch bodoch/priesečníkoch. Priamka určená priesečníkmi daných kružníc je spoločná sečnica oboch kružníc. Preto ľubovoľný bod priamky určenej týmito priesečníkmi má rovnakú mocnosť k obom kružniciam. Priamka určená priesečníkmi daných kružníc je chordála daných kružníc. - Kružnice sa dotýkajú v bode, ktorý má mocnosť
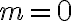 k obom kružniciam. Chordála je spoločná dotyčnica v bode. Dôkaz, že spoločná dotyčnica je množina bodov s rovnakou mocnosťou k obom kružniciam, vyplýva z vety 2.
k obom kružniciam. Chordála je spoločná dotyčnica v bode. Dôkaz, že spoločná dotyčnica je množina bodov s rovnakou mocnosťou k obom kružniciam, vyplýva z vety 2. - V prípade, že kružnice nemajú spoločný bod zvoľme pomocnú kružnicu
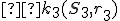 , ktorá pretína obe kružnice
, ktorá pretína obe kružnice 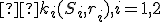 . Zostrojme chordály
. Zostrojme chordály 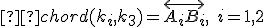 . Ich priesečník označme
. Ich priesečník označme 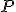 . Tento bod má rovnakú mocnosť ku všetkým trom kružniciam. Nazývame ho chordický bod. Týmto bodom potom vedieme kolmicu k úsečke, čo je chordála kružníc
. Tento bod má rovnakú mocnosť ku všetkým trom kružniciam. Nazývame ho chordický bod. Týmto bodom potom vedieme kolmicu k úsečke, čo je chordála kružníc 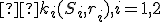 . Aktivujte si priložený applet.
. Aktivujte si priložený applet.
Cvičenie II
- Zostrojte trojuholník
 , pre ktorý sú dané ťažnice
, pre ktorý sú dané ťažnice 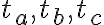 .
. -
Zostrojte trojuholník
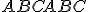 , pre ktorý je dané:
, pre ktorý je dané: 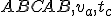 . Riešenie vyhľadajte v práci [DAV].
. Riešenie vyhľadajte v práci [DAV].
-
Zostrojte trojuholník
 , pre ktorý je daná výška
, pre ktorý je daná výška 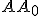 , ťažnica
, ťažnica 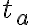 a stred opísanej kružnice
a stred opísanej kružnice  . Zadanie Tu. Riešenie Tu.
. Zadanie Tu. Riešenie Tu. -
Daná je úsečka
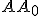 a priamka
a priamka  . Zostrojte trojuholník
. Zostrojte trojuholník  s vrcholom
s vrcholom  a výškou
a výškou
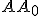 , ktorého ťažisko a stred kružnice opísanej ležia na priamke
, ktorého ťažisko a stred kružnice opísanej ležia na priamke  . Pozri 56. ročník MO, šk. rok 2006/2007, úloha B – I – 6. Riešenie Tu.
. Pozri 56. ročník MO, šk. rok 2006/2007, úloha B – I – 6. Riešenie Tu. -
Zostrojte trojuholník
 , pre ktorý je daná výška
, pre ktorý je daná výška 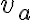 a ťažnice
a ťažnice 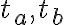 .
. - Zostrojte trojuholník
 , pre ktorý sú dané výšky
, pre ktorý sú dané výšky 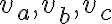 .
. -
Dokážte, že pre ťažnice
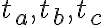 platí vzťah:
platí vzťah: 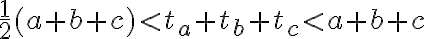 .Pozri prácu [KRI], str. 19.
.Pozri prácu [KRI], str. 19.
- Dokážte, že ťažnice v ľubovoľnom trojuholníku sa pretínajú v jednom bode pomocou osovej afinity.
Zobrazenia
Definícia.
Pod geometrickým zobrazením v rovine rozumieme predpis
rozumieme predpis 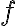 , ktorý ľubovoľnému bodu
, ktorý ľubovoľnému bodu 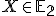 priradí najviac jeden bod
priradí najviac jeden bod 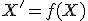 .
.
Pod geometrickým zobrazením v rovine
 rozumieme predpis
rozumieme predpis 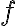 , ktorý ľubovoľnému bodu
, ktorý ľubovoľnému bodu 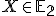 priradí najviac jeden bod
priradí najviac jeden bod 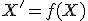 .
.
V tejto kapitole sa budeme skúmať
- zhodné a podobné zobrazenia,
- osovú afinitu,
- stredovú kolineáciu,
- kruhovú inverziu.
Definícia.
Zobrazenie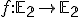 nazývame zhodné zobrazenie v (
nazývame zhodné zobrazenie v ( 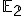 ), ak pre každé dva rôzne
body
), ak pre každé dva rôzne
body 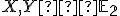 platí
platí
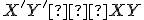 ,
,
kde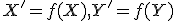 . Zhodné zobrazenia predstavujú geometrické zobrazenia euklidovskej roviny, ktoré zachovávajú incidenciu útvarov a vzdialenosť bodov (metriku).
. Zhodné zobrazenia predstavujú geometrické zobrazenia euklidovskej roviny, ktoré zachovávajú incidenciu útvarov a vzdialenosť bodov (metriku).
Zobrazenie
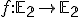 nazývame zhodné zobrazenie v (
nazývame zhodné zobrazenie v ( 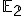 ), ak pre každé dva rôzne
body
), ak pre každé dva rôzne
body 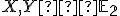 platí
platí
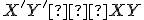 ,
,
kde
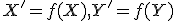 . Zhodné zobrazenia predstavujú geometrické zobrazenia euklidovskej roviny, ktoré zachovávajú incidenciu útvarov a vzdialenosť bodov (metriku).
. Zhodné zobrazenia predstavujú geometrické zobrazenia euklidovskej roviny, ktoré zachovávajú incidenciu útvarov a vzdialenosť bodov (metriku).
Rovinné geometrické útvary 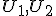 sa nazývajú zhodné , ak existuje zhodné zobrazenie, ktoré jeden z nich zobrazí na druhý. Zhodnosť dvoch útvarov symbolicky označíme takto:
sa nazývajú zhodné , ak existuje zhodné zobrazenie, ktoré jeden z nich zobrazí na druhý. Zhodnosť dvoch útvarov symbolicky označíme takto: 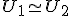 alebo takto
alebo takto 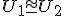 .
.
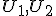 sa nazývajú zhodné , ak existuje zhodné zobrazenie, ktoré jeden z nich zobrazí na druhý. Zhodnosť dvoch útvarov symbolicky označíme takto:
sa nazývajú zhodné , ak existuje zhodné zobrazenie, ktoré jeden z nich zobrazí na druhý. Zhodnosť dvoch útvarov symbolicky označíme takto: 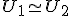 alebo takto
alebo takto 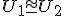 .
.
Definícia.
V euklidovskej rovine poznáme šesť typov zhodných zobrazení a to
- identitu,
- osovú súmernosť,
- stredovú súmernosť,
- otočenie (rotáciu),
- posunutie (transláciu),
- posunutú súmernosť.
Tvrdenie.
Zložením dvoch zhodných zobrazení je zhodné zobrazenie.
Zložením dvoch zhodných zobrazení je zhodné zobrazenie.
Dôkaz tohto tvrdenia prenechávame na čitateľa.
Definícia.
Nech je daná priamka. Zobrazenie, pre ktoré platí:
je daná priamka. Zobrazenie, pre ktoré platí:
Nech
 je daná priamka. Zobrazenie, pre ktoré platí:
je daná priamka. Zobrazenie, pre ktoré platí:
- obrazom bodu
 ležiaceho na priamke
ležiaceho na priamke 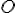 je bod
je bod 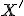 , ktorý je totožný s bodom
, ktorý je totožný s bodom  ,
, - obrazom bodu
 neležiaceho na priamke
neležiaceho na priamke 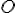 je bod
je bod 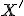 , pre ktorý platí, že priamka
, pre ktorý platí, že priamka 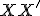 je kolmá na priamku
je kolmá na priamku
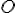 a stred úsečky
a stred úsečky 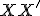 leží na priamke
leží na priamke 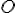 ,
,
nazývame osová súmernosť, - Priamku
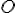 nazývame os osovej súmernosti. Osovú súmernosť s osou
nazývame os osovej súmernosti. Osovú súmernosť s osou 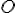 budeme označovať symbolom
budeme označovať symbolom 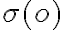 .
.
Cvičenie.
Je daná priamka a body
a body 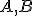 ležiace v tej istej polrovine s hraničnou priamkou
ležiace v tej istej polrovine s hraničnou priamkou  . Určte bod
. Určte bod 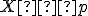 tak, aby súčet
tak, aby súčet
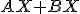 bol čo najmenší.
bol čo najmenší.
Riešenie Tu.
Je daná priamka
 a body
a body 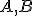 ležiace v tej istej polrovine s hraničnou priamkou
ležiace v tej istej polrovine s hraničnou priamkou  . Určte bod
. Určte bod 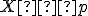 tak, aby súčet
tak, aby súčet
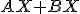 bol čo najmenší.
bol čo najmenší.
Riešenie Tu.
Stredová súmernosť a rotácia
Definícia.
Nech je daný bod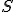 , uhol
, uhol 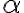 (veľkosť uhla je nanajvýš 360°) a orientácia kladná (proti smeru hodinových ručičiek)
resp. záporná (v smeru hodinových ručičiek). Zobrazenie, pre ktoré platí:
(veľkosť uhla je nanajvýš 360°) a orientácia kladná (proti smeru hodinových ručičiek)
resp. záporná (v smeru hodinových ručičiek). Zobrazenie, pre ktoré platí:
Nech je daný bod
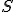 , uhol
, uhol 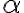 (veľkosť uhla je nanajvýš 360°) a orientácia kladná (proti smeru hodinových ručičiek)
resp. záporná (v smeru hodinových ručičiek). Zobrazenie, pre ktoré platí:
(veľkosť uhla je nanajvýš 360°) a orientácia kladná (proti smeru hodinových ručičiek)
resp. záporná (v smeru hodinových ručičiek). Zobrazenie, pre ktoré platí:
Tvrdenia (Rozklad zhodností na osové súmernosti).
- Identitu možno rozložiť na dve osové súmernosti, ktorých osi sú totožné. (Dôkaz prenechávame na čitateľa).
- Každú stredovú súmernosť možno rozložiť na dve osové súmernosti, ktorých osi sú na seba kolmé a prechádzajú stredom stredovej súmernosti.
- Každú rotáciu možno rozložiť na dve osové súmernosti, ktorých osi prechádzajú stredom rotácie, zvierajú uhol, ktorého veľkosť sa rovná jednej polovici veľkosti uhla rotácie, pričom orientácia uhla rotácie je súhlasná s orientáciou uhla od osi prvej osovej súmernosti ku osi druhej osovej súmernosti podľa poradia v zložení.
Cvičenie (Stredová súmernosť).
Sú dané dve sústredné kružnice a bod
a bod  vo vnútri
vo vnútri  . Zostrojte obdĺžnik
. Zostrojte obdĺžnik
 tak, že
tak, že 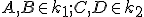 a bod
a bod  je jeho stredom.
Riešenie Tu.
je jeho stredom.
Riešenie Tu.
Sú dané dve sústredné kružnice
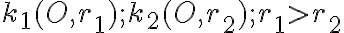 a bod
a bod  vo vnútri
vo vnútri 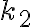 . Zostrojte obdĺžnik
. Zostrojte obdĺžnik
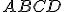 tak, že
tak, že 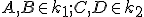 a bod
a bod  je jeho stredom.
Riešenie Tu.
je jeho stredom.
Riešenie Tu.Posunutie
Definícia.
Daný je vektor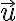 . Zobrazenie, pre ktoré platí, že obrazom bodu
. Zobrazenie, pre ktoré platí, že obrazom bodu  je bod
je bod 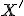 , pričom platí rovnosť vektorov
, pričom platí rovnosť vektorov
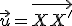 , sa nazýva posunutie alebo translácia.
, sa nazýva posunutie alebo translácia.
Vektor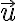 nazývame vektor posunutia. Posunutie o vektor
nazývame vektor posunutia. Posunutie o vektor 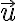 budeme označovať
budeme označovať 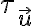 .
.
Daný je vektor
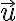 . Zobrazenie, pre ktoré platí, že obrazom bodu
. Zobrazenie, pre ktoré platí, že obrazom bodu  je bod
je bod 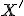 , pričom platí rovnosť vektorov
, pričom platí rovnosť vektorov
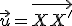 , sa nazýva posunutie alebo translácia.
, sa nazýva posunutie alebo translácia.
Vektor
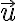 nazývame vektor posunutia. Posunutie o vektor
nazývame vektor posunutia. Posunutie o vektor 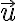 budeme označovať
budeme označovať 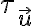 .
.
Tvrdenie.
Každé posunutie možno rozložiť na dve osové súmernosti, ktorých osi sú rovnobežné (rôzne), zároveň sú kolmé na vektor posunutia, ich vzdialenosť je rovná jednej polovici veľkosti vektora posunutia, pričom orientácia vektora posunutia je súhlasná s orientáciou od osi prvej osovej súmernosti ku osi druhej osovej súmernosti podľa poradia v zložení.
Každé posunutie možno rozložiť na dve osové súmernosti, ktorých osi sú rovnobežné (rôzne), zároveň sú kolmé na vektor posunutia, ich vzdialenosť je rovná jednej polovici veľkosti vektora posunutia, pričom orientácia vektora posunutia je súhlasná s orientáciou od osi prvej osovej súmernosti ku osi druhej osovej súmernosti podľa poradia v zložení.
Určenie vektora posunutia, ak posunutie je dané dvomi osovými súmernosťami je prezentované appletom "Posunutie".
Definícia.
Zostrojte rovnobežník ak sú dané veľkosti jeho strán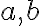 a veľkosť
a veľkosť 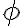 uhla, ktorý zvierajú jeho uhlopriečky.
uhla, ktorý zvierajú jeho uhlopriečky.
Zostrojte rovnobežník ak sú dané veľkosti jeho strán
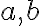 a veľkosť
a veľkosť 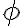 uhla, ktorý zvierajú jeho uhlopriečky.
uhla, ktorý zvierajú jeho uhlopriečky.
Definícia.
Zobrazenie, ktoré je zložením osovej súmernosti a posunutia (v ľubovoľnom poradí), pričom os osovej súmernosti a vektor posunutia sú rovnobežné, nazývame posunutá súmernosť ; (posunutú súmernosť danú osou a vektorom
a vektorom 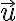 budeme označovať
budeme označovať 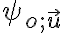 ).
).
Zobrazenie, ktoré je zložením osovej súmernosti a posunutia (v ľubovoľnom poradí), pričom os osovej súmernosti a vektor posunutia sú rovnobežné, nazývame posunutá súmernosť ; (posunutú súmernosť danú osou
 a vektorom
a vektorom 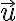 budeme označovať
budeme označovať 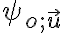 ).
).
Poznámka.
V niektorej literatúre sa pre posunutú súmernosť používa názov posunuté zrkadlenie.
V niektorej literatúre sa pre posunutú súmernosť používa názov posunuté zrkadlenie.
Tvrdenie
Zložením troch osových súmerností s navzájom rôznymi osami je buď osová súmernosť’ alebo posunutá súmernosť.
Zložením troch osových súmerností s navzájom rôznymi osami je buď osová súmernosť’ alebo posunutá súmernosť.
Dôkaz
Nech sú dané osové súmernosti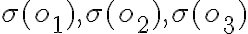 a nech
a nech 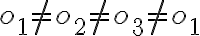 sú navzájom rôzne priamky.
Pre vzájomnú polohu týchto troch priamok môžu nastať 3 prípady:
sú navzájom rôzne priamky.
Pre vzájomnú polohu týchto troch priamok môžu nastať 3 prípady:
Nech sú dané osové súmernosti
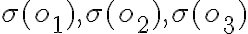 a nech
a nech 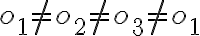 sú navzájom rôzne priamky.
Pre vzájomnú polohu týchto troch priamok môžu nastať 3 prípady:
sú navzájom rôzne priamky.
Pre vzájomnú polohu týchto troch priamok môžu nastať 3 prípady:
- Všetky priamky sú navzájom rovnobežné → výsledné zložené zobrazenie je osová súmernosť.
- Dve sú rovnobežné a tretia ich pretína → výsledné zložené zobrazenie je posunutá súmernosť.
- Priamky ležia na stranách trojuholníka (navzájom sú rôznobežné) → výsledné zložené zobrazenie je posunutá súmernosť. Otvorte si applet Tu.
Grupa zhodných zobrazenií
Tvrdenie.
- Zloženie ľubovoľného konečného počtu osových súmerností možno vždy redukovať na zloženie maximálne troch osových súmerností.
Pozrite si konštrukčný dôkazu Tu.
- Zložením ľubovoľného konečného počtu zhodných zobrazení je identita, alebo osová súmernosť, alebo stredová súmernosť, alebo rotácia, alebo translácia, alebo posunutá súmernosť.
- Všetky zhodnosti v rovine tvoria vzhľadom na skladanie zobrazení grupu (tzv. grupu zhodností). Generátorom grupy zhodností je osová súmernosť.
Zhodnosti reprodukujúce štvorec tvoria podgrupu. Pozrite si dynamický model.
Rovnoľahlosť
Definícia.
Podobné zobrazenie (podobnosť) je zobrazenie, v ktorom obrazom každej úsečky je úsečka
je úsečka 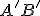 , ktorej veľkosť je
, ktorej veľkosť je  -násobkom veľkosti úsečky
-násobkom veľkosti úsečky 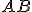 (
( 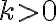 ).
).
Podobné zobrazenie (podobnosť) je zobrazenie, v ktorom obrazom každej úsečky
 je úsečka
je úsečka 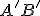 , ktorej veľkosť je
, ktorej veľkosť je  -násobkom veľkosti úsečky
-násobkom veľkosti úsečky 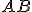 (
( 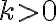 ).
).
V každom podobnom zobrazení platí:
Definícia (Rovnoľahlosť).
Je daný bod a reálne číslo
a reálne číslo 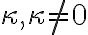 . Rovnoľahlosť (homotétia) je zobrazenie
. Rovnoľahlosť (homotétia) je zobrazenie 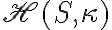 , ktoré priraďuje:
, ktoré priraďuje:
Je daný bod
 a reálne číslo
a reálne číslo 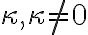 . Rovnoľahlosť (homotétia) je zobrazenie
. Rovnoľahlosť (homotétia) je zobrazenie 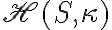 , ktoré priraďuje:
, ktoré priraďuje:
Poznámka.
Rovnoľahlosť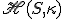 je podobnosť s koeficientom
je podobnosť s koeficientom 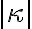 . Pre
. Pre 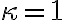 je identitou, pre
je identitou, pre 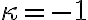 rotáciou okolo
rotáciou okolo
 o 180° (aj stredovou súmernosťou so stredom v bode
o 180° (aj stredovou súmernosťou so stredom v bode  ).
).
Pre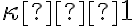 je jediným samodružným bodom stred
je jediným samodružným bodom stred  . Samodružnou priamkou je každá priamka, ktorá prechádza stredom rovnoľahlosti. Pozrite si súbor appletov od
Martina Vinklera Tu.
. Samodružnou priamkou je každá priamka, ktorá prechádza stredom rovnoľahlosti. Pozrite si súbor appletov od
Martina Vinklera Tu.
Rovnoľahlosť
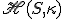 je podobnosť s koeficientom
je podobnosť s koeficientom 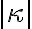 . Pre
. Pre 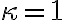 je identitou, pre
je identitou, pre 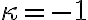 rotáciou okolo
rotáciou okolo
 o 180° (aj stredovou súmernosťou so stredom v bode
o 180° (aj stredovou súmernosťou so stredom v bode  ).
).
Pre
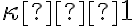 je jediným samodružným bodom stred
je jediným samodružným bodom stred  . Samodružnou priamkou je každá priamka, ktorá prechádza stredom rovnoľahlosti. Pozrite si súbor appletov od
Martina Vinklera Tu.
. Samodružnou priamkou je každá priamka, ktorá prechádza stredom rovnoľahlosti. Pozrite si súbor appletov od
Martina Vinklera Tu.
Rovnoľahlosť je špeciálne podobné zobrazenie. To znamená, že má všetky vlastnosti podobného zobrazenia.
Naviac má vlastnosť, že v rovnoľahlosti odpovedajúce priamky (vzor a obraz) sú rovnobežné.
Naviac má vlastnosť, že v rovnoľahlosti odpovedajúce priamky (vzor a obraz) sú rovnobežné.

Vľavo. V rovnoľahlosti platí:
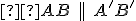 . Vpravo. Podobné zobrazenie zložené z rovnoľahlosti a otáčania.
. Vpravo. Podobné zobrazenie zložené z rovnoľahlosti a otáčania.
Otvorte si applet Tu.
Veta 1.
V rovnoľahlosti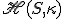 :
: 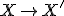
V rovnoľahlosti
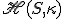 :
: 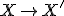
- každé dve rovnoľahlé priamky sú rovnobežné,
- každé dve rovnobežné a nezhodné úsečky sú rovnoľahlé dvomi spôsobmi,
- každé dve nezhodné kružnice
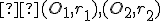 sú rovnoľahlé, pričom stredy rovnoľahlosti ležia na strednej kružníc,
sú rovnoľahlé, pričom stredy rovnoľahlosti ležia na strednej kružníc, - spoločné dotyčnice dvoch kružníc prechádzajú odpovedajúcimi stredmi rovnoľahlostí (vnútorným
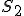 a vonkajším
a vonkajším 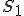 stredom rovnoľahlosti).
stredom rovnoľahlosti).
Veta 2.
Nech sú dve kružnice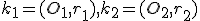 rovnoľahlé, ich vonkajší stred rovnoľahlosti je bod
rovnoľahlé, ich vonkajší stred rovnoľahlosti je bod 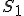 , vnútorný stred rovnoľahlosti
, vnútorný stred rovnoľahlosti 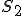 . Potom platí
. Potom platí
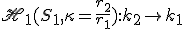 ,
,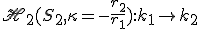 .
.
Nech sú dve kružnice
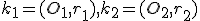 rovnoľahlé, ich vonkajší stred rovnoľahlosti je bod
rovnoľahlé, ich vonkajší stred rovnoľahlosti je bod 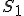 , vnútorný stred rovnoľahlosti
, vnútorný stred rovnoľahlosti 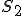 . Potom platí
. Potom platí
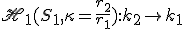 ,
,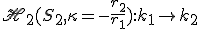 .
.
Veta 3.
Zložením rovnoľahlosti a zhodného zobrazenia dostaneme podobné zobrazenie.
Každé podobné zobrazenie možno získať zložením vhodného zhodného zobrazenia a rovnoľahlosti >.
Zložením rovnoľahlosti a zhodného zobrazenia dostaneme podobné zobrazenie.
Každé podobné zobrazenie možno získať zložením vhodného zhodného zobrazenia a rovnoľahlosti >.
Cvičenie 1.
Do daného trojuholníka vpíšte štvorec
vpíšte štvorec 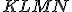 tak , aby strana
tak , aby strana 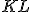 ležala na strane
ležala na strane 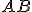 ,
bod
,
bod 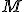 ležal na strane
ležal na strane 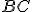 a bod
a bod 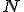 na strane
na strane 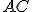 .
.
Riešenie v práci [RUM], str. 98.
Do daného trojuholníka
 vpíšte štvorec
vpíšte štvorec 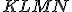 tak , aby strana
tak , aby strana 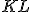 ležala na strane
ležala na strane 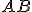 ,
bod
,
bod 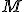 ležal na strane
ležal na strane 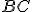 a bod
a bod 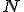 na strane
na strane 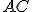 .
.
Riešenie v práci [RUM], str. 98.
Afinita
Geometrické zobrazenia  v euklidovskej rovine
v euklidovskej rovine  môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
 v euklidovskej rovine
v euklidovskej rovine  môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
môžeme skúmať aj podľa počtu a druhu samodružných prvkov.
Definícia (Samodružné prvky).
- Samodružný bod
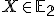 je bod, ktorý sa pri zobrazení
je bod, ktorý sa pri zobrazení  zobrazí sám na seba. Platí:
zobrazí sám na seba. Platí: 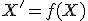 .
. - Samodružná priamka
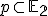 je priamka, ktorá sa pri zobrazení
je priamka, ktorá sa pri zobrazení  zobrazí sama na seba
zobrazí sama na seba 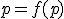 . Zároveň existuje bod
. Zároveň existuje bod 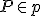 , ktorý sa zobrazí do bodu
, ktorý sa zobrazí do bodu 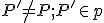 .
. - Priamka samodružných bodov je priamka, kde každý jej bod je samodružný. Pre každý bod na priamke platí X = X'. Hovoríme o bodovo samodružnej priamke.
Zvoľme si v euklidovskej rovine  dve rôznobežné priamky
dve rôznobežné priamky 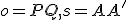 . Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie
. Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie 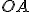 s vlastnosťami
s vlastnosťami

Obr. Afinita
 dve rôznobežné priamky
dve rôznobežné priamky 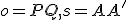 . Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie
. Pozrite si obrázok Afinita. Budeme skúmať geometrické zobrazenie 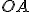 s vlastnosťami
s vlastnosťami
- Obrazom ľubovoľného bodu
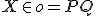 je ten istý bod
je ten istý bod  , priamka
, priamka 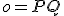 je bodovo samodružná..
je bodovo samodružná.. - Obrazom ľubovoľného bodu
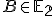 je bod
je bod 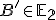 , ktorý leží na priamke
, ktorý leží na priamke 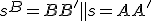 .
. - Obrazom priamky
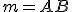 je priamka
je priamka 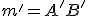 , pričom bod
, pričom bod 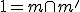 je samodružný. V prípade
rovnobežnosti
je samodružný. V prípade
rovnobežnosti 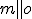 je tiež
je tiež 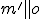 (bod 1 je nevlastný).
(bod 1 je nevlastný). - Obrazom priamky rovnobežnej s priamkou
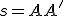 je tá istá priamka, priamka je samodružná.
je tá istá priamka, priamka je samodružná. - Takéto zobrazenie je zrejme bijektívne zobrazenie euklidovskej roviny. Budeme ho nazývať osová afinita v rovine.
Obr. Afinita
Vlastnosti.
- osová afinita je jednoznačne určená priakou
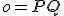 a dvojicou odpovedajúcich si bodov
a dvojicou odpovedajúcich si bodov 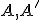 ,
, - priamku
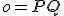 nazývame os afinity a priamku
nazývame os afinity a priamku 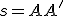 nazývame smer afinity,
nazývame smer afinity, - osová afinita zachováva incidenciu, rovnobežnosť a deliaci pomer troch kolineárnych bodov. Dôkaz je založený na vlastnosti podobných trojuholníkov. Pozrite si prácu [PLICH].
Osovú afinitu môžeme využiť aj pri dôkazoch niektorých vlastností všeobecných trojuholníkov. Stačí ak dokážeme určiť osovú afinitu, v ktorej sa daný všeobecný trojuholník zobrazí na rovnostraný trojuholník. Keďže osová afinita zachováva incidenciu a deliaci pomer (špeciálne stred úsečky sa zobrazí do stredu úsečky), tak napríklad vlastnosť ťažníc stačí dokázať len pre rovnostranný trojuholník.
Uvedieme konštrukciu ako takúto osová afinitu určuíť.
Uvedieme konštrukciu ako takúto osová afinitu určuíť.
Cvičenie.
Určte OA tak, aby sa všeobecný trojuholník zobrazil do rovnostranného trojuholníka
zobrazil do rovnostranného trojuholníka 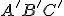 . Riešenie nájdete Tu.
. Riešenie nájdete Tu.
Určte OA tak, aby sa všeobecný trojuholník
 zobrazil do rovnostranného trojuholníka
zobrazil do rovnostranného trojuholníka 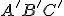 . Riešenie nájdete Tu.
. Riešenie nájdete Tu.
Riešené príklady.
Osová afinita je daná osou a dvojicou odpovedajúcich bodov
a dvojicou odpovedajúcich bodov 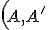
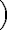 .
Zostrojte bod
.
Zostrojte bod 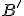 , ktorý je obrazom daného bodu
, ktorý je obrazom daného bodu 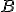 . Nech
. Nech 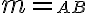 je priamka určená bodmi
je priamka určená bodmi 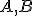 . Uvažujme dva prípady:
. Uvažujme dva prípady:
Osová afinita je daná osou
 a dvojicou odpovedajúcich bodov
a dvojicou odpovedajúcich bodov 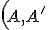
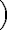 .
Zostrojte bod
.
Zostrojte bod 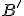 , ktorý je obrazom daného bodu
, ktorý je obrazom daného bodu 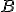 . Nech
. Nech 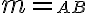 je priamka určená bodmi
je priamka určená bodmi 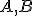 . Uvažujme dva prípady:
. Uvažujme dva prípady:
- Priamka
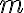 je rôznobežná s osou
je rôznobežná s osou 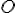 , riešenie Tu.
, riešenie Tu. - Ak priamka
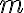 je rovnobežná s osou
je rovnobežná s osou 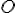 tak použijeme konštrukciu:
tak použijeme konštrukciu:
- zvoľme si vhodnú priamku
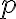 prechádzajúcu bodom
prechádzajúcu bodom 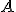 , ktorá nie je rovnobežná s osou
, ktorá nie je rovnobežná s osou 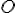
- na priamke
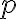 si zvoľme bod
si zvoľme bod 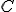 tak, aby priamka
tak, aby priamka 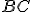 nebola rovnobežná s osou
nebola rovnobežná s osou 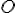
- obrazom priamky
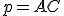 je priamka
je priamka 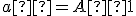 , obraz
, obraz 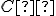 bodu
bodu  musí ležať na priamke
musí ležať na priamke 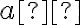
- bodmi
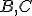 je určená priamka
je určená priamka 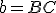 , obrazom priamky
, obrazom priamky 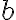 je priamka
je priamka 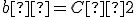
- obraz
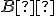 bodu
bodu 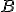 musí ležať na priamke
musí ležať na priamke 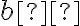 , riešenie
Tu.
, riešenie
Tu.
- zvoľme si vhodnú priamku
Veta.
Obraz kružnice v osovej afinite je elipsa (dôkaz je jednoduchý ak využijeme metódy analytickej geometrie).
Obraz kružnice v osovej afinite je elipsa (dôkaz je jednoduchý ak využijeme metódy analytickej geometrie).
Na zostrojenie takejto elipsu môžeme využiť dva spôsoby.
- Priama konštrukcia hlavnej a vedľajšej poloosi.
Nájdením združených priemerov elipsy. Využijeme skutočnosť, že v kružnici združené priemery sú také priemery, ktoré sú vzájomne kolmé. (Priemery elipsy resp. kružnice sa nazývajú združené, ak sú dotyčnice v krajných bodoch jedného priemeru rovnobežné s druhým priemerom a naopak.) - Nepriamo pomocou Rytzovej konštrukcie.
V kružnici zvolíme dva ľubovoľné na seba kolmé priemery KL, MN a nájdeme ich obrazy K'L', M'N'. Osová afinita zachováva rovnobežnosť a deliaci pomer. Preto tvoria úsečky K'L', M'N' združené priemery elipsy. Ak poznáme dva združené priemery elipsy, využijeme na nájdenie hlavnej a vedľajšej osi Rytzovu konštrukciu. Pozrite si prácu [PLI].
Poznámka.
Vzťah osovej afinity v euklidovskej rovine si môžeme predstaviť aj ako kolmý priemet priestorovej afinity. Uvedieme definíciu osovej afinity medzi dvoma rôznobežnými rovinami v euklidovskom priestore z práce [DRA]. Pozrite si dynamický obrázok "Priestorová afinita".
Vzťah osovej afinity v euklidovskej rovine si môžeme predstaviť aj ako kolmý priemet priestorovej afinity. Uvedieme definíciu osovej afinity medzi dvoma rôznobežnými rovinami v euklidovskom priestore z práce [DRA]. Pozrite si dynamický obrázok "Priestorová afinita".
Definícia.
Uvažujme dve rôznobežné roviny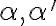 a ich priesečnicu označme
a ich priesečnicu označme  . Zvoľme ďalej smer
. Zvoľme ďalej smer 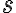 , ktorý je rôznobežný s oboma rovinami
, ktorý je rôznobežný s oboma rovinami
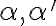 . Potom priradíme navzájom body a priamky roviny
. Potom priradíme navzájom body a priamky roviny  bodom a priamkam roviny
bodom a priamkam roviny 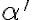 tak, že platí:
tak, že platí:
Uvažujme dve rôznobežné roviny
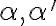 a ich priesečnicu označme
a ich priesečnicu označme  . Zvoľme ďalej smer
. Zvoľme ďalej smer 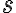 , ktorý je rôznobežný s oboma rovinami
, ktorý je rôznobežný s oboma rovinami
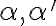 . Potom priradíme navzájom body a priamky roviny
. Potom priradíme navzájom body a priamky roviny  bodom a priamkam roviny
bodom a priamkam roviny 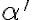 tak, že platí:
tak, že platí:
- Osovú afinitu medzi dvoma rôznobežnými rovinami s výhodou využívame pri rezoch rovnobežnostena.
- Porovnajme vlastnosti osovej afinity s rezom hranola, obrázok "Rez hranola (obrázok je prevzatý s práce [PLI]).
- Rovina
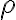 zodpovedá rovine rezu, rovina
zodpovedá rovine rezu, rovina 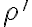 zodpovedá rovine dolnej podstavy. Smer afinity s zodpovedá smeru hrán, napríklad
zodpovedá rovine dolnej podstavy. Smer afinity s zodpovedá smeru hrán, napríklad 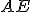 . Zodpovedajúce si body sú napríklad body
. Zodpovedajúce si body sú napríklad body 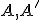 . Os
. Os  je priesečnica rovín
je priesečnica rovín 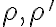 a zodpovedá priesečnici roviny podstavy a roviny rezu.
a zodpovedá priesečnici roviny podstavy a roviny rezu.
Obr. Rez hranola
Stredová kolineácia
Definícia (Stredová kolineácia medzi dvoma rovinami).
Nech sú dané dve rôzne roviny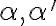 a bod
a bod  , ktorý neleží ani v jednej z nich.
, ktorý neleží ani v jednej z nich.
Nech sú dané dve rôzne roviny
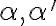 a bod
a bod  , ktorý neleží ani v jednej z nich.
, ktorý neleží ani v jednej z nich.
- Stredová kolineácia je bijektívne zobrazenie dvoch rovín, pri ktorom každému bodu prvej roviny odpovedá jeho priemet zo stredu
 do roviny druhej. Používa sa aj termín perspektívna kolineácia.
do roviny druhej. Používa sa aj termín perspektívna kolineácia. - Stred premietania
 sa nazýva stred kolineácie. Priamku
sa nazýva stred kolineácie. Priamku  , priesečnicu rovín
, priesečnicu rovín 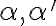 , nazývame osou stredovej kolineácie.
, nazývame osou stredovej kolineácie.
Obr. Stredová kolineácia medzi dvoma rovinami
Vlastnosti.
- Vlastnému bodu môže odpovedať nevlastný bod a naopak. Ak bod
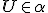 leží v rovine rovnobežnej s rovinou
leží v rovine rovnobežnej s rovinou 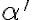 , tak
priamka
, tak
priamka  sa s rovinou
sa s rovinou 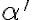 pretína v nevlastnom bode. Analogicky pre bod
pretína v nevlastnom bode. Analogicky pre bod 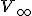 .
. - Priamky, ktoré si odpovedajú v perspektívnej kolineácii, sa pretínajú na osi kolineácie alebo sú s ňou rovnobežné (majú spoločný nevlastný bod).
- Body osi kolineácie sú samodružné body. Perspektívna kolineácia zachováva incidenciu.
- Perspektívna kolineácia nezachováva deliaci pomer ale zachováva dvojpomer. Stred úsečky sa vo všeobecnosti nezobrazuje do stredu úsečky.
Pre situáciu, keď obrazom vlastného bodu ja nevlastný bod a naopak, používame terminológiu:
- Vlastný bod
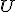 , ktorý sa v kolineácii zobrazí do nevlastného
, ktorý sa v kolineácii zobrazí do nevlastného 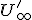 nazývame úbežník
(niekedy úbežník 1. druhu).
nazývame úbežník
(niekedy úbežník 1. druhu). - Vlastný bod
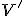 , ktorý je v kolineácii obrazom nevlastného bodu
, ktorý je v kolineácii obrazom nevlastného bodu 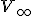 nazývame úbežník
(niekedy úbežník 2. druhu).
nazývame úbežník
(niekedy úbežník 2. druhu). - Priamky, ktoré sú obrazom alebo vzorom nevlastnej priamky sa nazývajú úbežnice . Úbežnice(priamky) obsahujú všetky úbežníky daného druhu a sú rovnobežné s osou afinity.
Špeciálny typ perspektívnej kolineácie ak stred
 je nevlastný bod,
tak perspektívna kolineácia je osová afinita.
je nevlastný bod,
tak perspektívna kolineácia je osová afinita.
Perspektívnu kolineáciu si môžeme zjednodušene predstaviť ako vzťah medzi rezom ihlana (resp. kužeľa) rovinou a podstavou.
Poznámka.
Stredovú kolineáciu medzi dvoma rovinami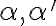 v euklidovskom priestore môžeme previesť na stredovú kolineáciu v rovine.
v euklidovskom priestore môžeme previesť na stredovú kolineáciu v rovine.
Stredovú kolineáciu medzi dvoma rovinami
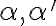 v euklidovskom priestore môžeme previesť na stredovú kolineáciu v rovine.
v euklidovskom priestore môžeme previesť na stredovú kolineáciu v rovine.
- Zvolíme si rovinu
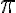 , do ktorej budeme premietať a smer premietania určený vektorom "Priemet", pričom smer premietania volíme tak, aby nebol rovnobežný so
žiadnou z rovín
, do ktorej budeme premietať a smer premietania určený vektorom "Priemet", pričom smer premietania volíme tak, aby nebol rovnobežný so
žiadnou z rovín 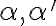 .
. - Os kolineácie
 , stred kolineácie
, stred kolineácie  a zodpovedajúce si body
a zodpovedajúce si body 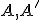 premietneme pomocou smeru "Priemet" do roviny
premietneme pomocou smeru "Priemet" do roviny  .
. - Keďže rovnobežné premietanie (smer "Priemet") zachováva rovnobežnosť, tak pre body
 platí opäť vzťah stredovej kolineácie.
platí opäť vzťah stredovej kolineácie. - Stred kolineácie
 je rovnobežným priemetom stredu
je rovnobežným priemetom stredu  , podobne body
, podobne body  sú priemety bodov
sú priemety bodov 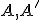 .
. - Dvojicu odpovedajúcich si bodov
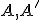 nazývame kolineárne združené body.
nazývame kolineárne združené body. - Vo všeobecnosti kolineácia je jednoznačne určená stredom
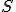 , osou
, osou  a dvojicou odpovedajúcich si bodov
a dvojicou odpovedajúcich si bodov 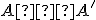 .
V takom prípade budeme pre kolineáciu používať označenie
.
V takom prípade budeme pre kolineáciu používať označenie 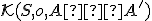 .
.
Cvičenie.
Veta.
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka (elipsa, parabola alebo hyperbola).
Obrazom kružnice v stredovej kolineácii je regulárna kužeľosečka (elipsa, parabola alebo hyperbola).
Regulárne kužeľosečky môžeme klasifikovať podľa počtu nevlastných bodov. Elipsa má všetky body vlastné. Parabola má jeden nevlastný bod a hyperbola má dva nevlastné body.
Z predchádzajúceho textu vieme, že obrazom úbežníku I. druhu je nevlastný bod. Z toho vyplýva, že ak kružnica s úbežnicou
Z predchádzajúceho textu vieme, že obrazom úbežníku I. druhu je nevlastný bod. Z toho vyplýva, že ak kružnica s úbežnicou
- nemá žiadny spoločný bod, potom je obrazom kružnice elipsa,
- má práve jeden spoločný bod, potom je obrazom kružnice parabola,
- má dva rôzne priesečníky, potom je obrazom kružnice hyperbola.
Kruhová inverzia
Möbiova rovina je euklidovská rovina doplnená o jeden nevlastný bod
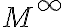 , ktorý budeme nazývať Möbiov bod.
, ktorý budeme nazývať Möbiov bod.
V takto doplnenej rovine môžeme definovať zobrazenie, ktoré sa nazýva kruhová inverzia.
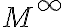 , ktorý budeme nazývať Möbiov bod.
, ktorý budeme nazývať Möbiov bod.
V takto doplnenej rovine môžeme definovať zobrazenie, ktoré sa nazýva kruhová inverzia.
Definícia.
V Möbiovej rovine je daná kružnica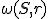 . Kruhová inverzia vzhľadom ku kružnici
. Kruhová inverzia vzhľadom ku kružnici 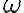 je zobrazenie, ktorého obrazom
je zobrazenie, ktorého obrazom
V Möbiovej rovine je daná kružnica
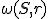 . Kruhová inverzia vzhľadom ku kružnici
. Kruhová inverzia vzhľadom ku kružnici 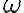 je zobrazenie, ktorého obrazom
je zobrazenie, ktorého obrazom
Poznamenajme, že
 , ležiaci mimo kružnice
, ležiaci mimo kružnice 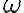 :
:
Z bodu zostrojíme dotyčnicu kružnice
zostrojíme dotyčnicu kružnice 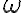 , bod dotyku označme
, bod dotyku označme 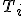 . Z bodu
. Z bodu 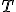 zostrojíme kolmicu na priamku
zostrojíme kolmicu na priamku 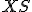 , päta tejto kolmice je hľadaný obraz
, päta tejto kolmice je hľadaný obraz 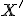 .
Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice
.
Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice 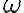 .
.
Kruhová inverzia je nelineárne zobrazenie, priamka až na špeciálne prípady sa nezobrazuje na priamku (priamky, ktoré neprechádzajú stredom inverzie, sa zobrazujú na kružnice).
- ak bod
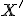 je obrazom bodu
je obrazom bodu  , potom je aj bod
, potom je aj bod  obrazom bodu
obrazom bodu 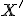 ,
dvojicu odpovedajúcich bodov nazývame aj navzájom inverzné body - kruhová inverzia je involútorné zobrazenie;
,
dvojicu odpovedajúcich bodov nazývame aj navzájom inverzné body - kruhová inverzia je involútorné zobrazenie; - body na kružnici
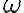 sú samodružné;
sú samodružné; - bod ležiaci vo vnútri kružnice
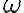 sa zobrazí na vonkajší bod a naopak.
Konštrukcia obrazu
sa zobrazí na vonkajší bod a naopak.
Konštrukcia obrazu
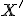 ľubovoľného bodu
ľubovoľného bodu  a
a 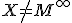 a
a 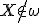 je založená na Euklidovej vete o odvesne.
je založená na Euklidovej vete o odvesne.
 , ležiaci mimo kružnice
, ležiaci mimo kružnice 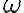 :
:
Z bodu
 zostrojíme dotyčnicu kružnice
zostrojíme dotyčnicu kružnice 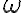 , bod dotyku označme
, bod dotyku označme 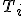 . Z bodu
. Z bodu 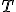 zostrojíme kolmicu na priamku
zostrojíme kolmicu na priamku 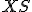 , päta tejto kolmice je hľadaný obraz
, päta tejto kolmice je hľadaný obraz 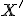 .
Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice
.
Konštrukciu je možné použiť aj pre bod ležiaceho vo vnútri kružnice 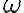 .
.
Kruhová inverzia je nelineárne zobrazenie, priamka až na špeciálne prípady sa nezobrazuje na priamku (priamky, ktoré neprechádzajú stredom inverzie, sa zobrazujú na kružnice).
Veta (Konformné zobrazenie).
Kruhová inverzia je konformné zobrazenie, t.j zachováva veľkosť uhla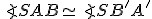 . Pozrite si obrázok "Konformné zobrazenie".
. Pozrite si obrázok "Konformné zobrazenie".
Kruhová inverzia je konformné zobrazenie, t.j zachováva veľkosť uhla
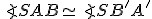 . Pozrite si obrázok "Konformné zobrazenie".
. Pozrite si obrázok "Konformné zobrazenie".
Dôkaz.
Z definície kruhovej inverzie vyplýva
Obr. Konformné zobrazenie
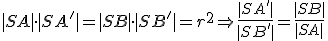
Teda trojuholníky
 majú spoločný uhol pri vrchole, sú podľa vety
majú spoločný uhol pri vrchole, sú podľa vety 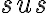 podobné.
podobné.
Tvrdenie (Obraz priamky a kružnice).
Body priamky prechádzajúcej stredom inverzie sa zobrazujú opäť na túto priamku.
sa zobrazujú opäť na túto priamku.
Body priamky prechádzajúcej stredom inverzie
 sa zobrazujú opäť na túto priamku.
sa zobrazujú opäť na túto priamku.
Dôkaz
Ide vlastne o špeciálny prípad vety o konformnom zobrazení, keď bod leží na kolmici k polpriamke
leží na kolmici k polpriamke 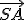 . Zrejme platí
. Zrejme platí
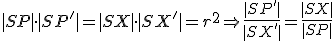 ,
,
lebo trojuholníky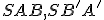 sú podobné. Uhol pri vrchole
sú podobné. Uhol pri vrchole 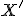 je pravý, preto bod
je pravý, preto bod 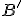 je zrejme bodom Thálesovej kružnice.
je zrejme bodom Thálesovej kružnice.
Ide vlastne o špeciálny prípad vety o konformnom zobrazení, keď bod
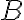 leží na kolmici k polpriamke
leží na kolmici k polpriamke 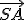 . Zrejme platí
. Zrejme platí
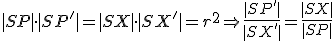 ,
,
lebo trojuholníky
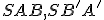 sú podobné. Uhol pri vrchole
sú podobné. Uhol pri vrchole 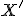 je pravý, preto bod
je pravý, preto bod 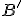 je zrejme bodom Thálesovej kružnice.
je zrejme bodom Thálesovej kružnice.
Dôsledky.
- Obrazom priamky
 , ktorá neprechádza stredom inverzie je kružnica
, ktorá neprechádza stredom inverzie je kružnica  prechádzajúca stredom
prechádzajúca stredom  .
. - Obrazom kružnice prechádzajúcej stredom inverzie je priamka, ktorá neprechádza stredom inverzie.
- Samodružnými bodmi sú body určujúcej kružnice
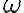 .
. - Samodružnými priamkami sú priamky prechádzajúce stredom inverzie.
- Samodružné kružnice sú tie, ktoré ortogonálne pretínajú určujúcu kružnicu. Dôkaz si môžete pozrieť v práci [JAN].
Dôkazy týchto dôsledkov sa opierajú o involútornosť kruhovej inverzie.
Tvrdenie (Obraz kružnice neprechádzajúcej stredom  ).
).
Obrazom kružnice, ktorá neprechádza stredom inverzie je kružnica.
je kružnica.
 ).
).
Obrazom kružnice, ktorá neprechádza stredom inverzie
 je kružnica.
je kružnica.
Poznámka.
Z obrázku "Obraz kružnice" je zrejmá jedna typická ale často opomínaná vlastnosť kruhovej inverzie:
Obrazom stredu kružnice nie je stred kružnice
nie je stred kružnice 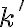 .
.
Z obrázku "Obraz kružnice" je zrejmá jedna typická ale často opomínaná vlastnosť kruhovej inverzie:
Obrazom stredu kružnice
 nie je stred kružnice
nie je stred kružnice 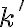 .
.
Apolloniova úloha.
Zostrojte kružnicu dotýkajúcu sa troch geometrických útvarov: bodu -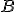 , priamky -
, priamky -  , kružnice -
, kružnice -  .
.
Zostrojte kružnicu dotýkajúcu sa troch geometrických útvarov: bodu -
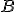 , priamky -
, priamky -  , kružnice -
, kružnice -  .
.
- Existuje celkove desať možných kombinácií. Napr.
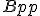 znamená zostrojiť kružnicu, ktorá prechádza bodom a dotýka sa dvoch priamok.
Dotyk s bodom znamená incidenciu s ním.
znamená zostrojiť kružnicu, ktorá prechádza bodom a dotýka sa dvoch priamok.
Dotyk s bodom znamená incidenciu s ním. - Najjednoduchšie prípady nastanú, keď sú dané tri body alebo tri priamky; tieto prípady vyriešil Euklides vo svojich Základoch. Apolloniove úlohy patria dodnes k najpríťažlivejším úlohám syntetickej geometrie.
Historické poznámky.
- O dotyku kružníc údajne písal už Archimedes. Jeho spis sa však nezachoval. Taktiež sa nezachoval dvojzväzkový pôvodný spis Apollonia z Pergy (262?-190? pred n. l.) „O dotykoch".
- Zmienil sa o ňom Pappos okolo roku 320, podľa ktorého Apollonios vyriešil všetky úlohy s výnimkou prípadu troch kružníc.
- Úlohu s tromi kružnicami riešil ako prvý F. Viete (1540-1603) v spise „Apollonius Gallus" (Paríž, r. 1600). V riešení použil stredy rovnoľahlosti troch kružníc.
- Vo všeobecnom prípade je osem výsledkov. Ak sa dané tri kružnice navzájom dotýkajú, riešenia sú dve (tzv. Soddyho kružnice).
Metódy riešenia Apolloniovej úlohy
Literatúra
- [BEC] Bečvár J., Bečvářová M., Vymazalová H.(ed.), Matematika ve starověku Egypt a Mezopotámie. Prometheus, Praha 2003. Dostupné Tu.
- [CAS] Castellanos,J., NonEuclid: Interactive Javascript Software for Creating Straightedge and Collapsible Compass Constructions in the Disk Model of Hyperbolic Geometry. Dostupné Tu.
- [CIZ] Čižmár, J., Euklides Základy. Perfekt 2022. ISBN 9788082260314.
- [DAV]Davidová, E., Řešení planimetrických konstrukčních úloh. Ostrava 2005. Dostupné Tu.
- [DRA] Drábek K., Harant F., Setzer O.: Deskriptivní geometrie I, SNTL, Praha 1978.
- [EUC] Euklidove Základy., Elektronická - verzia (angl.). Dostupné Tu.
- [GRE] Greenberg, M., Euclidean and non-Euclidean geometries. Third. Development and history. W. H. Freeman and Company, New York, 1993. Dostupné Tu. Stiahnuté PDF Tu.
- [HIL] Hilbert, D., Grundlagen der Geometrie (Základy geometrie). 1899. Dostupné Tu.
- [HIT] Hitchman, M. P., Geometry with an Introduction to Cosmic Topology. Oregon, USA 2018. Dostupné Tu.
- [HYP] Hyperbolic Geometry, Part III. Dostupné Tu. Stiahnuté PDF Tu.
- [CHAL] Chalmovianská, J., Geometria 2 (pre študentov učiteľstva matematiky). Dostupné Tu.
- [CHRI] M. Christersson, M., GeoGebra Constructions in the Disc. Dostupné Tu.
- [JAN]Janyška, J.: Geometrické zobrazení. Skriptá Brno 2022. Dostupné Tu.
- [JOY] Joyce, D.E., Euclid's Elements, 1994. Dostupné Tu.
- [KRI] Križalkovič, K., Cuninka, A., Šedivý, O.: 500 riešených úloh z geometrie. 2. vyd. Bratislava: Alfa, 1972. Polytechnická knižnica.
- [LAR] Larson, Loren C., Problem-Solving Through Problems. Springer-Verlag New York Inc. 1983. ISBN: 978-0-387-96171-2. Dostupné Tu.
- [LUK] Lukáč, S., Bádateľský prístup k výučbe trojuholníkov. Matematika – fyzika – informatika 23 2014.
- [MAN] Manthey, J., GeoGebra Tools for Poincare Disk. Dostupné Tu.
- [MON] Monoszová, G., Planimetria. Dostupné Tu.
- [PLI] Plichtová, Petra., Webová aplikace pro výuku osové afinity a středové kolineace. Univerzita Karlova v Praze, Matematicko-fyzikální fakulta, DP, 2023. Dostupné Tu.
- [RUM] Rumanová,L., Vallo,D: Geometria – vybrané kapitoly. FPV UKF v Nitre, 2009. ISBN: 978-80-8094-567-1.
- [SKL] Sklenáriková, Z.: K metódam riešenia Apolloniovej úlohy. Matematika v proměnách věků. III. Praha, 2004.
- [SED] Šedivý, O., Vallo, D., Základy elementárnej geometrie. FPV UKF v Nitre, 2009. ISBN : 978-80-8094-623-4.Dostupné Tu.
- [SER] Servít, F., Eukleidovy Základy (Elementa). JČM, Praha, 1907. Dostupné Tu.
- Ukážka funkčného modelu "The hyperbolic plane" Tu, ktorý je prevzatý zo stránky TH .
- [VAL, 2005] Vallo, D.,Geometria perspektívnych trojuholníkov. FPV UKF v Nitre,2005, str.9. ISBN : 80-8050-825-9. Dostupné Tu.
- [VAL, 2016] Vallo, D., Metodika konštrukčných úloh z geometrie v prostredí DGS. UKF Nitra 2016. Dostupné Tu.
- [VAL, 2021] Vallo, D., Koncepcia výučby geometrie podporovanej implementáciou dynamických geometrických programov. Univerzita Konštantína Filozofa v Nitre. FPV Nitra, 2021. Stiahnuté PDF Tu.
- [VIN] Vinkler, M., Materiály v prostredí GeoGebra. Dodtupné Tu.
- ŽILKOVÁ, K. Dilemy v tvorbe e-kurzu Manipulačná geometria. In: Matematika v primárnej škole - rôzne cesty, rovnaké ciele. Prešov: Prešovská univerzita v Prešove, 2013. ISBN 978-80-555-0765-1, s. 276-280.