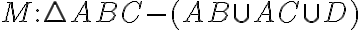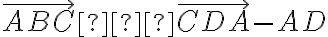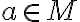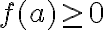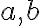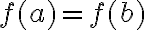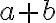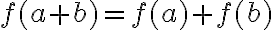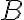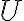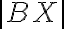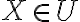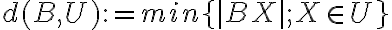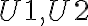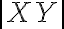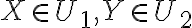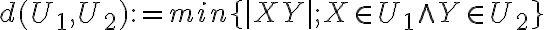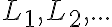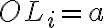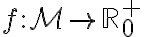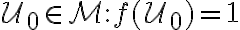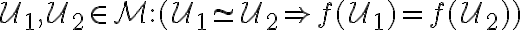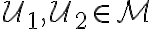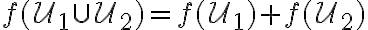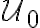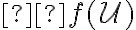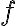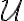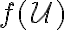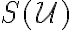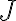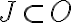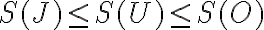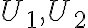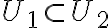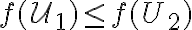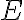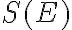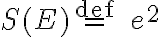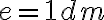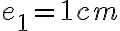Jordanova miera
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria N |
| Kniha: | Jordanova miera |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 10:35 |
Topologické pojmy
Základné topologické pojmy - definície (Spracované podľa práce [1])
Nech
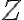 je základná množina, bod
je základná množina, bod
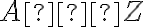 ,
, 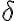 je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina
je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina 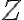 je pravidelný 7-uholník.
je pravidelný 7-uholník.
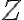 je základná množina, bod
je základná množina, bod
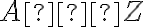 ,
, 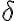 je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina
je ľubovoľne zvolená nenulová úsečka.
V priloženom applete množina 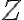 je pravidelný 7-uholník.
je pravidelný 7-uholník.
-
Okolie bodu
 (presnejšie
(presnejšie 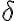 -okolie bodu
-okolie bodu
 ) je množina všetkých bodov
) je množina všetkých bodov
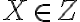 , pre ktoré platí, že úsečka
, pre ktoré platí, že úsečka
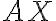 je menšia ako
je menšia ako 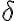 .
.
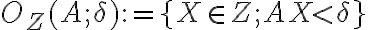
-
Nech
 je podmnožina množiny
je podmnožina množiny
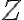 (
(
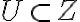 ).
Množina
).
Množina
 sa nazýva ohraničená množina, ak existuje taký bod v
sa nazýva ohraničená množina, ak existuje taký bod v
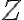 a také jeho
a také jeho 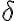 −okolie, pre ktoré platí, že
−okolie, pre ktoré platí, že
 je jeho podmnožinou.
V priloženom applete množina
je jeho podmnožinou.
V priloženom applete množina 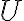 je nekonvexný 7-uholník.
je nekonvexný 7-uholník. - Nech
 je podmnožina množiny
je podmnožina množiny
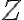 (
(
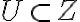 ).
Bod nazývame
).
Bod nazývame -
vnútorným bodom množiny
 , ak existuje také jeho
, ak existuje také jeho 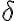 -okolie, ktoré je podmnožinou množiny
-okolie, ktoré je podmnožinou množiny
 .
. -
vonkajším bodom množiny
 , ak existuje také jeho
, ak existuje také jeho 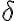 -okolie, ktorého prienik s množinou
-okolie, ktorého prienik s množinou
 je
prázdna množina.
je
prázdna množina. - hraničným bodom množiny
 , ak pre každé jeho
, ak pre každé jeho 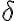 -okolie platí, že obsahuje aspoň jeden bod
množiny
-okolie platí, že obsahuje aspoň jeden bod
množiny
 a aspoň jeden bod, ktorý jej nepatrí.
a aspoň jeden bod, ktorý jej nepatrí. -
Hranica množiny
 je množinu všetkých jej hraničných bodov.
je množinu všetkých jej hraničných bodov. - Budeme hovoriť, že množina je
- uzavretá, ak každý jej hraničný bod jej patrí
- otvorená, ak aspoň jeden hraničný bod jej nepatrí.
- Dve množiny budeme nazývať neprekrývajúce sa, ak ich prienik neobsahuje žiaden vnútorný bod ani jednej z týchto množín.
Úlohy
_________________________________________________________________________________________
[1] Monoszová, G.: Planimetria - pomocný text ku prednáškam. Dostupné na: https://www.fpv.umb.sk/app/cmsFile.php?disposition=a&ID=20245
Miera (dĺžka) úsečky
- Úsečku určenú bodmi
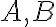 budeme označovať symbolom
budeme označovať symbolom
 . Mieru (dĺžku) úsečky
. Mieru (dĺžku) úsečky
 budeme označovať symbolom
budeme označovať symbolom
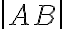 .
.
- Pri meraní a určovaní dĺžky úsečky je nutné poznať konštrukciu prenášania úsečky
 na danú polpriamku[1].
na danú polpriamku[1]. - Na určenie miery úsečky budeme potrebovať Archimedovu axiómu, ktorá je axiómou spojitosti Hilbertovho axiomatického systému.
- Vo všeobecnosti môžeme určiť dĺžku ľubovoľného jedno-rozmerného útvaru (1D). Napríklad čiara patrí do (1D), pretože na určenie bodu na nej je potrebný len jeden parameter/rozmer.
Archimedova axióma
Nech sú dané dve úsečky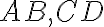 . Na polpriamke
. Na polpriamke
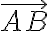 zostrojíme navzájom rôzne body
zostrojíme navzájom rôzne body
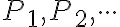 také, že
také, že
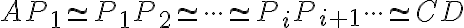 .
.
Potom existuje jediné prirodzené číslo také, že bod
také, že bod
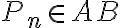 a
a
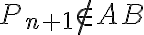 .
.
Nech sú dané dve úsečky
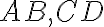 . Na polpriamke
. Na polpriamke
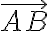 zostrojíme navzájom rôzne body
zostrojíme navzájom rôzne body
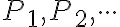 také, že
také, že
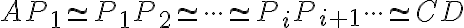 .
.
Potom existuje jediné prirodzené číslo
 také, že bod
také, že bod
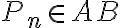 a
a
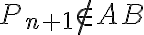 .
.
_________________________________________________________________________________________
[1] Šedivý, O., Vallo, D.: Základy elementárnej geometrie. FPV UKF v Nitre 2009, str. 9. Dostupné na internete Tu.
Určovanie dĺžky úsečky
Postup merania
-
Na polpriamku
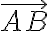 nanášame jednotkovú úsečku
nanášame jednotkovú úsečku
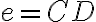 dokiaľ bude platiť
dokiaľ bude platiť
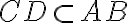 - situáciu znázorňuje applet na červenej polpriamke.
- situáciu znázorňuje applet na červenej polpriamke. - Podľa Archimedovej axiómy existuje jediné prirodzené číslo
 také, že bod
také, že bod
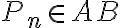 a bod
a bod
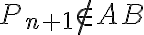 .
. - V prednastavenom applete je
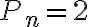 a
a 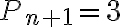
-
Veľkosť (miera) meranej úsečky
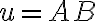 bude zdola ohraničená počtom nanesených jednotkových úsečiek a zhora to bude číslo o 1 väčšie. V applete pohybuj posuvníkom
bude zdola ohraničená počtom nanesených jednotkových úsečiek a zhora to bude číslo o 1 väčšie. V applete pohybuj posuvníkom 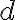 a sleduj ako sa mení ohraničenie miery úsečky
a sleduj ako sa mení ohraničenie miery úsečky
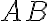 .
. - Ak chceme meranie spresniť, rozdelíme jednotkovú úsečku na 10 zhodných častí (hovoríme, že zjemňujeme jednotkovú úsečku v desiatkovej číselnej sústave). Postup uvedený pod bodom 1 opakujeme pre jednotkovú úsečku
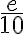 a polpriamku
a polpriamku
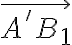 , pričom bod
, pričom bod
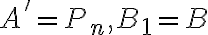 je posledný krajný bod nanášanej úsečky
je posledný krajný bod nanášanej úsečky 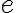 .
.
.
.
_________________________________________________________________________________________
[1] Literatúra Dostupné na: ...
Zjemnenie merania
Druhá fáza merania - zjemňovanie jednotkovej úsečky
Postup merania
-
Jednotkovú úsečku
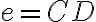 rozdelíme na 10 zhodných častí. "Nová" jednotková úsečka bude mať veľkosť
rozdelíme na 10 zhodných častí. "Nová" jednotková úsečka bude mať veľkosť
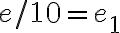 (zjemnili sme jednotkovú úsečku na desatinu).
(zjemnili sme jednotkovú úsečku na desatinu). -
Na polpriamku
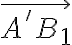 nanášame "novú" jednotkovú úsečku
nanášame "novú" jednotkovú úsečku 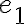 , kde bod
, kde bod
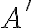 je posledný bod z predchádzajúceho merania (nanášania úsečky
je posledný bod z predchádzajúceho merania (nanášania úsečky
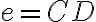 ). V prednastavenom applete je to bod označený číslicou 2. V applete je to na polpriamke v strede.
). V prednastavenom applete je to bod označený číslicou 2. V applete je to na polpriamke v strede. - Nanášame dokiaľ bude platiť
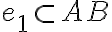 - situáciu znázorňuje applet na spodnej polpriamke. V prednastavenom applete je to bod označený desatinným číslom 2.7.
- situáciu znázorňuje applet na spodnej polpriamke. V prednastavenom applete je to bod označený desatinným číslom 2.7. - Veľkosť (miera) meranej úsečky
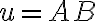 bude zdola ohraničená počtom nanesených jednotkových úsečiek plus
bude zdola ohraničená počtom nanesených jednotkových úsečiek plus 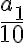 , kde
, kde 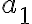 je počet nanesených nových jednotkových úsečiek
je počet nanesených nových jednotkových úsečiek 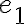 .
. - Zhora to bude číslo o
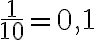 väčšie. V applete pohybuj posuvníkom
väčšie. V applete pohybuj posuvníkom 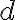 a sleduj ako sa mení ohraničenie miery úsečky
a sleduj ako sa mení ohraničenie miery úsečky
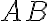 .
. - Ak chceme meranie spresniť, rozdelíme "novú" jednotkovú úsečku
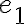 opäť na 10 zhodných častí (zjemňujeme na
opäť na 10 zhodných častí (zjemňujeme na 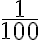 ). Postup uvedený opakujeme dovtedy, kým nedosiahneme požadovanú presnosť. Výsledkom bude zrejme reálne číslo vyjadrené desatinnom tvare.
). Postup uvedený opakujeme dovtedy, kým nedosiahneme požadovanú presnosť. Výsledkom bude zrejme reálne číslo vyjadrené desatinnom tvare.
Definícia
Ak desatinný rozvoj nájdeného reálneho čísla je
Ak desatinný rozvoj nájdeného reálneho čísla je
Príkladom dvojice nesúmerateľných úsečiek sú strana štvorca a uhlopriečka tohto štvorca.
Definícia miery úsečky
Dĺžka úsečky (veľkosť úsečky) je nezáporné reálne číslo, ktoré zisťujeme meraním.
Meranie je proces, pri ktorom porovnávame úsečku s tzv. jednotkovou úsečkou. Jednotková úsečka je úsečka, ktorej veľkosť je 1.
Miera úsečky je každé zobrazenie množiny všetkých úsečiek do množiny všetkých nezáporných reálnych čísel s vlastnosťami, ktoré sú uvedené v nasledovnom odseku.
všetkých úsečiek do množiny všetkých nezáporných reálnych čísel s vlastnosťami, ktoré sú uvedené v nasledovnom odseku.
Meranie je proces, pri ktorom porovnávame úsečku s tzv. jednotkovou úsečkou. Jednotková úsečka je úsečka, ktorej veľkosť je 1.
Miera úsečky je každé zobrazenie množiny
 všetkých úsečiek do množiny všetkých nezáporných reálnych čísel s vlastnosťami, ktoré sú uvedené v nasledovnom odseku.
všetkých úsečiek do množiny všetkých nezáporných reálnych čísel s vlastnosťami, ktoré sú uvedené v nasledovnom odseku.
Definícia - miera/dĺžka úsečky
Nech je množina všetkých úsečiek. Funkciu, ktorá má nasledujúce tri vlastnosti
je množina všetkých úsečiek. Funkciu, ktorá má nasledujúce tri vlastnosti
Nech
 je množina všetkých úsečiek. Funkciu, ktorá má nasledujúce tri vlastnosti
je množina všetkých úsečiek. Funkciu, ktorá má nasledujúce tri vlastnosti
Poznámky
- Z definície a prvej vlastnosti vyplýva, že každej úsečke prislúcha jediné kladné číslo, ktoré je jej dĺžkou.
- Dĺžka úsečky nezávisí od jej polohy.
- Jednotková úsečka má dĺžku 1.
Definície - vzdialenosť dvoch útvarov
Cvičenia.
- Je daná úsečka
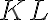 . Zostrojte trojuholník
. Zostrojte trojuholník
 , ktorého strany majú veľkosť:
, ktorého strany majú veľkosť:
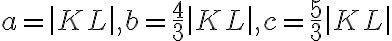 .
Úlohu vyriešte v Euklidovskej rovine.
.
Úlohu vyriešte v Euklidovskej rovine.
Návod: Najskôr úsečku rozdeľte na 3 rovnaké časti. - Je daná úsečka
 . Zostrojte trojuholník
. Zostrojte trojuholník
 , ktorého strany majú veľkosť:
, ktorého strany majú veľkosť:
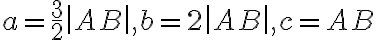 .
Úlohu vyriešte v Poincare Disc.
.
Úlohu vyriešte v Poincare Disc.
Návod: Najskôr úsečku rozdeľte na 2 rovnaké časti.
Miera v Poincare Disku
Nech
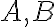 sú ľubovoľné dva body patriace Poincare Disc. Hyperbolickú hPriamku
sú ľubovoľné dva body patriace Poincare Disc. Hyperbolickú hPriamku označíme
označíme 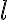 a "nevlastné" koncové body tejto priamky pomocou
a "nevlastné" koncové body tejto priamky pomocou
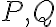 .
.
Tieto body pomenujeme tak, aby platilo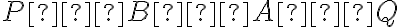 .
.
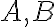 sú ľubovoľné dva body patriace Poincare Disc. Hyperbolickú hPriamku
sú ľubovoľné dva body patriace Poincare Disc. Hyperbolickú hPriamku označíme
označíme 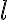 a "nevlastné" koncové body tejto priamky pomocou
a "nevlastné" koncové body tejto priamky pomocou
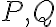 .
.
Tieto body pomenujeme tak, aby platilo
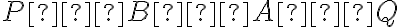 .
.
Nech A, B, P, Q sú navzájom rôzne kolineárne body také, že platí
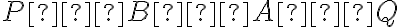 .
.
Dvojpomer usporiadanej štvorice bodov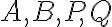 je podiel deliacich pomerov
je podiel deliacich pomerov
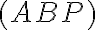 a
a
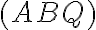 ; (dvojpomer takejto štvorice bodov
; (dvojpomer takejto štvorice bodov
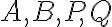 označujeme
označujeme
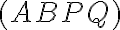 ).
).
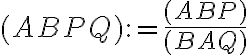
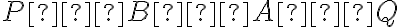 .
.
Dvojpomer usporiadanej štvorice bodov
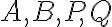 je podiel deliacich pomerov
je podiel deliacich pomerov
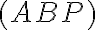 a
a
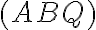 ; (dvojpomer takejto štvorice bodov
; (dvojpomer takejto štvorice bodov
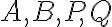 označujeme
označujeme
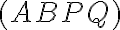 ).
).
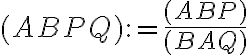
Príklad
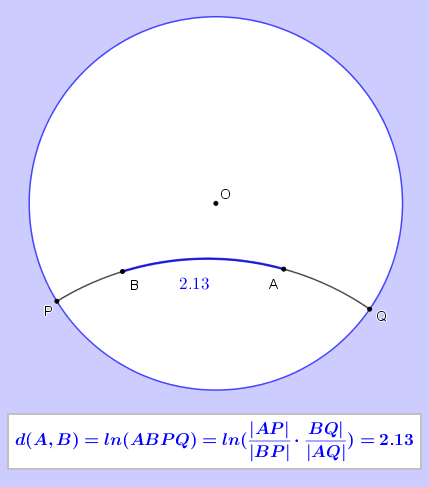 Otvorte applet Tu
Otvorte applet Tu
Úlohy
Miera rovinného útvaru
Rovinný útvar, ktorý je ohraničený a jeho hranica je jednorozmerný útvar sa nazýva merateľný útvar.
Množinu všetkých merateľných útvarov budeme označovať symbolom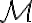 .
.
Množinu všetkých merateľných útvarov budeme označovať symbolom
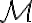 .
.
_________________________________________________________________________________________
[1] Literatúra Dostupné na: ...
Jadro a obal útvaru
Štvorcová sieť
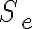 v euklidovskej rovine je systém navzájom rovnobežných priamok
v euklidovskej rovine je systém navzájom rovnobežných priamok 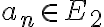 a kolmých priamok
a kolmých priamok 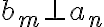 .
.
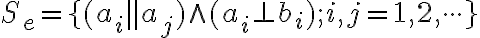 ,
,
pričom platí, že vzdialenosť navzájom rovnobežných priamok je rovná veľkosti úsečky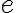 . Rozmer štvorcovej siete je číslo
. Rozmer štvorcovej siete je číslo  .
.
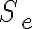 v euklidovskej rovine je systém navzájom rovnobežných priamok
v euklidovskej rovine je systém navzájom rovnobežných priamok 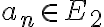 a kolmých priamok
a kolmých priamok 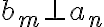 .
.
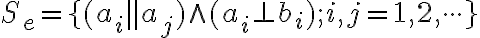 ,
,
pričom platí, že vzdialenosť navzájom rovnobežných priamok je rovná veľkosti úsečky
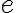 . Rozmer štvorcovej siete je číslo
. Rozmer štvorcovej siete je číslo  .
.
 Otvor applet Tu
Otvor applet Tu Jordanova teória miery
Otvor Tu
Postup určenia obsahu útvaru
Pomocou Jordanovej metódy môžeme odhadnúť obsah ohraničeného útvaru  tak, že ho vhodne umiestnime do štvorcovej siete.
tak, že ho vhodne umiestnime do štvorcovej siete.
 tak, že ho vhodne umiestnime do štvorcovej siete.
tak, že ho vhodne umiestnime do štvorcovej siete.
V prvom kroku merania (určovania obsahu útvaru) si zvolíme štvorcovú sieť
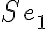 s rozmerom
s rozmerom 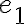 . (Napríklad
. (Napríklad 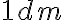 ).
).
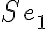 s rozmerom
s rozmerom 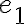 . (Napríklad
. (Napríklad 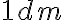 ).
).
- Jednotka miery je štvorec
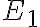 so stranou
so stranou 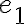 a podľa dohovoru pre jeho veľkosť/obsah
a podľa dohovoru pre jeho veľkosť/obsah
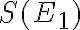 platí
platí
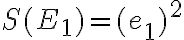 .
. - Určíme všetky štvorce, ktoré patria do jadra
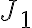
- Nech
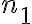 je počet štvorcov siete, ktoré patria do jadra útvaru, potom pre obsah jadra útvaru platí
je počet štvorcov siete, ktoré patria do jadra útvaru, potom pre obsah jadra útvaru platí
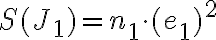
čo predstavuje dolný odhad obsahu meraného útvaru. - Podobne postupujeme pri určovaní obsahu obalu. Spočítame všetky štvorce, ktoré patria obalu
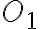 meraného útvaru
meraného útvaru  .
.
- Nech
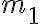 je počet štvorcov siete, ktoré patria do obalu útvaru, potom pre obsah jadra útvaru platí
je počet štvorcov siete, ktoré patria do obalu útvaru, potom pre obsah jadra útvaru platí
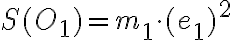
čo predstavuje horný odhad obsahu meraného útvaru. - Po prvom meraní dôjdeme k záveru, že pre obsah
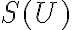 útvaru
útvaru  platí
platí
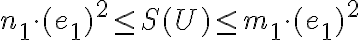
čo predstavuje dolný odhad obsahu meraného útvaru. Ak nám takýto odhad nestačí, zjemníme štvorcovú sieť.
V druhom kroku merania zvolíme menšiu jednotkovú úsečku 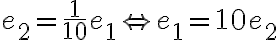 . (Napríklad
. (Napríklad 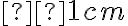 ).
).
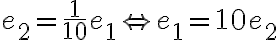 . (Napríklad
. (Napríklad 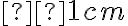 ).
).
- Teraz jednotka miery je štvorec
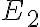 , ktorý má 100 násobne menší obsah ako štvorec
, ktorý má 100 násobne menší obsah ako štvorec 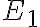 . Pre jeho obsah platí
. Pre jeho obsah platí
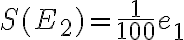 .
.
- Zrejme platí, že každý štvorec z jadra
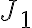 obsahuje 100 menších štvorcov zjemnenej štvorcovej siete.
obsahuje 100 menších štvorcov zjemnenej štvorcovej siete. - Tieto menšie štvorce určite patria do jadra
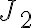 , ktoré bolo vytvorené v zjemnenej sieti. Preto platí
, ktoré bolo vytvorené v zjemnenej sieti. Preto platí
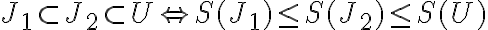
- Analogické vzťahy platia aj pre obsah obalu:
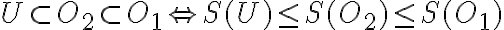 .
. - Z predchádzajúcich vzťahov a po
 krokoch zjemňovania siete dostaneme
krokoch zjemňovania siete dostaneme
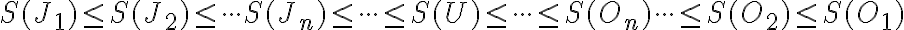 .
.
Potom
zrejme postupnosť
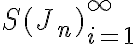 je neklesajúca, zhora ohraničená a postupnosť
je neklesajúca, zhora ohraničená a postupnosť
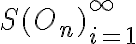 je
nerastúca, zdola ohraničená.
Členy postupnosti
je
nerastúca, zdola ohraničená.
Členy postupnosti
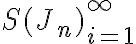 sú dolné ohraničenia a členy postupnosti
sú dolné ohraničenia a členy postupnosti
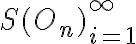 sú horné
ohraničenia veľkosti útvaru
sú horné
ohraničenia veľkosti útvaru  a limity týchto postupností sa rovnajú hodnote
a limity týchto postupností sa rovnajú hodnote 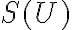 .
.
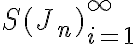 je neklesajúca, zhora ohraničená a postupnosť
je neklesajúca, zhora ohraničená a postupnosť
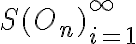 je
nerastúca, zdola ohraničená.
Členy postupnosti
je
nerastúca, zdola ohraničená.
Členy postupnosti
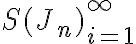 sú dolné ohraničenia a členy postupnosti
sú dolné ohraničenia a členy postupnosti
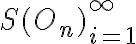 sú horné
ohraničenia veľkosti útvaru
sú horné
ohraničenia veľkosti útvaru  a limity týchto postupností sa rovnajú hodnote
a limity týchto postupností sa rovnajú hodnote 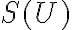 .
.
Seminárne cvičenie
Riešte úlohy
- Dané sú rôzne body
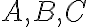 . Určte množinu (šrafovaním)
. Určte množinu (šrafovaním)
- Je daná úsečka
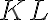 .
.
-
Zostrojte trojuholník
 , ktorého strany majú veľkosť:
, ktorého strany majú veľkosť:
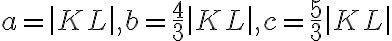 .
Úlohu vyriešte v Euklidovskej rovine.
.
Úlohu vyriešte v Euklidovskej rovine.
Návod: Najskôr úsečku rozdeľte na 3 rovnaké časti. - Je daná úsečka
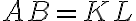 . Zostrojte trojuholník
. Zostrojte trojuholník
 , ktorého strany majú veľkosť:
, ktorého strany majú veľkosť:
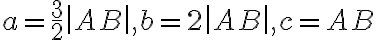 .
Úlohu vyriešte v Poincare Disku.
.
Úlohu vyriešte v Poincare Disku.
Návod: Najskôr úsečku rozdeľte na 2 rovnaké časti. - Je daná úsečka
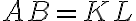 . Zostrojte trojuholník
. Zostrojte trojuholník  , ktorého strany majú veľkosť:
, ktorého strany majú veľkosť: 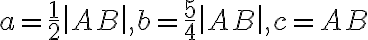 . Úlohu vyriešte v Poincare Disku.
. Úlohu vyriešte v Poincare Disku.
-
Zostrojte trojuholník
- Daný je pravidelný 6-uholník
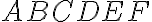 so stredom
so stredom
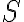 a ďalej sú dané body
a ďalej sú dané body
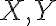 , pričom bod
, pričom bod
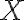 leží na polpriamke
leží na polpriamke
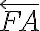 a zároveň platí
a zároveň platí
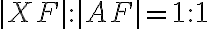 . Bod
. Bod
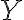 leží na polpriamke
leží na polpriamke
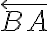 a zároveň platí
a zároveň platí
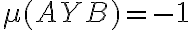 . Určte vzdialenosti
. Určte vzdialenosti
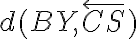
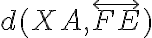
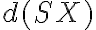
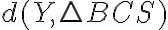
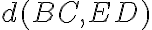 Zadanie otvorte Tu
Zadanie otvorte Tu
- a. Daný je trojuholník
 a body
a body
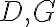 tak, že bod
tak, že bod
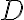 je stred strany
je stred strany
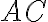 a
a
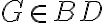 , pričom
, pričom 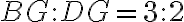 . Určte obsahy všetkých troch neprekrývajúcich sa častí, na ktoré je trojuholník
. Určte obsahy všetkých troch neprekrývajúcich sa častí, na ktoré je trojuholník
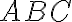 rozdelený (otvorte si zadanie), ak pre obsah trojuholníka platí
rozdelený (otvorte si zadanie), ak pre obsah trojuholníka platí
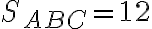 .
.
Zadanie otvorte Tu .
b. Daný je trojuholník a body
a body 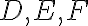 také, že
také, že 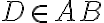 ,
, 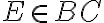 a
a 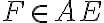 , pričom
, pričom 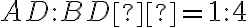 ,
, 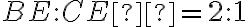 a
a 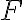 je stred strany
je stred strany 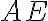 . Určte obsahy všetkých štyroch vyznačených neprekrývajúcich sa častí, na ktoré je trojuholník
. Určte obsahy všetkých štyroch vyznačených neprekrývajúcich sa častí, na ktoré je trojuholník 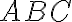 rozdelený (otvorte si zadanie), ak pre obsah trojuholníka platí
rozdelený (otvorte si zadanie), ak pre obsah trojuholníka platí 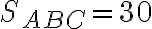 .
.
Zadanie otvorte Tu . - Daný je pravidelný 6-uholník
 s jednotkovým obsahom. Určte obsahy jednotlivých neprekrývajúcich sa útvarov, na ktoré je šesťuholník rozdelený. (Dané sú dve rozdelenia. Riešte pre každé rozdelenie samostatne.)
s jednotkovým obsahom. Určte obsahy jednotlivých neprekrývajúcich sa útvarov, na ktoré je šesťuholník rozdelený. (Dané sú dve rozdelenia. Riešte pre každé rozdelenie samostatne.)
Zadanie otvorte Tu - Rozdeľte obdĺžnik na 4 neprekrývajúce sa trojuholníky, ktorých obsahy tvoria
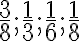 z obsahu obdĺžnika.
z obsahu obdĺžnika.
- Odvoďte vzťah pre výpočet obsahu rovnostranného trojuholníka, ak je daný a) polomer
 jemu opísanej kružnice, b) polomer
jemu opísanej kružnice, b) polomer 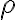 jemu vpísanej kružnice.
jemu vpísanej kružnice.
- Odvoďte vzťah pre výpočet obsahu pravidelného 6-uholníka, ak je daný a) polomer
 jemu opísanej kružnice, b) polomer
jemu opísanej kružnice, b) polomer 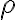 jemu vpísanej kružnice.
jemu vpísanej kružnice.
- Vypočítajte obsah štvoruholníka, zadanie Tu.
- Vypočítajte obsah päťuholníka, zadanie Tu.