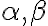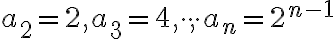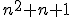Problém verzus úloha
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Problém verzus úloha |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:24 |
Úvod
Rozdiel medzi problémom a úlohou nie je v literatúre jednoznačne vymedzený. Rozdiely chápeme hlavne medzi postupom riešenia daného problému resp. úlohy. Úlohu môžeme chápať ako jednu časť pri riešení problému, pri ktorej vieme stanoviť spôsob riešenia a zároveň poznáme spôsob prechodu medzi týmito časťami k dosiahnutiu cieľa. Pre lepšie pochopenie tohto rozdielu uvedieme definície z práce1) profesora Gahéra.
- Riešiteľ má problém, keď je situácia v jednom stave, riešiteľ chce, aby situácia bola v inom stave a riešiteľ nepozná zreteľný spôsob eliminovania prekážky medzi dvomi stavmi.
- Problematická situácia sa zásadne odlišuje od neproblematickej
- v neproblematickej situácii (pri riešení úlohy) sa opierame o známe a schémy a postupy pri dosiahnutí cieľa
- v problematickej situácii (riešenie problému) musíme počítať s neznámymi postupmi, nejasným vývojom a musíme hľadať celkom novú a zatiaľ neznámu cestu k dosiahnutiu cieľa.
- V problematickej situácii sa riešiteľ snaží nájsť spôsob, ako transformovať problematickú situáciu na neproblematickú. Do tejto kategórie zaraďujeme aj dokazovanie tvrdení resp. dôvodenie.
Vyriešiť úlohu nie je to isté, ako riešiť problém
- Na splnenie úlohy používame známe a ovládané metódy (s definitívnou alebo určitou prediktívnou istotou).
- Na riešenie problému používame vedeckú metódu, ktorá vyžaduje presne vymedzené definície, poznatky, stanovenie hypotéz, ich dôkazy. Metóda je spôsob ako vyriešiť úlohu, je to spôsob (dokonca návod) na dosiahnutia určitých výsledkov pri riešení problému.
Cvičenie.
Vypracujte rešerš práce Vypracujte rešerš práce1) profesora Gahéra.
Vypracujte rešerš práce Vypracujte rešerš práce1) profesora Gahéra.
___________________________________________________________________________
1) Gahér, F.,Marko, V.: Metóda, problém a úloha. FF UK Bratislava 2017. Dostupné na Tu.
1) Gahér, F.,Marko, V.: Metóda, problém a úloha. FF UK Bratislava 2017. Dostupné na Tu.
Úlohy s viacerými riešeniami
Významnou zložkou rozvoja osobnosti žiaka je jeho aktívne zapojenie do vyučovacieho procesu. Aktívna činnosť žiaka na matematickom vzdelávaní sa uskutočňuje hlavne prostredníctvom riešenia rozličných matematických úloh. Podľa M. Cirjaka1)
Aktívna činnosť žiakov pri riešení úloh je základným problémom didaktiky matematiky.
Pri riešení úloh musíme mať na zreteli dve skutočnosti. Prvá spočíva v tom koľko úloh vyriešime (kvantitatívna zložka) a druhá je determinovaná tým ako úlohy vyriešime (kvalitatívna). V spomínanej práci1) sa uvádza:
Pre rozvoj matematického myslenia je užitočnejšie vyriešiť jednu úlohu viacerými spôsobmi, ako viacej úloh toho istého typu jedným spôsobom, ktorý je iba rutinným napodobňovaním predloženého vzoru.
Z predností zaraďovania úloh s viacerými spôsobmi riešenia vyberáme
- umožňujú komplexný pohľad na matematiku a na vzájomné súvislosti medzi rôznymi tematickými okruhmi
- vytvárajú u žiakov potrebu objavovať, hľadať efektívnejšie postupy
- rozširuje možnosti aplikácie matematiky.
_____________________________________________________
1) Cirjak, M.: Zbierka divergentných a iných neštandardných úloh (Tvorivosť v matematike). Essox, Prešov 2000.
1) Cirjak, M.: Zbierka divergentných a iných neštandardných úloh (Tvorivosť v matematike). Essox, Prešov 2000.
Trojuholník s daným obvodom
Riešenia tejto úlohy je možné rozdeliť napríklad do piatich skupín.
- Riešenie vychádza z analytického rozboru, v ktorom sa využijú základné planimetrické vlastnosti. V tomto prípade je možné využiť vlastnosť vonkajšieho uhla trojuholníka a zhodnosť uhlov pri základni rovnoramenného trojuholníka.
- Ďalšie riešenie je s využitím podobnosti (rovnoľahlosti) trojuholníkov. Má charakter induktívny.
- Tretie riešenie má charakter typicky konštruktívny, pri ktorom sa využíva pomocný trojuholník.
- Štvrté riešenie využíva vlastnosti pripísaných kružníc k trojuholníku. Doplňujúci študijný text nájdete na konci tejto strány.
- Piate riešenie využíva zhodné zobrazenie (posunutie
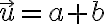 ) a deduktívne uvažovanie.
) a deduktívne uvažovanie.
K tejto úlohe odporúčame preštudovať materiál o pripísaných kružniciach k trojuholníku. Je spracovaný vo forme appletu Text 1 Tu a Text 2 Tu.
Riešenie
- Prvé riešenie vychádza z analytického rozboru. Pokúste sa o takéto riešenie.
Rozbor Tu
- Druhé riešenie má charakter induktívny, vyriešte úlohu s využitím podobnosti (rovnoľahlosti).
- Tretie riešenie má charakter typicky konštruktívny, pri ktorom sa využíva pomocný trojuholník.
Riešenie Tu
- Štvrté riešenie využíva vlastnosti pripísaných kružníc k trojuholníku. Doplňujúci študijný text nájdete na konci tejto strány.
Riešenie Tu
- Piate riešenie využíva zhodné zobrazenie (posunutie) a deduktívne uvažovanie.
Riešenie Tu
K tejto úlohe odporúčame preštudovať materiál o pripísaných kružniciach k trojuholníku. Je spracovaný vo forme appletu Text 1 Tu a Text 2 Tu.
Analytické a syntetické riešenie
V tejto kapitole uvedieme niektoré základné pojmy, ktoré je nutné zadefinovať k problematike riešenia úloh a riešenia problémov. Zameriame sa hlavne na tri najčastejšie spôsoby/metódy pri riešení úloh.
- Analytické riešenie
- Syntetické riešenie
- Numerické resp. približné riešenie
- Algebraické riešenie
- Pri analytickom1) riešení začíname rozborom úlohy, zistíme ktoré údaje sú neznáme a či máme dostatok daných údajov na zistenie neznámych. Výsledkom rozboru je matematizácia. Analytické riešenie je v matematike hľadanie riešenia pomocou známych vzťahov a postupných úprav. Analytické riešenie alebo uzavreté riešenie sa niekedy označuje ako explicitné riešenie.
- Syntetické riešenie spočíva v tom, že úlohu rozkladáme na niekoľko jednoduchých úloh a vypočítame ich. Ak sme všetko vypočítali, čo z daných údajov je možné vypočítať, alebo čo považujeme za potrebné. Nakoniec urobíme syntézu, teda zhrnieme tie výpočty, ktoré vedú k riešeniu.
- Numerické riešenie je hľadanie približného riešenia pomocou vhodnej numerickej metódy. Používa sa zvyčajne, keď nájdenie presného analytického riešenia je veľmi komplikované alebo nemožné.
- Pri algebraickom riešení sa často využíva metóda, ktorá využíva formálne postupy pri riešení rovníc. Pri riešení sa opierame o definície, matematické vety a vzorce, ktoré nám umožňujú vytvárať algoritmy riešení. S výhodou sa používa grafické znázornenie pomocou vhodného softvéru.
Pri riešení akéhokoľvek typu matematickej úlohy sa dnes vo veľkej miere využíva počítačová simulácia pomocou inteligentných softvérov (Maple, GeoGebra a pod.),
ktoré sú navrhnuté tak, aby predpovedali správanie alebo výsledok skutočného alebo fyzického systému.
___________________________________________________________________________
1) Žídek, O.: Primárne matematické vzdelávanie 2. Interaktívna elektronická učebnica PFTU Trnava 2013. Dostupné Tu.
1) Žídek, O.: Primárne matematické vzdelávanie 2. Interaktívna elektronická učebnica PFTU Trnava 2013. Dostupné Tu.
Rovnostranný trojuholník
Úloha
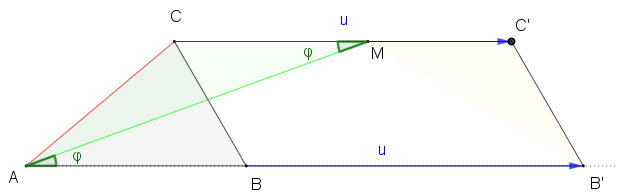
Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Larson, Príklad 8.1.16 1)
Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Larson, Príklad 8.1.16 1)
Úlohu vyriešte tromi spôsobmi:
Geometrické modelovanie - riešenie pomocou GeoGebry vhodné pre základné školy
Konštrukčné riešenie - uplatňuje sa induktívne myslenie, využite nejaké zhodné zobrazenie
Algebraické riešenie - pomocou kosínusovej vety, riešenie vhodné pre stredné školy
Geometrické modelovanie - riešenie pomocou GeoGebry vhodné pre základné školy
Konštrukčné riešenie - uplatňuje sa induktívne myslenie, využite nejaké zhodné zobrazenie
Algebraické riešenie - pomocou kosínusovej vety, riešenie vhodné pre stredné školy
___________________________________________________________________________
1) Larson, C., L.: Problem-Solving Through Problems. S pringer-Verlag 1983. Príklad 8.1.16. Dostupné Tu.
1) Larson, C., L.: Problem-Solving Through Problems. S pringer-Verlag 1983. Príklad 8.1.16. Dostupné Tu.
Riešenie
Úloha
Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Larson, Príklad 8.1.16 1)
Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Larson, Príklad 8.1.16 1)
Geometrické modelovanie/riešenie pomocou GeoGebry vhodné pre základné školy
Konštrukčné riešenie - uplatňuje sa induktívne myslenie
Algebraické riešenie pomocou kosínusovej vety vhodné pre stredné školy
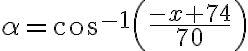
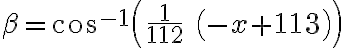
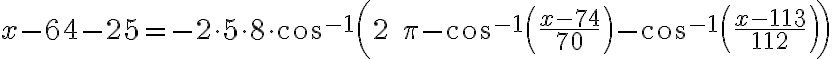
Pozrite si riešenie v GeoGebre Tu.
Konštrukčné riešenie - uplatňuje sa induktívne myslenie
Algebraické riešenie pomocou kosínusovej vety vhodné pre stredné školy
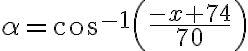
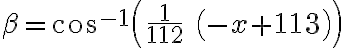
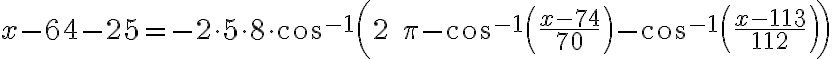
Pozrite si riešenie v GeoGebre Tu.
___________________________________________________________________________
1) Larson, C., L.: Problem-Solving Through Problems. S pringer-Verlag 1983. Príklad 8.1.16. Dostupné Tu.
1) Larson, C., L.: Problem-Solving Through Problems. S pringer-Verlag 1983. Príklad 8.1.16. Dostupné Tu.
Dôvodenie a dokazovanie
Pri riešení problémov sa stretávame s potrebou zdôvodniť resp. dokázať naše čiastkové tvrdenia. Pri zdôvodňovaní sa opierame o už dokázané platné tvrdenia (matematické vety).
Zdôvodňovanie je procesom argumentácie.
Definícia - Dôvodenie a argumentácia.
Proces komunikácie s ostatnými alebo so sebou samým, ktorý umožňuje odvodzovať matematické výroky z iných matematických výrokov. (Jeannotte & Kieran, 2017, s. 9).
„Lepidlo“, ktoré pomáha matematike dávať zmysel (https://nrich.maths.org/10990).
Proces komunikácie s ostatnými alebo so sebou samým, ktorý umožňuje odvodzovať matematické výroky z iných matematických výrokov. (Jeannotte & Kieran, 2017, s. 9).
„Lepidlo“, ktoré pomáha matematike dávať zmysel (https://nrich.maths.org/10990).
Definícia - Argument.
Argument je nástroj vďaka ktorému z počiatočných dát využitím legitímnych krokov prichádzame k tvrdeniu (Toulmin, 2003).
Argument je nástroj vďaka ktorému z počiatočných dát využitím legitímnych krokov prichádzame k tvrdeniu (Toulmin, 2003).
Legitímne kroky zahŕňajú:
Reprezentácie argumentov
- Grafická (špecifický vs. všeobecný obrázok).
- Symbolická (konkrétne vs. všeobecné vyjadrenie).
- Verbálna (slovný vs. písomný opis).
- Fyzické objekty, digitálne nástroje.
Cvičenie.
- Viete len z obrázku zistiť/určiť odpovedajúce tvrdenie?
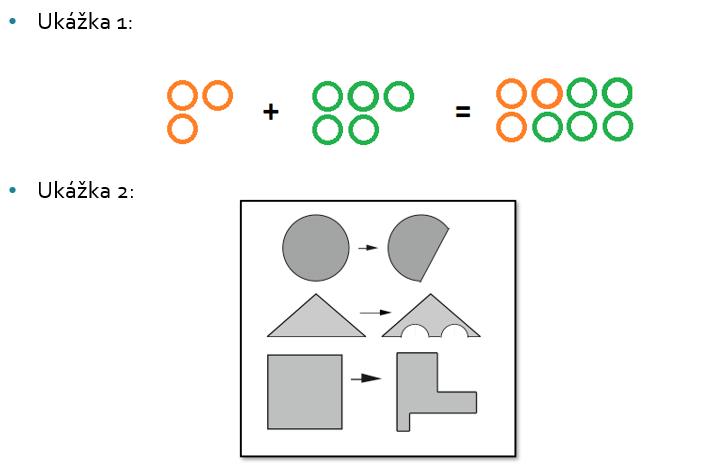
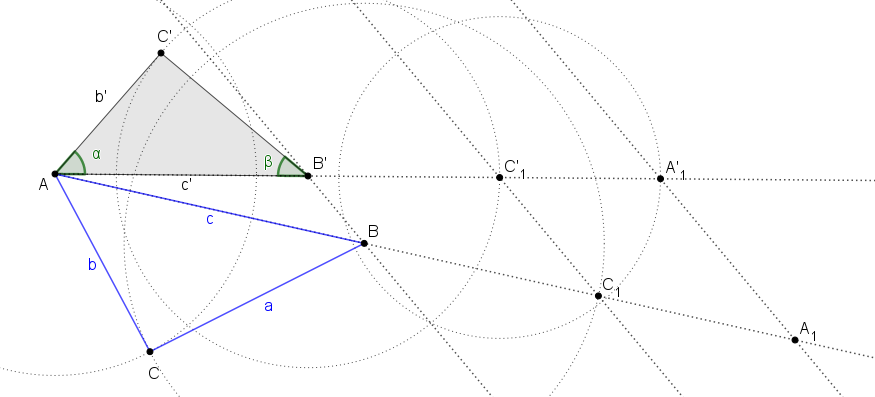
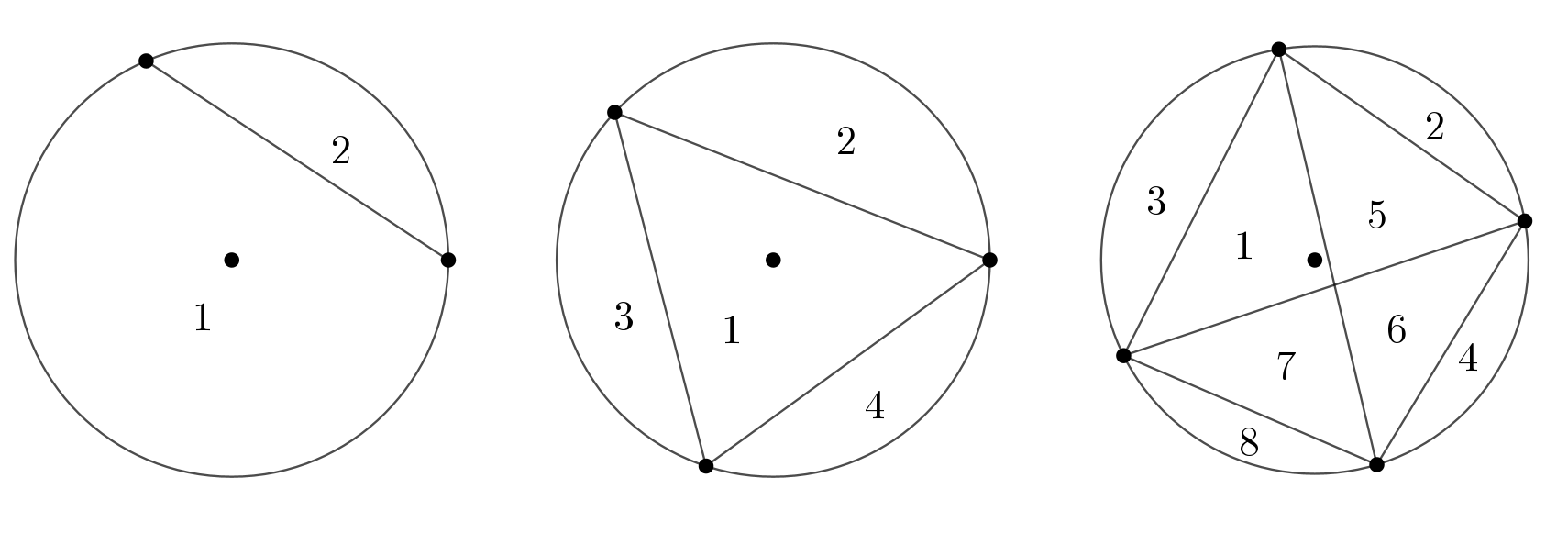
- Overte platnosť tvrdenia "Súčet ľubovoľných troch po sebe idúcich čísel sa rovná trojnásobku prostredného čísla." Graficky pomocou trojuholníkových čísel, pomocou matematickej symboliky pre postupnosti.
- S použitím optimálneho/minimálneho počtu slov slovne/písomne dokážte tvrdenia:
- Súčet dvoch nepárnych čisel je párne číslo.
- Prvočísel je nekonečne veľa.
Poznámky.
- Dôvody argumentácie na hodinách matematiky:
- ukázať fungovanie pravidla (prečo pravidlo funguje?),
- overenie platnosti pravidla/tvrdenia,
- systematizáciou argumentov sa dopracovať k dôkazu.
- Prečo argumentovať:
- zvýšenie porozumenia,
- motivácia,
- komunikačné zručnosti (formulácia, ujasnenie/vysvetlenie).
Argumentácia je jednou z neoddeliteľných súčastí matematickej zručnosti (Kilpatrick, 2011).