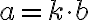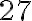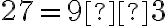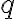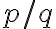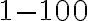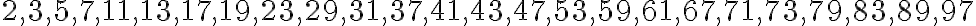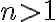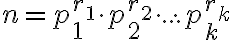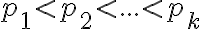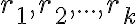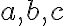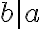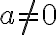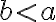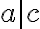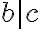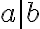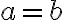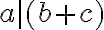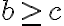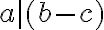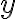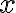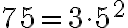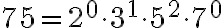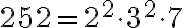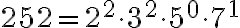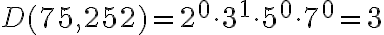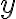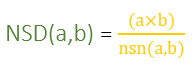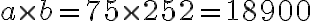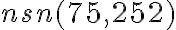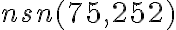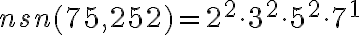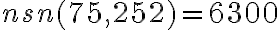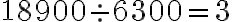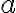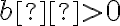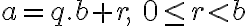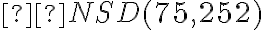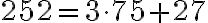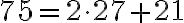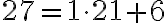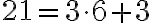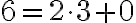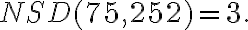Základná veta aritmetiky
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Základná veta aritmetiky |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:39 |
1. Úvod
Aritmetika (z gréckeho slova arithmós - číslo) je odbor matematiky, ktorý študuje čísla, ich vzťahy a vlastnosti. Predmetom aritmetiky je pojem číslo (prirodzené, celé, racionálne, reálne a komplexné číslo) a jeho vlastnosti. Aritmetika sa zaoberá meraniami, operáciami s číslami. Aritmetika je najstaršia zo základných matematických vied, úzko súvisí s algebrou, geometriou a teóriou čísel.
Za základné aritmetické operácie považujeme: sčítanie, odčítanie, násobenie a delenie. Aritmetika sa taktiež zaoberá počítaním s percentami, mocninami a odmocninami, exponenciálnymi a logaritmickými funkciami.
2. Dejiny
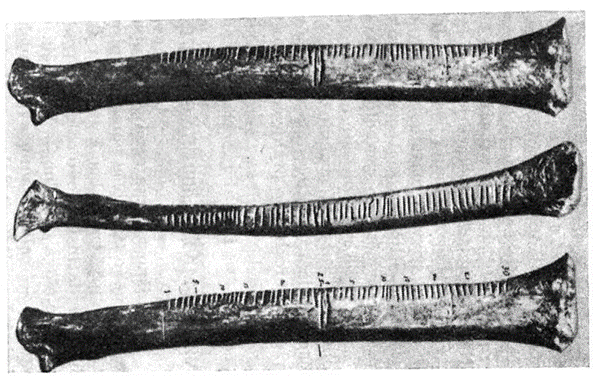
Archeologické vykopávky potvrdzujú, že človek vytvoril prvé aritmetické pojmy už v dobe kamennej. Za prvý dôkaz, že človek už vedel počítať sa považujú vrubovky.
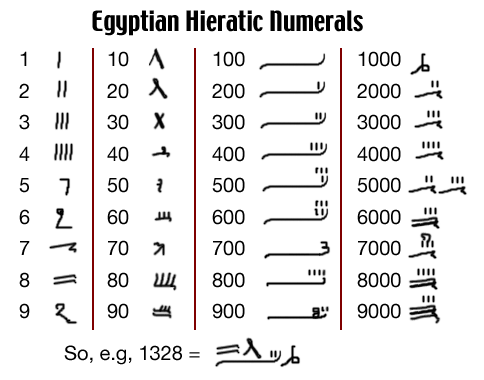 číselná sústava - Egypt
číselná sústava - Egypt  číselná sústava - Babylon
číselná sústava - Babylon
 rímske čislice
rímske čislice rímske počítadlo - abakus
rímske počítadlo - abakus
...


Aritmetika sa vyvíjala v Indii a krajinách islamu, odkiaľ najnovšie úspechy tej doby v oblasti matematického myslenia prenikli do západnej Európy. Vyvinuli pozičný číselný zápis a zaviedli symbol pre nulu. V siedmom storočí zaviedol matematik Brahmaputra používanie nuly ako samostatného čísla a určil výsledky pre všetky operácie s nulou okrem výsledku delenia nulou. Bolo zavedených 9 arabských číslic, ktoré práve Leonardo Pisánsky rozšíril do celej Európy prostredníctvom svojej knihy Liber Abaci v roku 1202. Napísal: "metóda Indov prevyšuje akúkoľvek známu metódu výpočtov. Je to úžasná metóda, pomocou ktorej sú robené výpočty pomocou deviatich číslic a symbolu nula."
 Leonardo Pisánsky
Leonardo Pisánsky ukážka z knihy Liber Abaci
K axiometrickému vybudovaniu aritmetiky dochádza až v 19. storočí. Na Bolzanovom pojme množín, vybudoval Georg Cantor teóriu kardinálnych a ordinálnych čísel. Na začiatku 20. storočia Ernst Zermelo publikoval axiomatiku teórie množín, ktorá sa stala okrem iného aj základom pri výstavbe aritmetiky.
3. Základná veta aritmetiky
 aspoň jedného ďalšieho spoločného deliteľa.
aspoň jedného ďalšieho spoločného deliteľa.Napríklad: Čísla
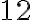 a
a 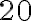 sú súdeliteľné, lebo majú deliteľov
sú súdeliteľné, lebo majú deliteľov 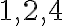 .
.Nesúdeliteľné čísla sú čísla, ktoré nemajú okrem čísla
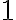 žiadneho spoločného deliteľa.
žiadneho spoločného deliteľa. Napríklad: Čísla
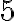 a
a 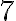 sú nesúdeliteľné, lebo majú len jedného spoločného deliteľa -
sú nesúdeliteľné, lebo majú len jedného spoločného deliteľa - 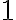 .
.Vyjadrenie zloženého čísla súčinom jeho deliteľov väčších ako 1 nazývame rozklad zloženého čísla.
To isté číslo môže mať rôzne rozklady.
Napríklad:
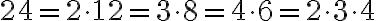
Veta: Každé zložené číslo
 je deliteľné aspoň jedným prvočíslom
je deliteľné aspoň jedným prvočíslom  , pre ktoré platí
, pre ktoré platí 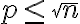 .
.Ak zistíme, že číslo
 nie je deliteľné nijakým prvočíslom
nie je deliteľné nijakým prvočíslom  , pre ktoré platí
, pre ktoré platí 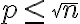 , tak
, tak  je prvočíslo.
je prvočíslo.
Uveďme si niektoré spôsoby, ktorými zaznamenávame postup na prvočíselný rozklad.
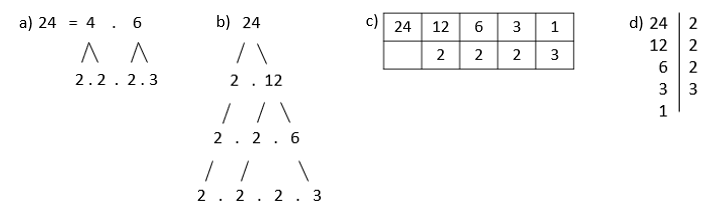
4. Vlastnosti a kritériá deliteľnosti
 , ak je posledná číslica párna, alebo je na poslednom mieste číslica
, ak je posledná číslica párna, alebo je na poslednom mieste číslica 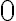
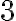 , ak je ciferný súčet deliteľný
, ak je ciferný súčet deliteľný 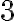
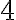 , ak je posledné dvojčíslie deliteľné
, ak je posledné dvojčíslie deliteľné 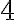
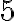 , ak je na poslednom mieste
, ak je na poslednom mieste 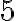 alebo
alebo 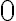
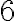 , ak je číslo deliteľné
, ak je číslo deliteľné 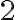 a súčasne aj
a súčasne aj 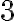
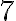 , ak je siedmimi deliteľný súčet vypočítaný tak, že sa prvá až n-tá číslica odzadu vynásobí postupne číslami (periodicky sa opakujúcimi):
, ak je siedmimi deliteľný súčet vypočítaný tak, že sa prvá až n-tá číslica odzadu vynásobí postupne číslami (periodicky sa opakujúcimi): 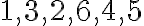
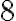 , ak je posledné trojčíslie deliteľné
, ak je posledné trojčíslie deliteľné 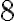
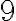 , ak je ciferný súčet deliteľný
, ak je ciferný súčet deliteľný 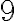
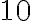 , ak je na poslednom mieste
, ak je na poslednom mieste 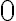
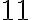 , ak je rozdiel súčtu číslic na nepárnom a párnom mieste deliteľný
, ak je rozdiel súčtu číslic na nepárnom a párnom mieste deliteľný 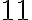
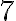 : Je
: Je 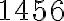 deliteľné
deliteľné 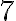 ?
?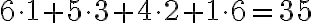 (číslo deliteľné
(číslo deliteľné 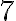 ).
).Príklad pre deliteľnosť
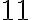 : Je číslo
: Je číslo 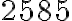 deliteľné
deliteľné 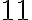 ?
?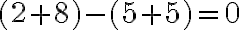 (číslo deliteľné
(číslo deliteľné 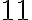 ).
).4.1. Príklady
- Zisti, ktoré z čísel
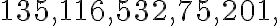 alebo
alebo 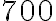 , je deliteľné
, je deliteľné 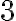 alebo
alebo 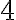 .
. - Zisti, ktoré z čísel
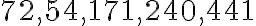 alebo
alebo 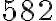 , je deliteľné
, je deliteľné 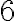 alebo
alebo 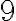 .
. - Ktorým číslom z prvej desiatky nie je deliteľné číslo
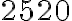 ? Využi na riešenie znaky deliteľnosti.
? Využi na riešenie znaky deliteľnosti. - V zápise čísla
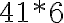 nahraď hviezdičku takou číslicou, aby ste dostali číslo deliteľné: a) tromi, b) štyrmi, c) šiestimi, d) deviatimi.
nahraď hviezdičku takou číslicou, aby ste dostali číslo deliteľné: a) tromi, b) štyrmi, c) šiestimi, d) deviatimi. - Koľko je všetkých trojciferných čísel, ktoré sú vytvorené z cifier
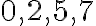 a sú deliteľné
a sú deliteľné 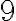 , ak sa cifry môžu opakovať?
, ak sa cifry môžu opakovať?
5. Najväčší spoločný deliteľ
Metódy:
- Výpočet pomocou množín deliteľov
- Výpočet pomocou prvočíselného rozkladu
- Výpočet pomocou najmenšieho spoločného násobku
- Výpočet pomocou Euklidovho algoritmu
Na nasledujúcom príklade si ukážeme výpočet pomocou každej metódy.
Zadanie: Nájdite najväčšieho spoločného deliteľa čísel
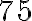 a
a 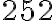 .
.
5.1. 1. Metóda - využitie množín deliteľov
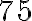 a
a 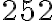 a priraďme im množiny
a priraďme im množiny 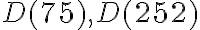 všetkých ich deliteľov. Zapíšeme tieto množiny vymenovaním prvkov aj ich prienikmi a znázorníme ich (obrázok).
všetkých ich deliteľov. Zapíšeme tieto množiny vymenovaním prvkov aj ich prienikmi a znázorníme ich (obrázok).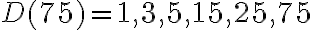
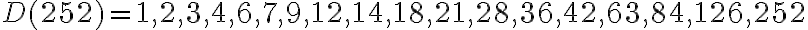
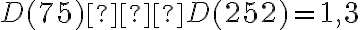
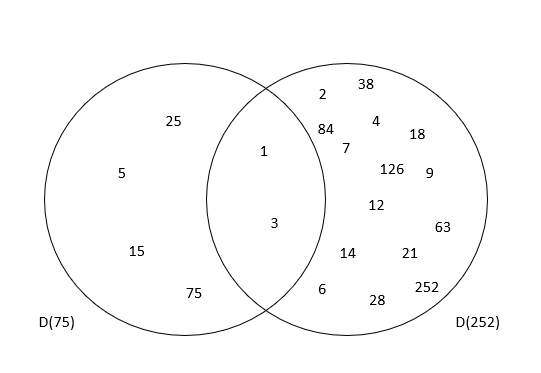
Pretože spoločné delitele čísel sú spoločné prvky množín ich deliteľov, najväčší spoločný deliteľ je najväčší prvok prieniku množín deliteľov. To platí pre dve i väčší počet čísel.
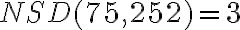
Metóda využitie množiny deliteľov sa opiera o definíciu najväčšieho spoločného deliteľa. Táto metóda je však zdĺhavá a prácna. Hodí sa len pre malé prirodzené čísla.
5.2. 2. Metóda - prvočíselný rozklad
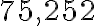 . Daným číslam priradíme ich prvočíselné rozklady (ľavý stĺpec), ktoré doplníme nultými mocninami ďalších prvočísel (pravý stĺpec). Budeme tak môcť porovnávať exponenty mocnín s rovnakými základmi.
. Daným číslam priradíme ich prvočíselné rozklady (ľavý stĺpec), ktoré doplníme nultými mocninami ďalších prvočísel (pravý stĺpec). Budeme tak môcť porovnávať exponenty mocnín s rovnakými základmi.Každý spoločný deliteľ daných čísel môže byť zapísaný mocninami tých istých prvočísel, exponent mocniny je vždy menší, alebo sa rovná tomu exponentu, ktorý je v zápisoch čísel.
Zapísali sme prvočíselné rozklady čísel
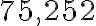 . Zostavíme z nich prvočíselný rozklad
. Zostavíme z nich prvočíselný rozklad 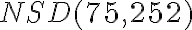 tak, že pre každé prvočíslo vyberieme najmenší exponent.
tak, že pre každé prvočíslo vyberieme najmenší exponent.5.3. 3. Metóda - pomocou najmenšieho spoločného násobku
5.4. 4. Metóda - Euklidov algoritmus
5.5. Príklady
- Obdĺžnik rozmermi
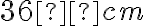 a
a 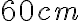 je potrebné obložiť čo najmenším počtom zhodných mozaikových štvorcov. Aká bude dĺžka strany jedného štvorca? Koľko štvorcov potrebujeme?
je potrebné obložiť čo najmenším počtom zhodných mozaikových štvorcov. Aká bude dĺžka strany jedného štvorca? Koľko štvorcov potrebujeme? - Sponzor daroval žiakom
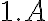 triedy
triedy 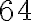 plniacich pier,
plniacich pier, 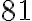 poznámkových blokov a
poznámkových blokov a 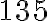 ceruziek. Žiaci si dar rozdelili tak, že každý dostal rovnaký počet pier, blokov i ceruziek. Koľko žiakov bolo v triede, keď vieme, že ich bolo viac než
ceruziek. Žiaci si dar rozdelili tak, že každý dostal rovnaký počet pier, blokov i ceruziek. Koľko žiakov bolo v triede, keď vieme, že ich bolo viac než 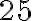 .
. - Na škole s rozšíreným vyučovaním športovej prípravy je
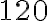 atlétov,
atlétov, 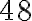 volejbalistov a
volejbalistov a 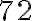 hádzanárov. Je možné rozdeliť športovcov na skupiny tak, aby počet v každej skupine bol rovnaký a vyjadrený najväčším možným číslom?
hádzanárov. Je možné rozdeliť športovcov na skupiny tak, aby počet v každej skupine bol rovnaký a vyjadrený najväčším možným číslom? - Najväčší spoločný deliteľ čísel
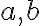 je
je 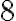 . Najmenší spoločný násobok čísel
. Najmenší spoločný násobok čísel 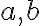 je
je 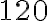 . Pritom ani
. Pritom ani 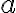 , ani
, ani 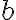 nie sú deliteľom jeden druhého. Ktoré sú to čísla?
nie sú deliteľom jeden druhého. Ktoré sú to čísla?