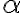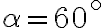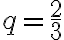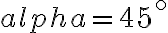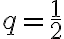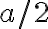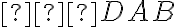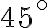Voľné rovnobežné premietanie
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Voľné rovnobežné premietanie |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | utorok, 23 apríla 2024, 17:53 |
Voľné rovnobežné premietanie
Medzi dôležité tematické oblasti stereometrie zaraďujeme aj princípy zobrazovania útvarov (telies) do roviny (priemetne). Pripomeňme si, že základný trojrozmerný geometrický útvar je jednoznačne určený svojimi význačnými bodmi1).
Obrazom geometrického útvaru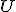 vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar
vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar 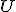 určený.
určený.
Obrazom geometrického útvaru
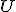 vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar
vo voľnom rovnobežnom premietaní bude geometrický útvar, ktorý pozostáva z rovnobežných priemetov všetkých význačných bodov,
ktorými je útvar 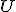 určený.
určený.
Nech 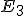 je trojrozmerný euklidovský priestor a nech rovina
je trojrozmerný euklidovský priestor a nech rovina 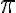 je jeho podmnožinou. Ďalej nech je daná pevná priamka
je jeho podmnožinou. Ďalej nech je daná pevná priamka 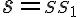 , ktorá je rôznobežná s rovinou
, ktorá je rôznobežná s rovinou  .
.
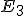 je trojrozmerný euklidovský priestor a nech rovina
je trojrozmerný euklidovský priestor a nech rovina 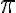 je jeho podmnožinou. Ďalej nech je daná pevná priamka
je jeho podmnožinou. Ďalej nech je daná pevná priamka 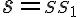 , ktorá je rôznobežná s rovinou
, ktorá je rôznobežná s rovinou  .
.
Definícia
- voľné rovnobežné premietanie2) (VRP)
Zobrazenie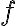 množiny všetkých bodov priestoru
množiny všetkých bodov priestoru 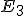 , ktoré každému bodu
, ktoré každému bodu  priradí priesečník
priradí priesečník 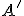 priamky
priamky 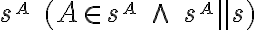 s rovinou
s rovinou  , nazveme voľné rovnobežné premietanie do roviny
, nazveme voľné rovnobežné premietanie do roviny  so smerom
so smerom 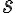 (označujeme
(označujeme 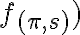 .
.
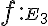
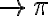 ;
; 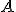
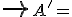
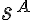
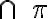 , pričom
, pričom 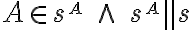
Zobrazenie
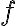 množiny všetkých bodov priestoru
množiny všetkých bodov priestoru 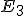 , ktoré každému bodu
, ktoré každému bodu  priradí priesečník
priradí priesečník 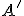 priamky
priamky 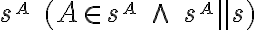 s rovinou
s rovinou  , nazveme voľné rovnobežné premietanie do roviny
, nazveme voľné rovnobežné premietanie do roviny  so smerom
so smerom 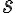 (označujeme
(označujeme 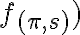 .
.
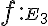
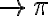 ;
; 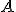
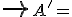
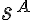
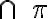 , pričom
, pričom 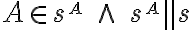
Definície
- Priamku
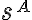 nazývame premietajúca priamka bodu
nazývame premietajúca priamka bodu  alebo smer premietania, rovinu
alebo smer premietania, rovinu  priemetňa.
Bod
priemetňa.
Bod 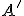
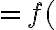
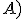 sa nazýva rovnobežný priemet bodu
sa nazýva rovnobežný priemet bodu  v danom rovnobežnom premietaní
v danom rovnobežnom premietaní 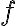 .
. - Rovnobežným priemetom
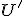 ľubovoľného geometrického útvaru
ľubovoľného geometrického útvaru 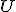 sa bude nazývať množina rovnobežných priemetov všetkých bodov útvaru
sa bude nazývať množina rovnobežných priemetov všetkých bodov útvaru 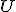 .
. - Nech
 je ľubovoľná priamka, ktorá je s priemetňou
je ľubovoľná priamka, ktorá je s priemetňou  rôznobežná. Jej priesečník s priemetňou budeme nazývať stopník priamky
rôznobežná. Jej priesečník s priemetňou budeme nazývať stopník priamky  (označenie
(označenie 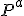 ). Analogicky priesečnicu ľubovoľnej roviny
). Analogicky priesečnicu ľubovoľnej roviny  (
(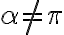 ) s priemetňou budeme nazývať stopa roviny
) s priemetňou budeme nazývať stopa roviny  (označenie
(označenie 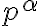 ).
).
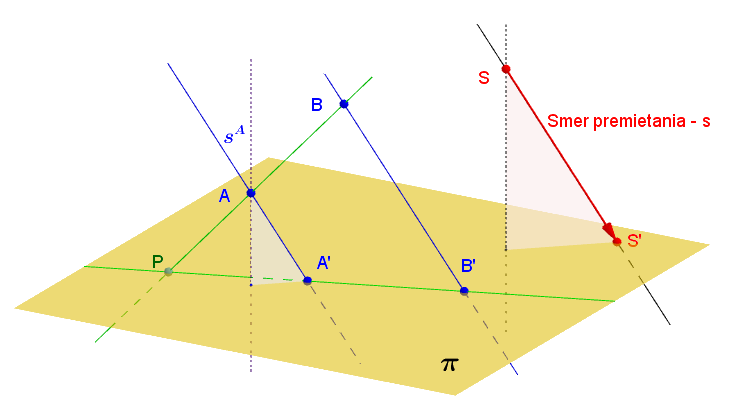
Poznámka.
V prípade, že priamka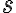 je kolmá na priemetňu s priemetňou
je kolmá na priemetňu s priemetňou  hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
V prípade, že priamka
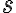 je kolmá na priemetňu s priemetňou
je kolmá na priemetňu s priemetňou  hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
hovoríme o kolmom (pravouhlom alebo ortogonálnom) premietaní. VPR - Def_Podperný trojuholník.
Cvičenie
Zostrojte obrazy troch nekolineárnych bodov vo VRP. Nájdite stopu roviny, ktorá je určená týmito troma bodmi. Zadanie si otvorte Tu.
Zostrojte obrazy troch nekolineárnych bodov vo VRP. Nájdite stopu roviny, ktorá je určená týmito troma bodmi. Zadanie si otvorte Tu.
____________________________________________________________________________________________________
1) Napríklad hranol je určený svojimi vrcholmi, valec stredmi podstáv a jedným ľubovoľným bodom kružnice určujúcej podstavu, a pod.
2) Doporučená literatúra: Hromadová, J.: Deskriptívní geometrie na MFF UK. Grant FRVŠ, UK Praha 2013. Dostupné na internete Tu.
1) Napríklad hranol je určený svojimi vrcholmi, valec stredmi podstáv a jedným ľubovoľným bodom kružnice určujúcej podstavu, a pod.
2) Doporučená literatúra: Hromadová, J.: Deskriptívní geometrie na MFF UK. Grant FRVŠ, UK Praha 2013. Dostupné na internete Tu.
...
Vlastnosti
Obrazom útvaru vo VRP je geometrický útvar, ktorý pozostáva z rovnobežných priemetov významných bodov útvaru.
Uvedieme základné vlastnosti rovnobežného premietania:
- Rovnobežným priemetom bodu je bod. Ak bod leží na priamke, tak jeho obraz bude ležať na obraze priamky.
- Rovnobežným priemetom priamky, ktorá je rovnobežná so smerom premietania, je bod.
-
Rovnobežným priemetom priamky, ktorá nie je rovnobežná so smerom premietania, je priamka.
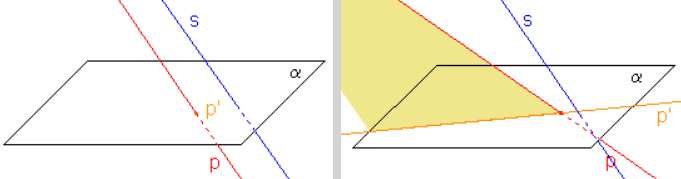
- Rovnobežným priemetom roviny, ktorá je rovnobežná so smerom premietania, je priamka.
- Rovnobežným priemetom roviny, ktorá nie je rovnobežná so smerom premietania, je celá priemetňa.
-
Rovnobežné a zhodné úsečky, ktoré nie sú rovnobežné so smerom premietania, sa zobrazia do rovnobežných a zhodných úsečiek.
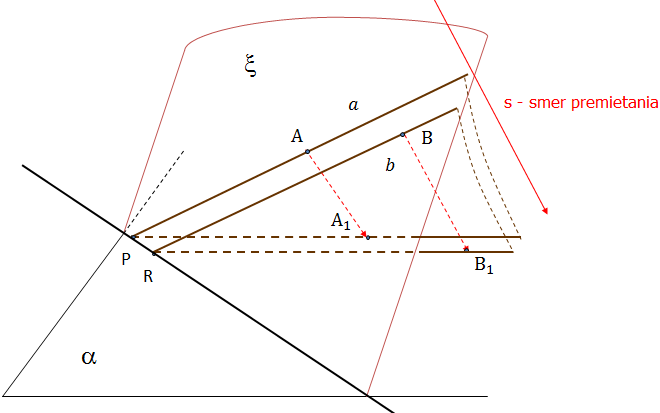
-
Stred úsečky sa v rovnobežnom premietaní zobrazí do stredu úsečky. VRP zachováva deliaci pomer.
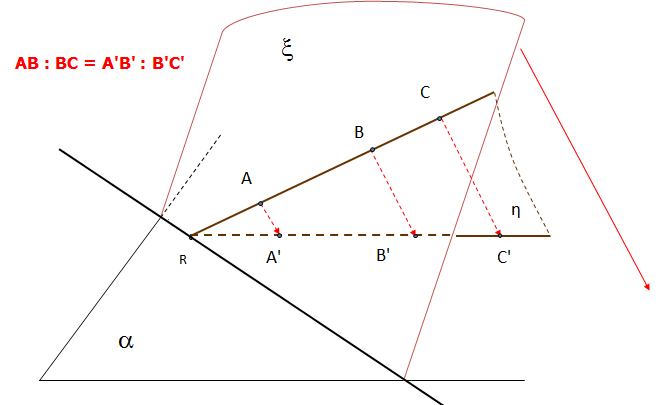
- Teleso vo VRP zobrazíme tak, že zobrazíme jeho určujúce prvky.
- Napríklad pri hranole nám stačí zobraziť jeho vrcholy, hrany resp. steny.
- Rovina rovnobežná s priemetňou sa nazýva priečelná rovina.
- Ak má teleso niektorú stenu rovnobežnú s priemetňou, tak je teleso v priečelnej polohe.
Poznámky.
V školskej praxi sa najčastejšie používa také VRP, v ktorom sa úsečka kolmá na priemetňu zobrazí do úsečky, ktorá zviera 45° uhol s obrazom úsečky rovnobežnej s priemetňou. Dĺžka zobrazenej úsečky sa zmenší na polovicu.
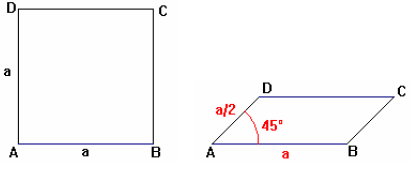
Stena telesa je rovinný geometrický útvar. Pri zobrazovaní rovinného geometrického útvaru vo VRP využívame vlastnosti uvedené v bodoch 1 až 7 a vlastnosti osovej afinity.
. V školskej praxi sa najčastejšie používa také VRP, v ktorom sa úsečka kolmá na priemetňu zobrazí do úsečky, ktorá zviera 45° uhol s obrazom úsečky rovnobežnej s priemetňou. Dĺžka zobrazenej úsečky sa zmenší na polovicu.
Stena telesa je rovinný geometrický útvar. Pri zobrazovaní rovinného geometrického útvaru vo VRP využívame vlastnosti uvedené v bodoch 1 až 7 a vlastnosti osovej afinity.
Obraz mnohouholníka
Príklad.
Vo VRP zobrazte pravidelný 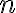 -uholník, ktorý leží v rovine kolmej na priemetňu. Strana
-uholník, ktorý leží v rovine kolmej na priemetňu. Strana 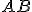 je rovnobežná s priemetňou.
je rovnobežná s priemetňou.
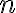 -uholník, ktorý leží v rovine kolmej na priemetňu. Strana
-uholník, ktorý leží v rovine kolmej na priemetňu. Strana 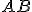 je rovnobežná s priemetňou.
je rovnobežná s priemetňou.
Poznámky
Práca so softvérom GeoGebra 3D je pomerne náročná pre žiakov na ZŠ ale aj SŠ. Učiteľ matematiky musí ovládať prácu aj v rovinnom modeli (GeoGebra 2d - Nákresňa).
V nákresni zadáme len smer premietania pomocou "Podperného trojuholníka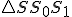 " [zadáme uhol
" [zadáme uhol 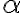 =
=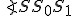 a zadáme koeficient skrátenia
a zadáme koeficient skrátenia
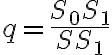 ]. Pozrite si applet Podperný trojuholník Tu.
]. Pozrite si applet Podperný trojuholník Tu.
Práca so softvérom GeoGebra 3D je pomerne náročná pre žiakov na ZŠ ale aj SŠ. Učiteľ matematiky musí ovládať prácu aj v rovinnom modeli (GeoGebra 2d - Nákresňa).
V nákresni zadáme len smer premietania pomocou "Podperného trojuholníka
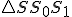 " [zadáme uhol
" [zadáme uhol 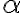 =
=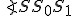 a zadáme koeficient skrátenia
a zadáme koeficient skrátenia
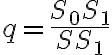 ]. Pozrite si applet Podperný trojuholník Tu.
]. Pozrite si applet Podperný trojuholník Tu.
Poznámky
Cvičenie 1.
Zostrojte obraz štvorca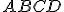 , ktorý leží vo vodorovnej rovine vzhľadom na priemetňu (rovina kolmá na priemetňu). Zadanie Tu.
Riešenie
Tu.
, ktorý leží vo vodorovnej rovine vzhľadom na priemetňu (rovina kolmá na priemetňu). Zadanie Tu.
Riešenie
Tu.
Zostrojte obraz štvorca
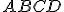 , ktorý leží vo vodorovnej rovine vzhľadom na priemetňu (rovina kolmá na priemetňu). Zadanie Tu.
Riešenie
Tu.
, ktorý leží vo vodorovnej rovine vzhľadom na priemetňu (rovina kolmá na priemetňu). Zadanie Tu.
Riešenie
Tu.
Cvičenie 2.
Zostrojte obraz kružnice vpísanej do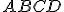 , ktorý leží v rovine kolmej na priemetňu). Zadanie
Tu.
, ktorý leží v rovine kolmej na priemetňu). Zadanie
Tu.
Zostrojte obraz kružnice vpísanej do
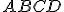 , ktorý leží v rovine kolmej na priemetňu). Zadanie
Tu.
, ktorý leží v rovine kolmej na priemetňu). Zadanie
Tu. Telesá vo VRP
Pri zobrazovaní telesa vo VRP budeme predpokladať, že teleso je umiestnené v priestore tak, aby niektorá jeho časť (stena, hrana, ...) bola v priečelnej rovine (rovina rovnobežná s priemetňou).
Úloha.
Daná je kocka (a=9cm) vo VRP(135°,5/6). Zostrojte teleso, ktoré vznikne z danej kocky, ak odrežeme časti kocky pri všetkých vrcholoch rovinami (vrchol, stredy incidentných hrán). Riešenie Tu.
Interaktívny kváder vo VRP
Tu.
Daná je kocka (a=9cm) vo VRP(135°,5/6). Zostrojte teleso, ktoré vznikne z danej kocky, ak odrežeme časti kocky pri všetkých vrcholoch rovinami (vrchol, stredy incidentných hrán). Riešenie Tu.
Prémiové úlohy - každá za 2 plusové body.
Príklady telies
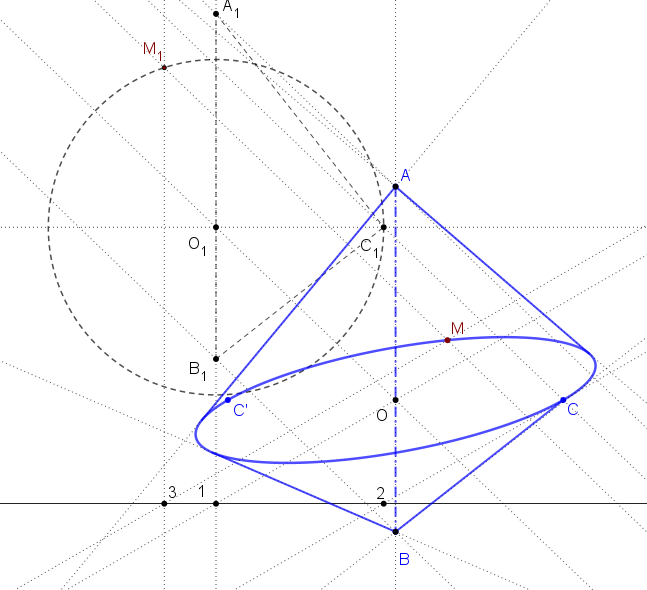
Rotačné teleso.
- VRP(
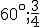 )
)
Narysujte obraz telesa, ktoré vznikne rotáciou pravouhlého trojuholníka so stranami 5,5 a 7 okolo jeho prepony. Teleso zobrazte, keď jeho os je vertikálna. Zadanie Tu. Ukážka 3D Tu. - VRP(
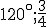 )
)
Narysujte obraz rotačného kužeľa so stredom podstavy priemerom
priemerom 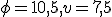 a kvádra
a kvádra 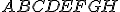 s kosoštvorcovou
podstavou
s kosoštvorcovou
podstavou 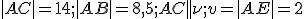 , pričom stred podstavy
, pričom stred podstavy 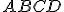 je totožný so stredom kužeľa. Zadanie Tu.
je totožný so stredom kužeľa. Zadanie Tu.
Výrez v telese.
VRP(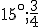 )
)
Narysujte obraz kvádra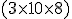 - hrana o veľkosti
- hrana o veľkosti 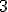 je rovnobežná s
je rovnobežná s 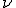 ,
hrana o veľkosti
,
hrana o veľkosti 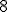 je výška, v ktorom je v bočných stenách vyrezaný kruh s priemerom
je výška, v ktorom je v bočných stenách vyrezaný kruh s priemerom 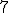 ) stred steny je totožný so
stredom kruhu).
) stred steny je totožný so
stredom kruhu).
VRP(
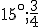 )
)
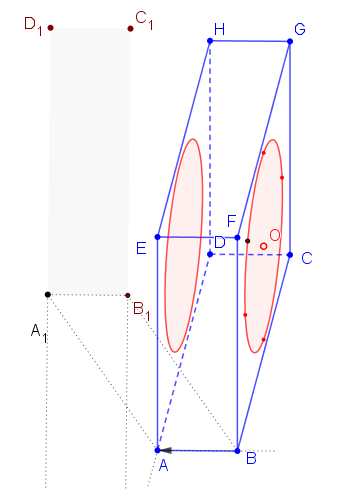
Narysujte obraz kvádra
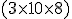 - hrana o veľkosti
- hrana o veľkosti 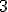 je rovnobežná s
je rovnobežná s 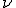 ,
hrana o veľkosti
,
hrana o veľkosti 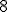 je výška, v ktorom je v bočných stenách vyrezaný kruh s priemerom
je výška, v ktorom je v bočných stenách vyrezaný kruh s priemerom 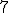 ) stred steny je totožný so
stredom kruhu).
) stred steny je totožný so
stredom kruhu).
Riešenie
Stredy stien.
VRP(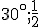 )
)
Narysujte obraz telesa, ktorého vrcholy sú stredy všetkých stien pravidelného 6-bokého hranola (polomer opísanej kružnice podstavy je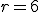 ,
výška hranola
,
výška hranola 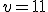 , poloha
, poloha 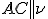 . Koľko stien má vzniknuté teleso?
. Koľko stien má vzniknuté teleso?
VRP(
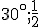 )
)
Narysujte obraz telesa, ktorého vrcholy sú stredy všetkých stien pravidelného 6-bokého hranola (polomer opísanej kružnice podstavy je
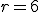 ,
výška hranola
,
výška hranola 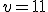 , poloha
, poloha 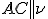 . Koľko stien má vzniknuté teleso?
. Koľko stien má vzniknuté teleso?
Riešenie
Seminárne zadania
Vo VRP riešte nasledujúce úlohy
- Zobrazte pravidelný päťuholník
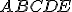 , ktorý leží vo vodorovnej rovine vzhľadom na priemetňu (rovina kolmá na priemetňu). Strana
, ktorý leží vo vodorovnej rovine vzhľadom na priemetňu (rovina kolmá na priemetňu). Strana 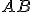 je rovnobežná s priemetňou. Zadanie
Tu
je rovnobežná s priemetňou. Zadanie
Tu - Vo VRP
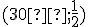 zostrojte teleso, ktorého vrcholy sú stredy stien pravidelného 4-bokého hranola,
kde
zostrojte teleso, ktorého vrcholy sú stredy stien pravidelného 4-bokého hranola,
kde 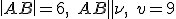 . Koľko stien má vzniknuté teleso. Zadanie
Tu
. .
. Koľko stien má vzniknuté teleso. Zadanie
Tu
. . - Vo VRP
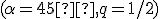 zobrazte pravidelný šesťboký hranol
zobrazte pravidelný šesťboký hranol 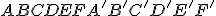 ak
ak
- Nájdite obraz kružnice
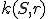 , ktorá leží v rovine kolmej na priemetňu. Dané sú súradnice bodov
, ktorá leží v rovine kolmej na priemetňu. Dané sú súradnice bodov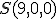 a
a 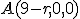 . Zadanie
Tu. Riešenie Tu. Kružnica - Rytzova konštrukcia Tu.
. Zadanie
Tu. Riešenie Tu. Kružnica - Rytzova konštrukcia Tu. - Vo VRP
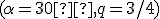 zobrazte pravidelný šesťboký hranol
zobrazte pravidelný šesťboký hranol 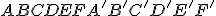 [
[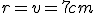 strana
strana 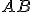 je rovnobežná s priemetňou], ktorý má v stene
je rovnobežná s priemetňou], ktorý má v stene 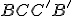 a hornej podstave narysovanú kružnicu o priemere
a hornej podstave narysovanú kružnicu o priemere 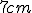 (stred steny a stred kružnice sú totožné).
(stred steny a stred kružnice sú totožné). - V pravom nadhľade
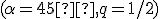 zostrojte pravidelný päťboký ihlan
zostrojte pravidelný päťboký ihlan 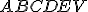 , ktorého podstava je vpísaná do kružnice o
polomere
, ktorého podstava je vpísaná do kružnice o
polomere 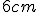 a výška má veľkosť
a výška má veľkosť 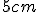 . V GeoGebre vytvorte applet podľa postupu konštrukcie na Matematická sekce,
MFF Univerzita Karlova
→
. V GeoGebre vytvorte applet podľa postupu konštrukcie na Matematická sekce,
MFF Univerzita Karlova
→
- Narysujte obraz kvádra
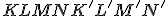 vo VRP
vo VRP 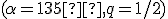 . Dané veľkosti strán
. Dané veľkosti strán 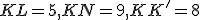 (použite posuvníky) a strana
(použite posuvníky) a strana 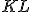 je rovnobežná s priemetňou.
je rovnobežná s priemetňou.
Ďalej sú dané body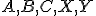 , pre ktoré platia deliace pomery
, pre ktoré platia deliace pomery
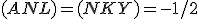 ,
,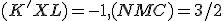 a bod
a bod 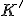 , ktorý leží medzi bodmi
, ktorý leží medzi bodmi 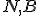 . Tiež je daná veľkosť
. Tiež je daná veľkosť 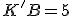 .
Určte priesečník priamky
.
Určte priesečník priamky 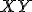 s rovinou
s rovinou 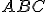 .
.
Osová afinita - riešte úlohy
- Zostrojte obraz štvorca
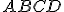 v OA:
v OA: 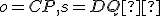 ,kde
,kde  . Zadanie Tu. Riešenie .
. Zadanie Tu. Riešenie . - Du. Zobrazte obraz štvorca
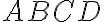 v OA: os
v OA: os
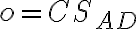 , smer
, smer
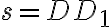 , kde
, kde
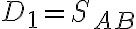 .
Použite zadanie →
.
Použite zadanie →
- style="line-height: 180%; text-align: justify">Daná je os afinity
 a kosoštvorec
a kosoštvorec
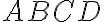 , ktorý leží v jednej polrovine určenej osou
, ktorý leží v jednej polrovine určenej osou
 . Zostrojte smer afinity tak, aby kosoštvorcu
. Zostrojte smer afinity tak, aby kosoštvorcu
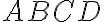 v afinite odpovedal štvorec
v afinite odpovedal štvorec
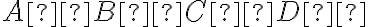 .
(500RUG, str. 147). .
Zadanie Tu. Riešenie
Tu.
.
(500RUG, str. 147). .
Zadanie Tu. Riešenie
Tu.
- Daná je os afinity
 a trojuholník
a trojuholník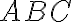 . Zostrojte pravouhlý rovnoramenný trojuholník
. Zostrojte pravouhlý rovnoramenný trojuholník 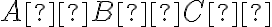 s
pravým uhlom pri vrchole
s
pravým uhlom pri vrchole
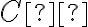 , ktorý je afinným obrazom trojuholníka
, ktorý je afinným obrazom trojuholníka
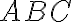 .
(500RUG, str. 149)
.
(500RUG, str. 149) - DU. Je daný rovnobežník
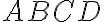 a os afinity
a os afinity
 . Dourčite osovú afinitu (určte polohu bodu
. Dourčite osovú afinitu (určte polohu bodu 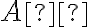 ) tak, aby obrazom rovnobežníka
bol
) tak, aby obrazom rovnobežníka
bol
- V rovine je daná osová afinita osou afinity
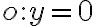 a párom odpovedajúcich bodov:
a párom odpovedajúcich bodov:
![S[0,4], S_1[−3,−5] S[0,4], S_1[−3,−5]](https://lms.umb.sk/filter/tex/pix.php/9ec85ae1a85499d729d901fd4ac4931d.png) . Nájdite hlavné a vedľajšie vrcholy elipsy, do ktorej sa zobrazí kružnica
. Nájdite hlavné a vedľajšie vrcholy elipsy, do ktorej sa zobrazí kružnica
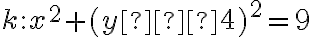 . Narysujte takúto elipsu.
→
. Narysujte takúto elipsu.
→
-
Zostrojte rez kocky rovinou
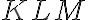 . Zadanie Tu.
. Zadanie Tu.