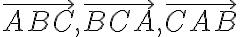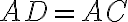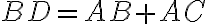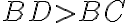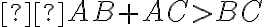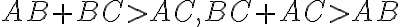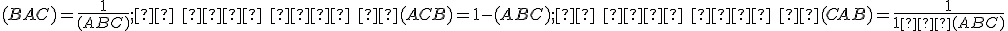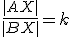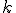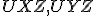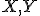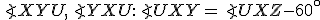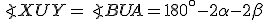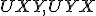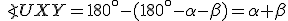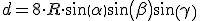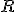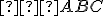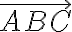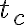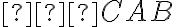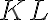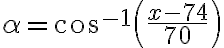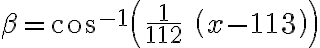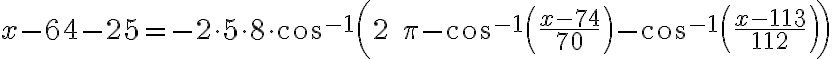Trojuholník - cvičenia
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Trojuholník - cvičenia |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | štvrtok, 25 apríla 2024, 22:27 |
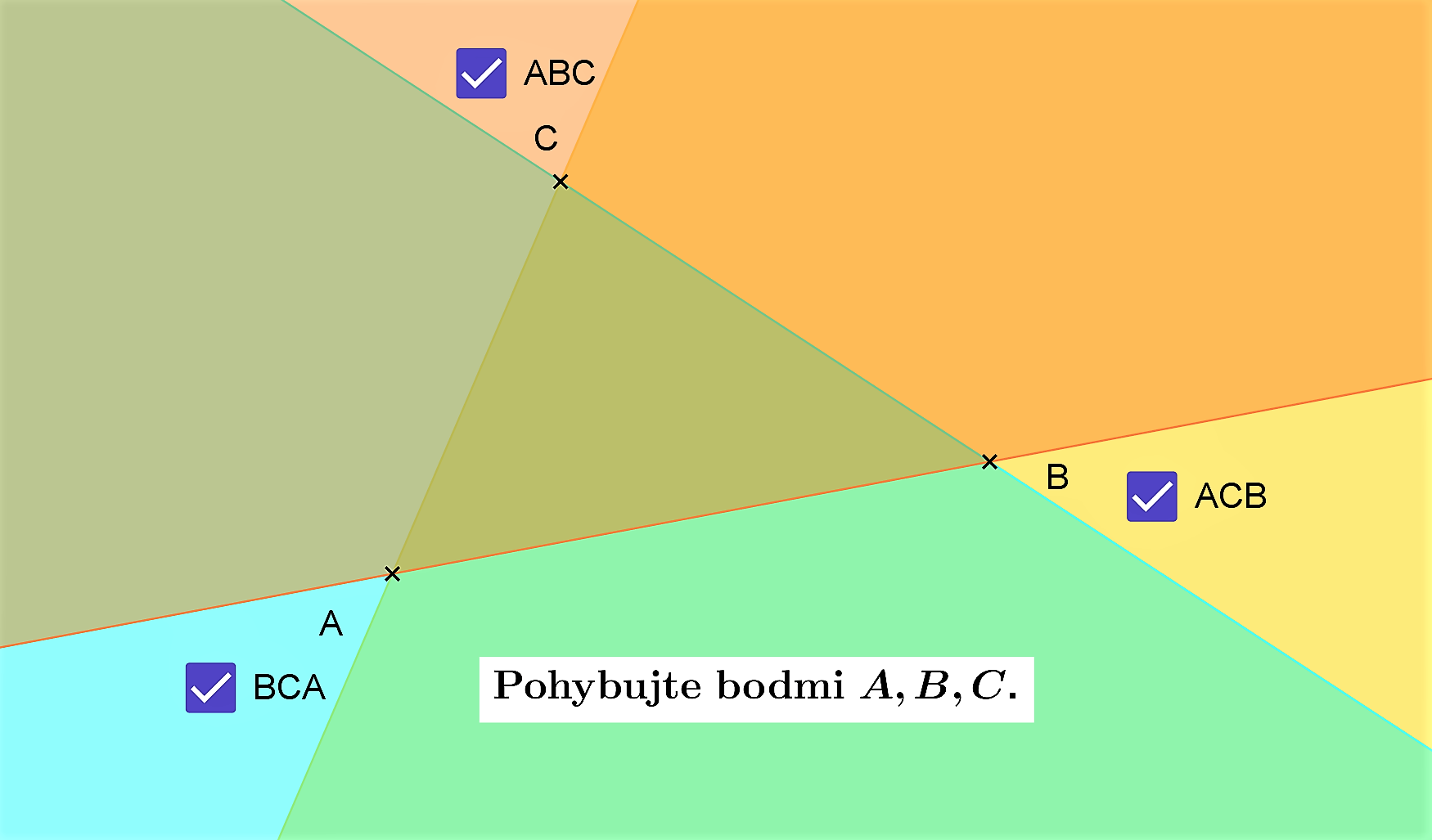
Trojuholník ABC
Definícia A (trojuholník v Hibertovom axiomatickom systéme)
Nech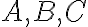 sú dané nekolineárne body. Pod trojuholníkom
sú dané nekolineárne body. Pod trojuholníkom
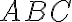 rozumieme prienik polrovín
rozumieme prienik polrovín
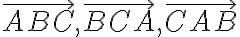 .
.
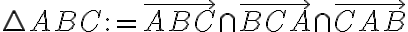
Nech
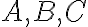 sú dané nekolineárne body. Pod trojuholníkom
sú dané nekolineárne body. Pod trojuholníkom
 rozumieme prienik polrovín
rozumieme prienik polrovín
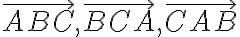 .
.
Základné pojmy
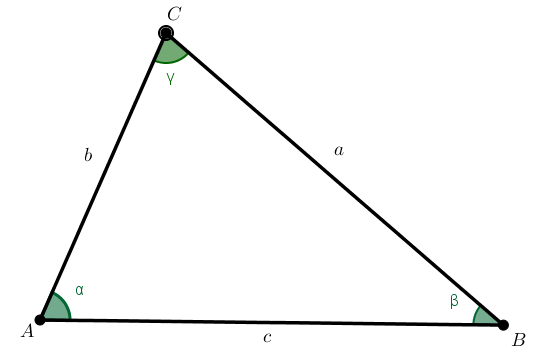
Otvorte so applet Tu
- Body
 sú jeho vrcholy.
sú jeho vrcholy. - Jednotlivé úsečky
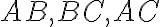 sú strany
sú strany
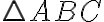 .
. - Vrcholy a strany tvoria spolu hranicu trojuholníka
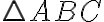 .
. - Body, ktoré sú zároveň vnútornými bodmi polrovín
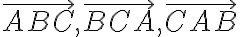 sú vnútorné body alebo
vnútro
sú vnútorné body alebo
vnútro
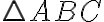 .
. - Body, ktoré neležia ani na hranici ani vnútri
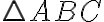 , sú vonkajšie body alebo vonkajšok
, sú vonkajšie body alebo vonkajšok
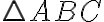 .
.

Otvorte so applet Tu
Poznámky
Dve vety o trojuholníku
Za základné vety (vlastnosti) trojuholníka považujeme nasledujúce dve vety:
- vetu o súčte vnútorných uhlov v trojuholníku
- trojuholníkovú nerovnosť
Tieto vety sa opierajú o tvrdenia súvisiace s uhlami pri základni rovnoramenného trojuholníka (Euklides Základy T/V), tvrdením o vonkajšom uhle trojuholníka(Základy T/XIII), tvrdením, že oproti väčšiemu uhlu trojuholníka leží väčšia strana (Základy T/XIX) a tvrdením T/XXIX.
Veta (Súčet vnútorných uhlov)
Súčet veľkostí všetkých vnútorných uhlov v trojuholníku je rovný 180°.
Súčet veľkostí všetkých vnútorných uhlov v trojuholníku je rovný 180°.
Poznámka.
Euklides pri dôkaze tohto tvrdenia využíva tvrdenia
Euklides pri dôkaze tohto tvrdenia využíva tvrdenia
- T/XXIX - "Priamka pretínajúca rovnobežky vytvára striedavé zhodné uhly a vonkajší uhol sa rovná opačnému vnútornému uhlu a súčet vnútorných uhlov na tej istej strane sa rovná dvom pravým uhlom."
- T/XXXI - "Daným bodom je možné zostrojiť priamku rovnobežnú s danou priamkou"
Interpretácia tvrdenia.
Presuňte vrcholy tak, aby sa všetky vrcholy prekrývali. V nasledujúcom applete aktivujte posuvník.
Euklidov dôkaz
applet
Presuňte vrcholy tak, aby sa všetky vrcholy prekrývali. V nasledujúcom applete aktivujte posuvník.
Euklidov dôkaz
applet
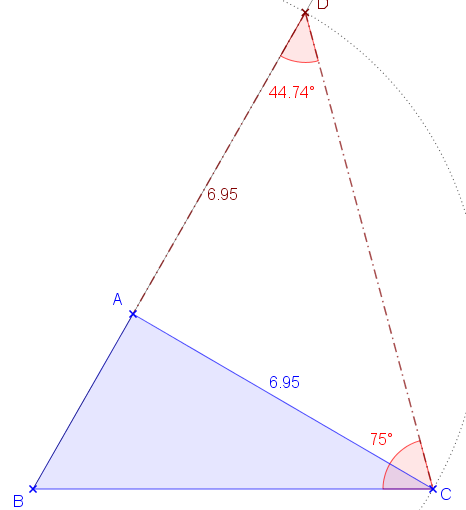
Tvrdenie (Trojuholníková nerovnosť, Euklidove Základy: Kniha prvá, Tvrdenie XX)
V každom trojuholníku ktorékoľvek dve strany (súčtom) sú dlhšie než ostávajúca tretia strana.
V každom trojuholníku ktorékoľvek dve strany (súčtom) sú dlhšie než ostávajúca tretia strana.
Dôkaz:
Nech je daný trojuholník . Na predĺžení strany
. Na predĺžení strany
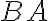 za bodom
za bodom
 zvoľme bod
zvoľme bod
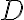 tak, aby
tak, aby
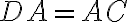 (Post. 2.)
(Post. 2.)
Trojuholník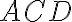 je rovnoramenný, odkiaľ dostávame:
je rovnoramenný, odkiaľ dostávame:
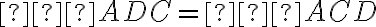 (Tvrdenie V)
(Tvrdenie V)
Teda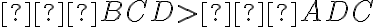 . Keďže v trojuholníku
. Keďže v trojuholníku
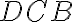 oproti väčšiemu uhlu leží dlhšia strana, platí
oproti väčšiemu uhlu leží dlhšia strana, platí
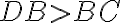 (Tvrdenie XIX)
(Tvrdenie XIX)
 Tu otvoriť →
Tu otvoriť →
Zhrňme naše výsledky: Konštrukčný dôkaz - GeoGebra →
Nech je daný trojuholník
 . Na predĺžení strany
. Na predĺžení strany
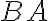 za bodom
za bodom
 zvoľme bod
zvoľme bod
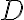 tak, aby
tak, aby
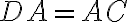 (Post. 2.)
(Post. 2.)
Trojuholník
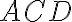 je rovnoramenný, odkiaľ dostávame:
je rovnoramenný, odkiaľ dostávame:
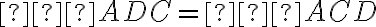 (Tvrdenie V)
(Tvrdenie V)
Teda
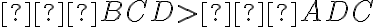 . Keďže v trojuholníku
. Keďže v trojuholníku
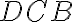 oproti väčšiemu uhlu leží dlhšia strana, platí
oproti väčšiemu uhlu leží dlhšia strana, platí
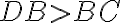 (Tvrdenie XIX)
(Tvrdenie XIX)
Zhrňme naše výsledky: Konštrukčný dôkaz - GeoGebra →
Druhy trojuholníkov
Trojuholníky môžeme rozčleniť podľa viacerých kritérií, napríklad podľa:
- dĺžky jeho strán
- veľkosti najväčšieho vnútorného uhla.
Vzhľadom na dĺžky (veľkosti) strán v danom trojuholníku rozdeľujeme trojuholníky do troch skupín
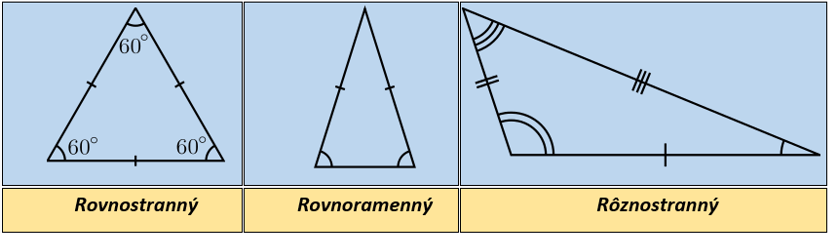
- Rovnostranný trojuholník - všetky strany trojuholníka majú rovnakú dĺžku (sú navzájom zhodné).
- Rovnoramenný trojuholník - práve (len) dve strany rovnakej dĺžky (sú navzájom zhodné).
- Rôznostranný trojuholník - všetky strany majú rozličnú dĺžku (žiadne dve strany trojuholníka nie sú zhodné).
Poznámka.
Zdôvodnenie, že neexistuje viac druhov trojuholníkov vyplýva z dichotomického hľadiska. Pre tri veľkosti strán (resp. pre tri čísla: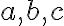 ) môžu nastať len prípady:
) môžu nastať len prípady:
1.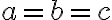 , 2.
, 2.
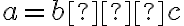 , 3.
, 3.
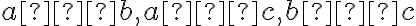
Zdôvodnenie, že neexistuje viac druhov trojuholníkov vyplýva z dichotomického hľadiska. Pre tri veľkosti strán (resp. pre tri čísla:
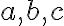 ) môžu nastať len prípady:
) môžu nastať len prípady:
1.
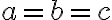 , 2.
, 2.
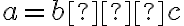 , 3.
, 3.
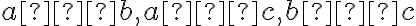
Vzhľadom na veľkosti veľkosti najväčšieho vnútorného uhla rozdeľujeme trojuholníky do troch skupín
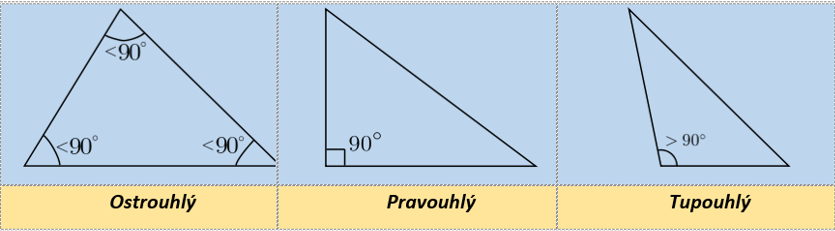
- Ostrouhlý trojuholník – má všetky vnútorné uhly menšie ako 90° (tri ostré uhly).
- Pravouhlý trojuholník – má práve jeden vnútorný uhol s veľkosťou 90° (jeden pravý uhol).
- Tupouhlý trojuholník – má práve jeden vnútorný uhol väčší ako 90° (tupý uhol) a ostatné uhly má ostré.
Ukážka.
V nasledujúcom applete pohybujte vrcholmi trojuholníka. Vytvorte rôzne typy trojuholníkov, ktoré charakterizujú veľkostí strán a veľkosti uhlov. Nájdite napríklad takú polohu vrchol trojuholníka, aby bol pravouhlý a súčasne rovnoramenný (ak taký existuje).
Koľko rôznych typov trojuholníkov reálne vznikne?
V nasledujúcom applete pohybujte vrcholmi trojuholníka. Vytvorte rôzne typy trojuholníkov, ktoré charakterizujú veľkostí strán a veľkosti uhlov. Nájdite napríklad takú polohu vrchol trojuholníka, aby bol pravouhlý a súčasne rovnoramenný (ak taký existuje).
Koľko rôznych typov trojuholníkov reálne vznikne?
Vybrané vety o trojuholníkoch
Definícia (Deliaci pomer)
Nech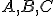 sú tri kolineárne body také, že
sú tri kolineárne body také, že 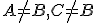 . Deliaci pomer
bodu
. Deliaci pomer
bodu  vzhľadom k bodom
vzhľadom k bodom 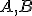 rozumieme reálne číslo
rozumieme reálne číslo 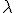 (označenie
(označenie 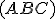 , pre ktoré platí
, pre ktoré platí
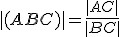 .
.
Pre bod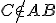 je
je 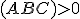 a pre bod
a pre bod 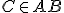 je
je 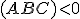 . Pre
. Pre 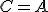 je zrejme
je zrejme 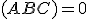 .
.
Nech
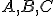 sú tri kolineárne body také, že
sú tri kolineárne body také, že 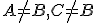 . Deliaci pomer
bodu
. Deliaci pomer
bodu  vzhľadom k bodom
vzhľadom k bodom 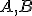 rozumieme reálne číslo
rozumieme reálne číslo 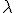 (označenie
(označenie 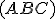 , pre ktoré platí
, pre ktoré platí
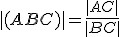 .
.
Pre bod
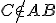 je
je 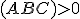 a pre bod
a pre bod 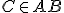 je
je 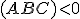 . Pre
. Pre 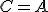 je zrejme
je zrejme 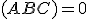 .
.
Poznámka
V niektorej literatúre sa pod deliacim pomerom troch rôznych kolineárnych bodov rozumie reálne číslo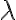 , pre ktoré platí:
, pre ktoré platí:
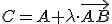 .
.
Takúto definíciu používa aj GeoGebra.
V niektorej literatúre sa pod deliacim pomerom troch rôznych kolineárnych bodov rozumie reálne číslo
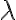 , pre ktoré platí:
, pre ktoré platí:
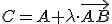 .
.
Takúto definíciu používa aj GeoGebra.
Dokážte:
Cevova veta
V trojuholníku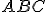 sa priamky
sa priamky 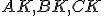 , kde
, kde 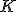 je vnútorným bodom trojuholníka
je vnútorným bodom trojuholníka 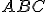 a
a 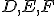 sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
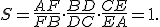
V trojuholníku
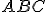 sa priamky
sa priamky 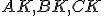 , kde
, kde 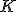 je vnútorným bodom trojuholníka
je vnútorným bodom trojuholníka 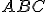 a
a 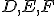 sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
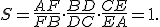
Giovanni Ceva bol taliansky matematik žijúci na prelome 17. a 18. storočia. Cevova veta stanovuje podmienku, kedy majú tri priamky prochádzajúce vrcholmi trojuholníka spoločný bod.
Dôkaz
1. (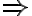 ): Ak sa priamky pretínajú v jednom bode, tak
): Ak sa priamky pretínajú v jednom bode, tak 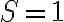 .
.
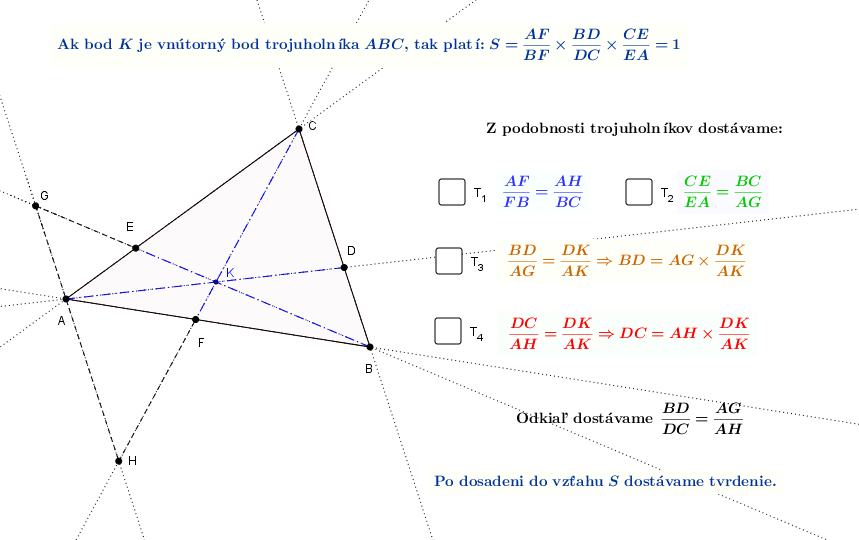
Applet otvoríte Tu
2. (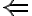 ): Ak
): Ak 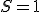 , tak sa priamky pretínajú v jednom bode.
, tak sa priamky pretínajú v jednom bode.
Pri dôkaze tejto implikácie sa vychádza z priesečníka dvoch priamok. Potom sa zostrojí priamka prechádzajúca týmto priesečníkom a tretím vrcholom. Následne sa dokáže, že táto priamka pretína protiľahlú stranu v bode, ktorý spĺňa podmienky vo vete. V dôkaze sa používajú tie isté podobnosti trojuholníkov ako v prvej časti dôkazu. Podrobnejší dôkaz nájdete v práci1).
Dôkaz
1. (
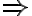 ): Ak sa priamky pretínajú v jednom bode, tak
): Ak sa priamky pretínajú v jednom bode, tak 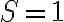 .
.

Applet otvoríte Tu
2. (
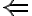 ): Ak
): Ak 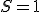 , tak sa priamky pretínajú v jednom bode.
, tak sa priamky pretínajú v jednom bode.
Pri dôkaze tejto implikácie sa vychádza z priesečníka dvoch priamok. Potom sa zostrojí priamka prechádzajúca týmto priesečníkom a tretím vrcholom. Následne sa dokáže, že táto priamka pretína protiľahlú stranu v bode, ktorý spĺňa podmienky vo vete. V dôkaze sa používajú tie isté podobnosti trojuholníkov ako v prvej časti dôkazu. Podrobnejší dôkaz nájdete v práci1).
Aplikovaním Cévovej vety dokážte, že v ľubovoľnom trojuholníku:
- Ťažnice sa pretínajú v jednom bode - ťažisku. (Využite skutočnosť, že ťažnice prechádzajú stredmi strán a každý z pomerov v Cévovej vete má tvar
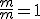 .)
.) - Výšky sa pretínajú v jednom bode - ortocentre. (Využite skutočnosť, že napr.
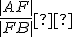
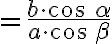 ,
ak
,
ak 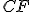 je výška.)
je výška.) - Osi vnútorných uhlov trojuholníka sa pretínajú v jednom bode - stred vpísanej kružnice. (Využite skutočnosť, že os vnútorného uhla rozdeľuje protiľahlú stranu na dve časti, ktorých dĺžky sú v rovnakom pomere ako im priľahlé strany trojuholníka.)
Neskôr tieto tvrdenia dokážeme euklidovskou metódou.
Morleyho veta.
Ak v trojuholníku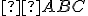 zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka
zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka 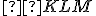 .
.
Ak v trojuholníku
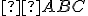 zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka
zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka 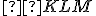 .
.
Morleyho veta predstavuje jednu z najprekvapujúcejších vlastností elementárnej geometrie, ktorú v roku 1899 objavil a dokázal anglo-americký matematik Frank Morley (1860-1937). Niektorí matematici nazývajú túto vetu aj ako Morleyov zázrak.
Dôkaz Morleyho vety nájdete vo forme appletu Tu
Poznámky k dôkazu
Dôkaz Morleyho vety nájdete vo forme appletu Tu
Poznámky k dôkazu
- V 2. kroku dôkazu zhodnosť vyplýva z vety
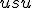 (uhly pri vrchole
(uhly pri vrchole 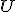 ... os uhla, pri vrchole
... os uhla, pri vrchole 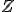 majú
veľkosť
majú
veľkosť 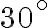 , strana
, strana 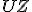 spoločná).
spoločná). - V 5. kroku dôkazu je potrebné ukázať, že trojuholník
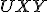 je rovnoramenný (uhly pri základni sú zhodné):
je rovnoramenný (uhly pri základni sú zhodné):
- Morleyova veta sa dá dokázať trigonometricky pomocou sínusovej a kosínusovej vety a vzorcov pre sčítanie uhlov.
_____________________________________________________________________________________________________________
1) Vallo, D.: Geometria perspektívnych trojuholníkov. FPV UKF v Nitre,2005, str.9. ISBN : 80-8050-825-9. Dostupné Tu.
1) Vallo, D.: Geometria perspektívnych trojuholníkov. FPV UKF v Nitre,2005, str.9. ISBN : 80-8050-825-9. Dostupné Tu.
Seminárne zadania
Úloha 1 Larson, Príklad 8.1.16 [1]
Modelovaním v GeoGebre nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Vyriešila Lenka Šusteková a získala plusový bod.
Vypočítajte dĺžku strany takéhoto rovnostranného trojuholníka. Plusový bod!
Modelovaním v GeoGebre nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Vyriešila Lenka Šusteková a získala plusový bod.
Vypočítajte dĺžku strany takéhoto rovnostranného trojuholníka. Plusový bod!
Úloha 2
Daný je štvorec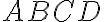 a jeho vnútorný bod
a jeho vnútorný bod 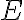 , pre ktorý platí
, pre ktorý platí
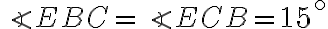 . Dokážte, že trojuholník
. Dokážte, že trojuholník
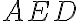 je rovnostranný.
Larson, Larson 1.6.10
je rovnostranný.
Larson, Larson 1.6.10
Daný je štvorec
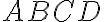 a jeho vnútorný bod
a jeho vnútorný bod 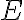 , pre ktorý platí
, pre ktorý platí
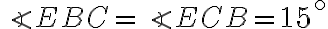 . Dokážte, že trojuholník
. Dokážte, že trojuholník
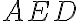 je rovnostranný.
Larson, Larson 1.6.10
je rovnostranný.
Larson, Larson 1.6.10Konštrukčná úloha
Riešenie 1. úlohy
Úloha. Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8.
Larson, Príklad 8.1.16 [1]
Riešenie 3. úlohy
Tetiva
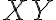 konštantnej dĺžky sa pohybuje po kružnici s priemerom
konštantnej dĺžky sa pohybuje po kružnici s priemerom
 . Stred tetivy
. Stred tetivy
 a päty kolmíc
a päty kolmíc
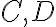 zostrojených v koncových bodov tetivy na priemer kružnice tvoria vrcholy trojuholníka. Dokážte, že trojuholník
zostrojených v koncových bodov tetivy na priemer kružnice tvoria vrcholy trojuholníka. Dokážte, že trojuholník
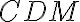 je rovnoramenný a nikdy nemení svoj tvar.
Larson, 1.2.1.
je rovnoramenný a nikdy nemení svoj tvar.
Larson, 1.2.1.
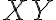 konštantnej dĺžky sa pohybuje po kružnici s priemerom
konštantnej dĺžky sa pohybuje po kružnici s priemerom
 . Stred tetivy
. Stred tetivy
 a päty kolmíc
a päty kolmíc
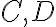 zostrojených v koncových bodov tetivy na priemer kružnice tvoria vrcholy trojuholníka. Dokážte, že trojuholník
zostrojených v koncových bodov tetivy na priemer kružnice tvoria vrcholy trojuholníka. Dokážte, že trojuholník
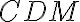 je rovnoramenný a nikdy nemení svoj tvar.
Larson, 1.2.1.
je rovnoramenný a nikdy nemení svoj tvar.
Larson, 1.2.1.
Pozri riešenie Tu