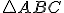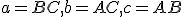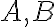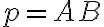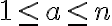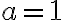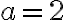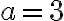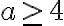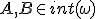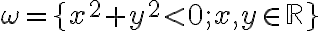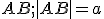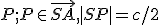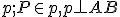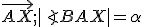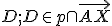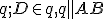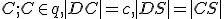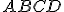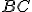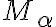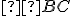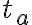Dynamický geometrický systém (DGS)
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Dynamický geometrický systém (DGS) |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 15:21 |
O programe
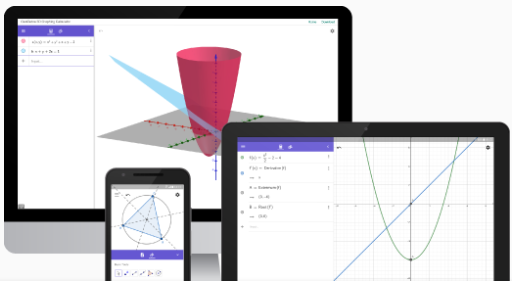
Dynamický matematický program GeoGebra, ktorý spája geometriu, algebru, analýzu, štatistiku a kalkulátor do jedného celku.
Názov GeoGebra vznikol spojením Geometria – Algebra, z čoho vyplýva aj charakter tohto softvéru.
Program je vhodný na rysovanie základných geometrických útvarov aj na algebraické výpočty. Autorom programu je Markus Hohenwarter 1).
Program je voľne šíriteľný. Stiahnite si program GeoGebra Klasik 5 zo stránky https://www.geogebra.org/download 2).
Program je vhodný na rysovanie základných geometrických útvarov aj na algebraické výpočty. Autorom programu je Markus Hohenwarter 1).
Program je voľne šíriteľný. Stiahnite si program GeoGebra Klasik 5 zo stránky https://www.geogebra.org/download 2).

Cvičenie.
Otvorte si pracovný hárok a zostrojte niektoré základné geometrické útvary: body, priamky, ...
Otvorte si pracovný hárok a zostrojte niektoré základné geometrické útvary: body, priamky, ...
1) V súčasnosti je profesorom na Univerzite v Linzi
2) Pozrite si stránku "Návody k aplikaci GeoGebra Classic" resp. Manuál
2) Pozrite si stránku "Návody k aplikaci GeoGebra Classic" resp. Manuál
Základné nástroje
Po spustení programu GeoGebra Classik 5 sa zobrazí
- v hornej časti pracovnej plochy hlavné menu a lišta s nástrojmi
- vľavo - Algebraické okno, vpravo - Nákresňa a dole - Vstup/vstupné pole resp. príkazový riadok
- východiskové nastavenie je možné upraviť pomocou menu Vzhľad
- nastavte si farbu, štýl a popis bodu, ... a potom si uložte prázdny prednastavený výkres pod názvom "PrednaskaGeoGebra_Vykres1".
Komentár k riešeniu
- Otvorte si prednastavený pracovný výkres Tu.
- Pomocou menu Vzhľad si aktivujte aj Postup konštrukcie
- v časti Nákresňa budeme rysovať
- v Geometrickom okne 2 budeme zapisovať komentár k riešeniu
- v okne Postup konštrukcie program automaticky zapisuje kroky konštrukcie.
- Riešenie zahŕňa nasledujúce kroky:
- vytvorenie posuvníkov
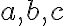
- zostrojenie bodu
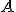 a úsečky s danou dĺžkou
a úsečky s danou dĺžkou 
- zostrojenie kružníc
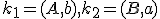 a ich priesečníka
a ich priesečníka 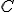
- zapisovanie komentárov.
- V prípade, že chcete zobraziť len oblúčiky pri priesečníkoch dvoch kružníc (resp. kružnice a priamky; dvoch priamok),stačí aktivovať "Vlastnosti" pre daný priesečník a začiarknuť políčko "Zobraziť upravené priesečníky priamok". Tento postup sa dá použiť aj pre priesečník dvoch priamok.
- Nastavte posuvníky
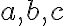 tak, aby úloha mala 2 riešenia resp. jedno alebo nemala riešenie.
tak, aby úloha mala 2 riešenia resp. jedno alebo nemala riešenie. - Konštrukciu si môžete stiahnuť Tu.
Poznámky.
- Konštrukcia uvedená pre prípad
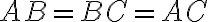 je prvým tvrdením v Euklidových Základoch (
je prvým tvrdením v Euklidových Základoch (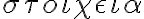 ).
). - Ide vlastne o prvý matematický dôkaz aj z pohľadu historického. Pred Euklidom existovali tvrdenia ale bez dôkazu, pozrite si napríklad tvrdenia od Tálesa Tu.
- Je prekvapujúce, že taký krátky, jasný a zrozumiteľný dôkaz môže mať logické medzery. V priebehu storočí si vyslúžil viac kritiky ako ktorýkoľvek iný dôkaz.
-
Zeno Sidon2) : "Nepreukázalo sa, že strany sa nestretnú skôr, ako dosiahnu vrcholy."
- Existujú modely geometrie, v ktorých sa kruhy nepretínajú. Napr. afinný priestor nad poľom racionálnych čísel.
- Potrebné sú ďalšie postuláty napr. :
- "Dvoma rôznymi bodmi prechádza práve jedna priamka."
- "Ak je súčet polomerov dvoch kruhov väčší ako úsečka spájajúci ich stredy, potom sa dva kruhy pretínajú."
Dynamické geometrické systémy sa vyznačujú vysokou mierou interaktivity a vizualizácie.
- Interaktivita DGS umožňuje zmenu vstupných parametrov, ktorá indukuje zmeny v skonštruovaných útvarov. Interaktívna zmena môže byť polohová alebo metrická. Príklady: Padajúci rebrík; Hypocykloida.
- Vizualizácia je schopnosť znázorniť základné aj odvodené geometrické pojmy a vzťahy medzi nimi. (Žilková, 2011)1)
- Úroveň vizualizácie priamo závisí od reprezentácie východiskových elementárnych pojmov/objektov.
- Východiskovým pojmom v DGS je bod.
- Odvodené pojmy (priamka, kruh, ...) sú definované ako množiny bodov s danou vlastnosťou v súlade s axiomatickým poňatím geometrie.
V GeoGebre je bod vizuálne modelovaný ako "krúžok" ale reálne je bod reprezentovaný ako usporiadaná dvojica reálnych čísel.
Poznámky.
- V DGS môže byť bod modelovaný aj pomocou iných symbolov, napríklad sa používajú symboly
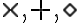 .
. - Väčší výber symbolov rôznej hrúbky a širokej farbenej škále pomáha rozvíjať geometrickú predstavivosť.
- Symbolicky pre bod platí
![A \in E_2 \Leftrightarrow A=[a,b];a,b \in R A \in E_2 \Leftrightarrow A=[a,b];a,b \in R](https://lms.umb.sk/filter/tex/pix.php/b7f7d596c35dada9d2f4fe69f48ff3bf.png) .
. - Priamka je určená práve dvoma rôznymi bodmi. V GeoGebre je priamka modelovaná pomocou grafu lineárnej funkcie.
- Úsečka ako množina bodov, ktoré ležia medzi dvoma bodmi.
___________________________________________________________________________________________________________________________________________________________________
1) Žilková, K.: DYNAMICKÉ GEOMETRICKÉ SYSTÉMY (DGS) - SOFTVÉROVÁ PODPORA VZDELÁVANIA. Journal of Technology and Information Education.
Časopis pro technickou a informační výchovu. 1/2011, Volume 3, Issue 1, ISSN 1803-537X. Dostupné na https://jtie.upol.cz/pdfs/jti/2011/01/12.pdf.
2) Epikureánsky filozof zo začiatku prvého storočia B.C.E. (nezamieňať si so Zenom z Eley, ktorý je známy paradoxmi).
1) Žilková, K.: DYNAMICKÉ GEOMETRICKÉ SYSTÉMY (DGS) - SOFTVÉROVÁ PODPORA VZDELÁVANIA. Journal of Technology and Information Education.
Časopis pro technickou a informační výchovu. 1/2011, Volume 3, Issue 1, ISSN 1803-537X. Dostupné na https://jtie.upol.cz/pdfs/jti/2011/01/12.pdf.
2) Epikureánsky filozof zo začiatku prvého storočia B.C.E. (nezamieňať si so Zenom z Eley, ktorý je známy paradoxmi).
Geometrické útvary
Nástroje programu GeoGebra na rysovanie základných geometrických útvarov
Vyskúšajte si konštrukcie rôznych druhov útvarov v prednastavenom výkrese, ktorý si stiahnite
Tu.
Program GeoGebra má na hlavnej lište rozbaľovacie ikonky/nástroje, ktoré umožňujú vykresliť základné rovinné geometrické útvary. Napríklad ikonka
- Priamka
umožňuje narysovať rôzne jednorozmerné útvary - priamku, úsečku, polpriamku, vektor ...
- Kliknite na túto ikonku v stiahnutom pracovnom hárku a prezrite si ponuku.
- Vyberte požadovaný nástroj a narysujte zvolený geometrický útvar.
- Kolmica
umožňuje narysovať kolmicu, rovnobežku, os úsečky a uhla, dotyčnice ...
- Opakujte postup: Vyberte požadovaný nástroj a narysujte zvolený geometrický útvar.
 .
.
Poznámky.
- GeoGebra umožňuje manipulovať s geometrickými útvarmi, ktoré sa zobrazujú v nákresni.
- Základným atribútom manipulácie je dynamická zmena polohy bodu, ktorá zachováva incidenciu bodu a geometrického útvaru.
- Pri používaní DGS sa objavujú slovné spojenia - premiestniť bod, pevný resp. voľný bod, zmena štýlu bodu ... Vallo, Žilková.
- Zmena polohy bodu má veľký význam, ak skúmame vlastnosť útvaru v závislosti od polohy determinujúcich bodov tohto útvaru.
- Pri klasickom spôsobe vyučovania geometrie (papier, pravítko, ceruzka) premiestniť bod nie je možné. Narysovaný bod je vždy pevný.
- Dynamická zmena polohy útvarov, pričom sa nenaruší incidencia týchto útvarov, iniciovala názov dynamické geometrické softvéry.
Definícia.
Budeme hovoriť, že bod pri transformácii
pri transformácii 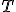 je premiestnený do bodu
je premiestnený do bodu 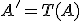 , ak platí:
, ak platí:
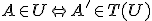 .
.
Pri premiestňovaní incidencia sa zachováva.
Budeme hovoriť, že bod
 pri transformácii
pri transformácii 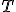 je premiestnený do bodu
je premiestnený do bodu 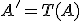 , ak platí:
, ak platí:
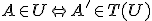 .
.
Pri premiestňovaní incidencia sa zachováva.
Príklad.
V trojuholníku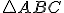 zostrojte výšky trojuholníka. Pri premiestňovaní vrcholov trojuholníka budú sa výšky pretínať v jednom bode?
zostrojte výšky trojuholníka. Pri premiestňovaní vrcholov trojuholníka budú sa výšky pretínať v jednom bode?
V trojuholníku
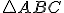 zostrojte výšky trojuholníka. Pri premiestňovaní vrcholov trojuholníka budú sa výšky pretínať v jednom bode?
zostrojte výšky trojuholníka. Pri premiestňovaní vrcholov trojuholníka budú sa výšky pretínať v jednom bode?
- Postup konštrukcie si stiahnite Tu.
- Vytvorte si vlastnú konštrukciu v novom pracovnom hárku, ktorý si stiahnite Tu.
- Riešenie zahŕňa nasledujúce kroky:
- zostrojenie bodov a zostrojenie trojuholníka
- priesečník výšok je priesečník kolmíc/priamok, ktoré sú kolmé na priamky prechádzajúce vrcholmi trojuholníka.
- Celú konštrukciu si stiahnete Tu.
Poznámka.
Pozrite si vyjadrenie Alberta Einsteina o Euklidových Základoch a o dôkaze, že výšky trojuholníka sa pretínajú v jednom bode Tu.
Pozrite si vyjadrenie Alberta Einsteina o Euklidových Základoch a o dôkaze, že výšky trojuholníka sa pretínajú v jednom bode Tu.
Začiarkavacie políčko
Zobrazenie resp. skrytie objektov
Práca s textom
GeoGebra umožňuje zobrazovať text v rôznych formátoch
- Preddefinované štýly textu: Sans Serif, Serif, Bold, Kurzíva. Farby neobmedzene.
- Napríklad aktivovaním nástroja
po vložení TeX zápisu:
\textbf \textit \textcolor{00005A} {<strong>Navy</strong>} \; \textbf \textcolor{red} {<strong>Red</strong>} \; \textit \textbf \textcolor{0BDF00} {<strong>Green</strong>}
sa zobrazí/vytvorí text
→
- Môžeme vytvoriť kombináciu normálneho textu s TeX príkazom. Napr. pre text "
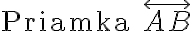 " má príkaz tvar (zápis):
" má príkaz tvar (zápis):
\text{Priamka } \overleftrightarrow{AB} - V nasledujúcej tabuľke je niekoľko ukážok textov, kliknite na príslušný odkaz.
- LaTeX zápisy, pričom je možné vkladať základné matematické výrazy a symboly. Pozrite si ponuku pre TeX →.
- Vytvoriť dynamický text - príkaz: Ak( <Podmienka1>, <Text 1>, <Podmienka 2>, <Text 2>, ..., <Inak>) vytvorí resp. zobrazí
- text "Text 1", keď je splnená prvá podmienka, "Text 2", ak je splnená druhá podmienka atď.
- ak nie je splnená žiadna z podmienok, tak zobrazí text "Inak".
Úloha1.
V nákresni narysujte dva body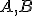 a priamku
a priamku 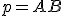 . Aktivujte Geometrické okno 2. Vytvorte TeX zápisy/texty v nákresni a zároveň aj geometrickom okne.
. Aktivujte Geometrické okno 2. Vytvorte TeX zápisy/texty v nákresni a zároveň aj geometrickom okne.
V nákresni narysujte dva body
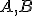 a priamku
a priamku 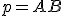 . Aktivujte Geometrické okno 2. Vytvorte TeX zápisy/texty v nákresni a zároveň aj geometrickom okne.
. Aktivujte Geometrické okno 2. Vytvorte TeX zápisy/texty v nákresni a zároveň aj geometrickom okne.- \text{Zvoľme si dva rôzne body }A\left [ x_a,y_a \right ]= objekt A ,B\left [ x_b,y_b \right ]= objekt B
- \text{Priamka }p=\overleftrightarrow{AB}
- \text{Priesečník }P∈a_x \; ∩ \; b_y; \; \;( a_x∥x, \; b_y∥y)
- \text{Orientovaný uhol } α=∡\widehat{PAB}= objekt α
- \text{Smernica }\blue k=tg \: α=\frac{y_b-y_a}{x_b-x_a}=\blue { k }
Postup konštrukcie
Program GeoGebra umožňuje zobraziť postup konštrukcie, prípadne prehrať celú konštrukciu.
- V hlavnom menu vyberte Vzhľad a potom zvoľte
- Postup konštrukcie. Zobrazí sa nové okno vpravo od nákresne, kde môžete sledovať jednotlivé konštrukčné kroky.
- Geometrické okno 2. V okne aktivujte mriežku.
- Algebraické okno. Zobrazí sa nové okno vľavo od nákresne, v ktorom sú hodnoty zostrojených útvarov.
- Tento postup interpretujeme na nasledujúcom príklade.
Príklad.
Zostrojte priamku, ktorá prechádza bodmi . V Geometrickom okne 2 zapíšte:
. V Geometrickom okne 2 zapíšte:
Zostrojte priamku, ktorá prechádza bodmi
 . V Geometrickom okne 2 zapíšte:
. V Geometrickom okne 2 zapíšte:
- text vyjadrujúci hodnotu smernice priamky
- rovnicu priamky Pre texty použite matematický TeX formát. V okne Postup konštrukcie vytvorte vhodné body lomu.
Pokúste sa o vlastnú konštrukciu v novom pracovnom hárku Tu.
Texty
Nový nástroj
Program GeoGebra má k dispozícii pomerne veľa nástrojov na narysovanie základných geometrických útvarov tak v rovine ako aj 3D priestore.
Niekedy pri konštrukciách, ktoré sú úzko tematicky zamerané, sa vyskytne potreba vytvoriť nový nástroj.
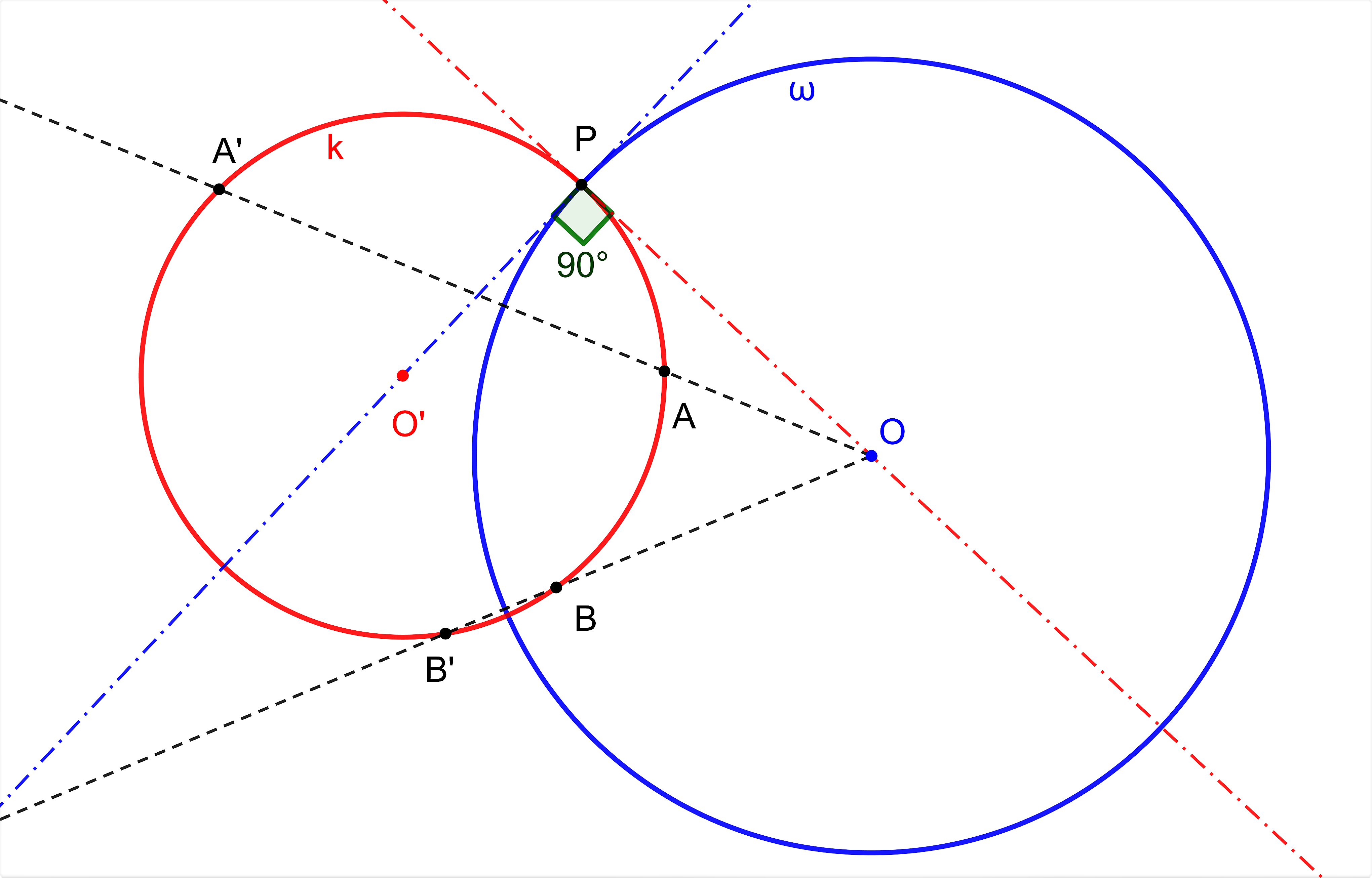
Napríklad euklidovská konštrukcia na zostrojenie dvoch navzájom kolmých kružníc je východisková konštrukcia aj pre hyperbolickú neeuklidovskú geometriu. Preto by bolo výhodné mať k dispozícii nástroj v GeoGebre, ktorý vytvorí/vykreslí takúto kružnicu.
 Otvorte si applet Tu
Otvorte si applet Tu
Napríklad euklidovská konštrukcia na zostrojenie dvoch navzájom kolmých kružníc je východisková konštrukcia aj pre hyperbolickú neeuklidovskú geometriu. Preto by bolo výhodné mať k dispozícii nástroj v GeoGebre, ktorý vytvorí/vykreslí takúto kružnicu.
 Otvorte si applet Tu
Otvorte si applet Tu
Definícia
Budeme hovoriť, že kružnice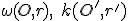 sú navzájom kolmé (ortogonálne), ak platí
sú navzájom kolmé (ortogonálne), ak platí
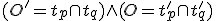
zostrojené v ich priesečníkoch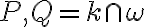 sú tiež navzájom kolmé.
sú tiež navzájom kolmé.
Budeme hovoriť, že kružnice
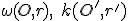 sú navzájom kolmé (ortogonálne), ak platí
sú navzájom kolmé (ortogonálne), ak platí
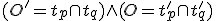
zostrojené v ich priesečníkoch
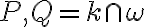 sú tiež navzájom kolmé.
sú tiež navzájom kolmé.
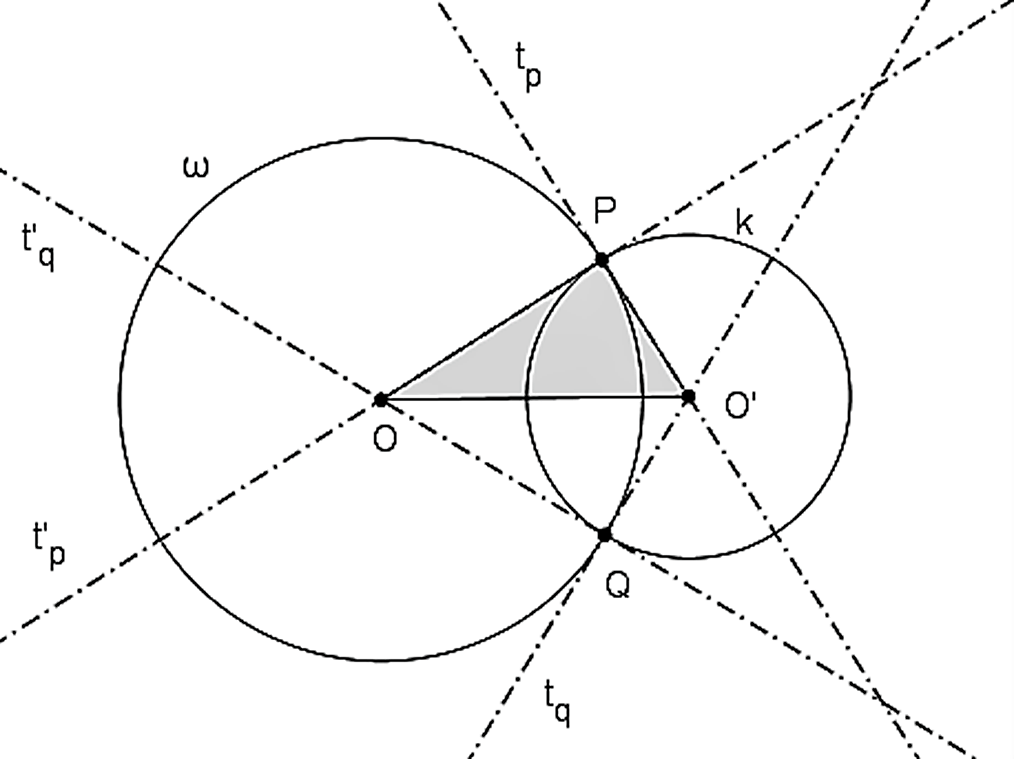
Korektnosť definície vyplýva z konštrukcie znázornenej na obrázku.
» Polomer
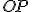 kružnice
kružnice 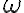 a jej dotyčnica
a jej dotyčnica 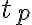 sú na seba kolmé.
sú na seba kolmé.
» Trojuholník
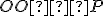 resp. trojuholník
resp. trojuholník 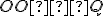 je pravouhlý.
je pravouhlý.
Rozbor úlohy
Musíme rozlíšiť tri samostatné prípady
Musíme rozlíšiť tri samostatné prípady
- Ak sú body
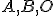 kolineárne, tak reálne neexistuje kružnica
kolineárne, tak reálne neexistuje kružnica 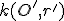 prechádzajúca cez
prechádzajúca cez 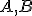 .
Stred takejto kružnice je nevlastný bod. Priamku
.
Stred takejto kružnice je nevlastný bod. Priamku 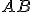 budeme považovať za jedno z riešení našej úlohy.
Má to zmysel práve pri neeuklidovskej geometrii.
budeme považovať za jedno z riešení našej úlohy.
Má to zmysel práve pri neeuklidovskej geometrii. - Body
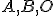 sú nekolineárne a napríklad
sú nekolineárne a napríklad 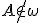 .
V tomto prípade budeme postupovať tak, že postupne zostrojíme:
.
V tomto prípade budeme postupovať tak, že postupne zostrojíme:
→ Bod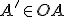 tak, aby
tak, aby 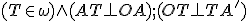 .
.
→ Kružnicu k, ktorá prechádza bodmi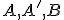 .
.
Z mocnosti bodu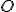 ku kružnici
ku kružnici  vyplýva, že
vyplýva, že 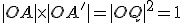 .
.
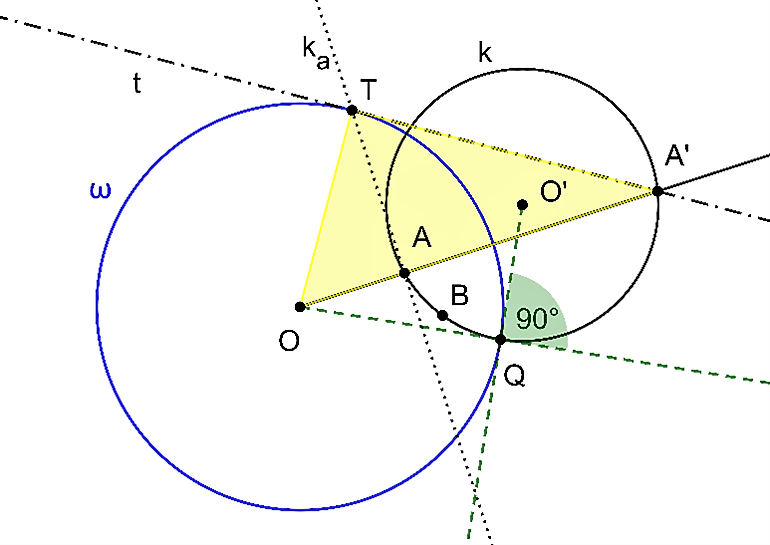
Posledná rovnosť hovorí, že kružnice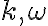 sú ortogonálne.
sú ortogonálne. - Obidva body
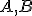 ležia na kružnici
ležia na kružnici 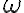 . V takom prípade stačí zostrojiť priesečník
. V takom prípade stačí zostrojiť priesečník 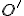 dotyčníc ku kružnici
dotyčníc ku kružnici
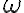 v bodoch
v bodoch 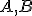 . Priesečník
. Priesečník 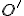 je stred hľadanej kružnice
je stred hľadanej kružnice  .
.
Riešenie
Pre každý prípad 1, 2, 3 vytvoríme samostatnú konštrukciu kružnice , ktoré si vhodne nazveme pre prípad:
, ktoré si vhodne nazveme pre prípad:
1. použijeme názov „Diameter“
2. použijeme názov „Oblúk“
3. použijeme názov „Ideál“
Po vytvorení takýchto troch samostatných konštrukcií kružníc potom vytvoríme rozhodovací blok, v ktorom na základe polohy bodov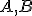 vzhľadom ku kružnici
vzhľadom ku kružnici 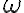 vyberieme odpovedajúcu kružnicu
vyberieme odpovedajúcu kružnicu  - Diameter, Oblúk, Ideál.
- Diameter, Oblúk, Ideál.
Pre každý prípad 1, 2, 3 vytvoríme samostatnú konštrukciu kružnice
 , ktoré si vhodne nazveme pre prípad:
, ktoré si vhodne nazveme pre prípad:
1. použijeme názov „Diameter“
2. použijeme názov „Oblúk“
3. použijeme názov „Ideál“
Po vytvorení takýchto troch samostatných konštrukcií kružníc potom vytvoríme rozhodovací blok, v ktorom na základe polohy bodov
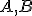 vzhľadom ku kružnici
vzhľadom ku kružnici 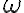 vyberieme odpovedajúcu kružnicu
vyberieme odpovedajúcu kružnicu  - Diameter, Oblúk, Ideál.
- Diameter, Oblúk, Ideál.
Diameter – príkazy v GeoGebre.
P1: Priesečník(Kružnica((0, 0), 1), Priamka(A, B), 1)
P2: Priesečník(Kružnica((0, 0), 1), Priamka(A, B), 2)
o: OsÚsečky(P1, P2)
c1: Kružnica((0, 0), 1000)
O1: Priesečník(c1, o, 1)
Diameter: Kružnica(O1, 1000)
Oblúk – príkazy v GeoGebre.
A‘: Súmernosť(A, Kružnica((0, 0), 1))
B‘: Súmernosť(B, Kružnica((0, 0), 2))
Oblúk: Ak(Dĺžka(A) ≟ 1, Kružnica(A, B, B'), Kružnica(A, B, A'))
Ideál – príkazy v GeoGebre.
p1: Kolmica(A, Priamka((0, 0), A))
p2: Kolmica(B, Priamka((0, 0), B))
O3: Priesečník(p1, p2)
Ideál: Kružnica(O3, A)
Všetky tri konštrukcie „Diameter“, „Oblúk“ a „Ideál“ spojíme do jednej konštrukcie s názvom „Kolmá Kružnica“. Výsledok vidíme na obrázku.
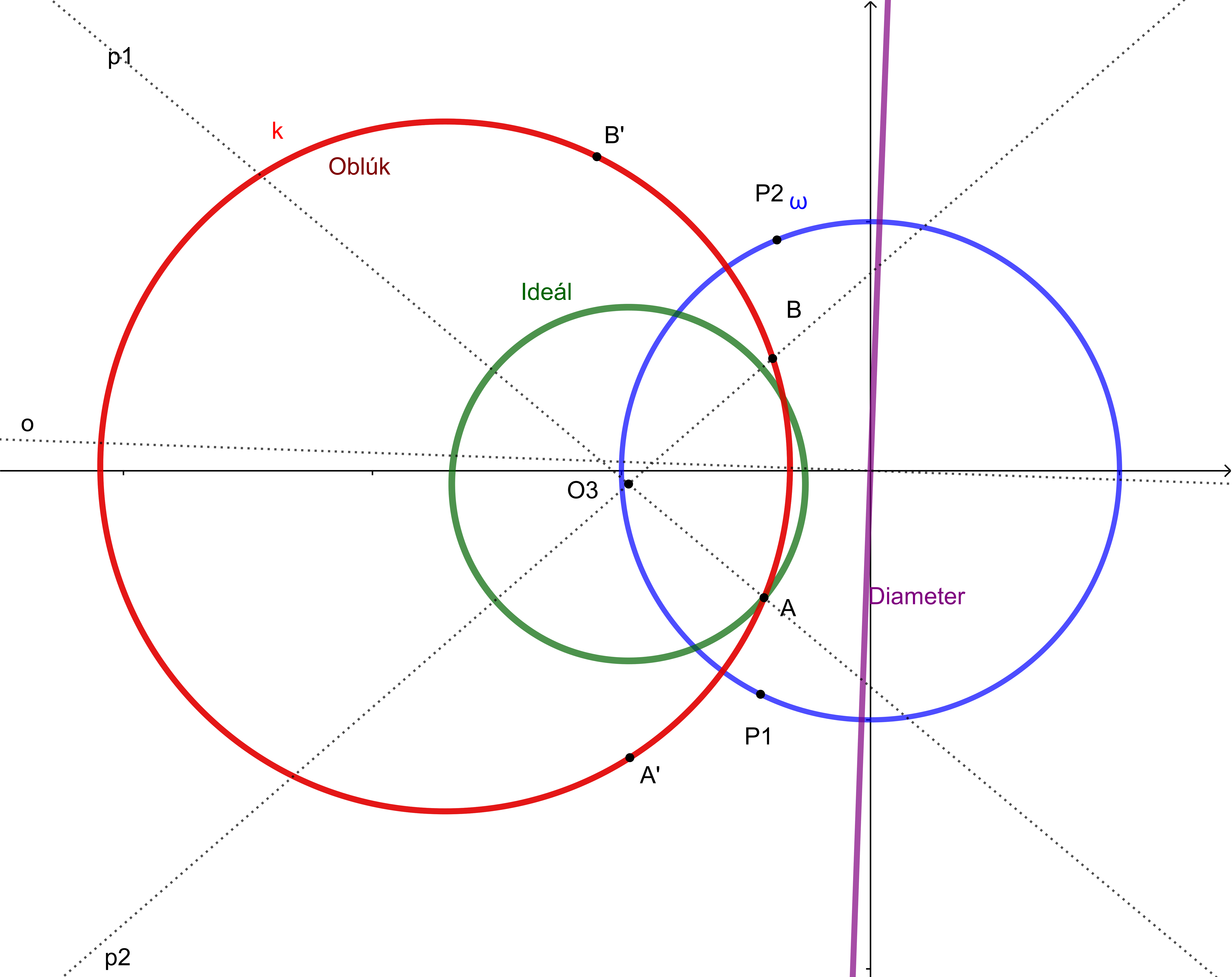
Applet si stiahnete Tu.
Postup na vytvorenie nástroja
- Spustite program GeoGebra a otvorte si súbor "Kolmá Kružnica".
- V základnom Menu programu GeoGebra vyberte možnosť "Vytvoriť nový nástroj".
- Postupujte podľa pokynov pre vytvorenie nástroja:
- ako výstupné objekty vyberte kružnicu
 (otvorte si aj algebraické okno)
(otvorte si aj algebraické okno) - ako vstupné objekty vyberte body:

- vhodne pomenujte nástroj, napr. "Kolmá kružnica", vyberte predtým vytvorený obrázok pre ikonu
- v nápovedi uveďte napr. "Ukáž dva body
- zaškrtnite políčko "Ukázať na palete nástrojov" (nie je nutné).
- ako výstupné objekty vyberte kružnicu
- Uložte si tento súbor napr. s názvom "Kolmá kružnica". Kompletnú konštrukciu si stiahnite Tu.
Poznámka
Poincare Disc
Využite Poincaré Disk vytvorený v prostredí GeoGebra, v ktorom vieme zostrojiť hyperbolickú úsečku a priamku; kružnicu určenú stredom a bodom resp. polomerom; vieme určiť vzdialenosť dvoch bodov.
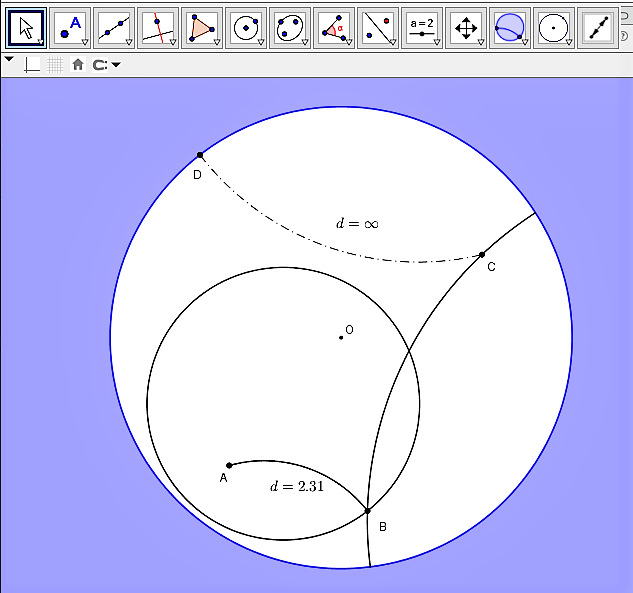
Poincaré Disk si môžete stiahnuť Tu
Poincaré Disk si môžete stiahnuť Tu
Cvičenia
- Zostrojte rovnostranný trojuholník
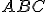 pomocou hyperbolických kružníc
pomocou hyperbolických kružníc 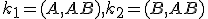 (pozrite si Euklidovo tvrdenie T/I).
(pozrite si Euklidovo tvrdenie T/I).
Riešenie Tu. - Zostrojte rovnoramenný trojuholník
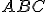 so základňou
so základňou 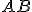 pomocou dvoch zhodných hyperbolických kružníc (kružnice s rovnakým polomerom).
Pomocou dotyčníc k hPriamkam
pomocou dvoch zhodných hyperbolických kružníc (kružnice s rovnakým polomerom).
Pomocou dotyčníc k hPriamkam 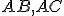 a k hPriamkam
a k hPriamkam 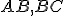 určte veľkosti uhlov pri základni a presvedčte sa, že majú rovnakú veľkosť. Riešenie Tu.
určte veľkosti uhlov pri základni a presvedčte sa, že majú rovnakú veľkosť. Riešenie Tu. - Zostrojte hyperbolickú priamku
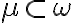 , ktorá je osou úsečky
, ktorá je osou úsečky 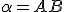 , kde
, kde 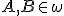 .
.
Návod:- Využitím Euklidovho tvrdenia T/I zostrojte hyperbolické rovnostranné trojuholník
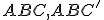 , kde
, kde 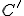 je súmerný bod podľa priamky
je súmerný bod podľa priamky 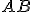 .
. - V trojuholníku
 zostrojte os prechádzajúcu vrcholmi
zostrojte os prechádzajúcu vrcholmi 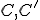 .
. - Využite Euklidove tvrdenia T/IX a T/X.
- Riešenie Tu.
- Využitím Euklidovho tvrdenia T/I zostrojte hyperbolické rovnostranné trojuholník
- Nájdite stred kružnice(pozrite si Euklidovo tvrdenie: Kniha III, T/I). Riešenie Tu.
- Zostrojte hyperbolickú kolmicu
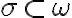 na hyperbolickú priamku
na hyperbolickú priamku 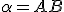 , ktorá prechádza bodom
, ktorá prechádza bodom 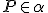 .
Pomocou dotyčníc k hPriamkam
.
Pomocou dotyčníc k hPriamkam 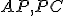 ukážte, že uhly pri päte kolmice sú pravé.
ukážte, že uhly pri päte kolmice sú pravé. - Zostrojte hyperbolickú kolmicu
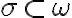 na hyperbolickú priamku
na hyperbolickú priamku 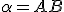 , ktorá prechádza bodom
, ktorá prechádza bodom 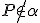 .
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
.
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
- Zostrojte hyperbolickú rovnobežku k hyperbolickej priamke
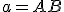 , ktorá prechádza bodom
, ktorá prechádza bodom 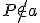 . Využite vlastnosť striedavých uhlov.
. Využite vlastnosť striedavých uhlov. - Zostrojte kružnicu vpísanú (resp. opísanú) do trojuholníka
 (pozrite si Euklidovo tvrdenie: Kniha IV, T/IV (resp. T/V)).
(pozrite si Euklidovo tvrdenie: Kniha IV, T/IV (resp. T/V)).
Poznámka
Euklidove tvrdenia využívané v tejto časti platia aj v hyperbolickej geometrii, keďže sú nezávislé na piatom Euklidovom postuláte.
Euklidove tvrdenia využívané v tejto časti platia aj v hyperbolickej geometrii, keďže sú nezávislé na piatom Euklidovom postuláte.
Verzia 3D
Trojdimenzionálna verzia programu GeoGebra umožňuje zobrazovať priestorové útvary v euklidovskej rovine.
Uvádzame ukážku konštrukcie Rez kockou od autora Vinkler.
Stiahnite si applet Tu
Na stránke http://www.geogebratube.org/ sa nachádza veľké množstvo edukačných materiálov.
Stiahnite si applet Tu
Na stránke http://www.geogebratube.org/ sa nachádza veľké množstvo edukačných materiálov.
Seminárne cvičenie
Cvičenie
-
Zostrojte rovnoramenný lichobežník
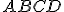 , ak poznáte dĺžky základní
, ak poznáte dĺžky základní 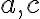 a veľkosť vnútorného uhla
a veľkosť vnútorného uhla  .
[Zdroj →]
Popis konštrukcie:
Otvorte si zadanie
Tu
Riešenie Tu
.
[Zdroj →]
Popis konštrukcie:
Otvorte si zadanie
Tu
Riešenie Tu -
Zostrojte trojuholník
 , ak je daná strana
, ak je daná strana 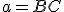 , ťažnica
, ťažnica 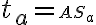 a veľkosť vnútorného uhla
a veľkosť vnútorného uhla 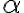 .
[Zdroj →, str. 20]
.
[Zdroj →, str. 20]
-
Zostrojte kružnicu, ktorá prechádza bodom
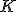 a dotýka sa polpriamok
a dotýka sa polpriamok 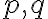 .
.
r -
Sústava dvoch rovníc.
Grafickou metódou v programe GeoGebra vyriešte sústavu dvoch rovníc: lineárnej a kvadratickej.
.
Otvorte si zadanie Tu a otvorte si postup konštrukcie (jednotlivé konštrukčné kroky) Tu .. -
Vytvorte konštrukciu, v ktorej po aktivácii začiarkavacích políčok sa budú zobrazovať grafy funkcií sin, cos, ...
Zároveň zostrojte dynamický bod, ktorý sa bude pohybovať po grafe týchto funkcií. Pozrite si ukážku Tu →
Otvorte si zadanie Tu.
Rozbor
Množina stredov všetkých kružníc, ktoré ležia vnútri uhla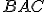 a dotýkajú sa polpriamok
a dotýkajú sa polpriamok 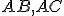 je os uhla
je os uhla 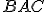 okrem bodu
okrem bodu 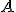 .
.
Na osi uhla si zvolíme ľubovoľný stred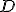 pomocnej kružnice
pomocnej kružnice  . Hľadaná kružnica a pomocná kružnica sú rovnoľahlé (podobné),
obidve majú stred na osi a dotýkajú sa ramien uhla.
. Hľadaná kružnica a pomocná kružnica sú rovnoľahlé (podobné),
obidve majú stred na osi a dotýkajú sa ramien uhla.
Pomocou rovnoľahlosti, ktorá bodu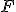 priradí bod
priradí bod 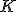 zostrojíme hľadanú kružnicu.
zostrojíme hľadanú kružnicu.
Množina stredov všetkých kružníc, ktoré ležia vnútri uhla
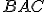 a dotýkajú sa polpriamok
a dotýkajú sa polpriamok 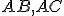 je os uhla
je os uhla 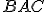 okrem bodu
okrem bodu 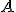 .
.
Na osi uhla si zvolíme ľubovoľný stred
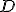 pomocnej kružnice
pomocnej kružnice  . Hľadaná kružnica a pomocná kružnica sú rovnoľahlé (podobné),
obidve majú stred na osi a dotýkajú sa ramien uhla.
. Hľadaná kružnica a pomocná kružnica sú rovnoľahlé (podobné),
obidve majú stred na osi a dotýkajú sa ramien uhla.
Pomocou rovnoľahlosti, ktorá bodu
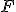 priradí bod
priradí bod 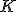 zostrojíme hľadanú kružnicu.
zostrojíme hľadanú kružnicu.
Padajúci rebrík
Rebrík opretý o stenu, ak stojí na hladkej podlahe, veľmi ľahko skĺzne dole - spadne.
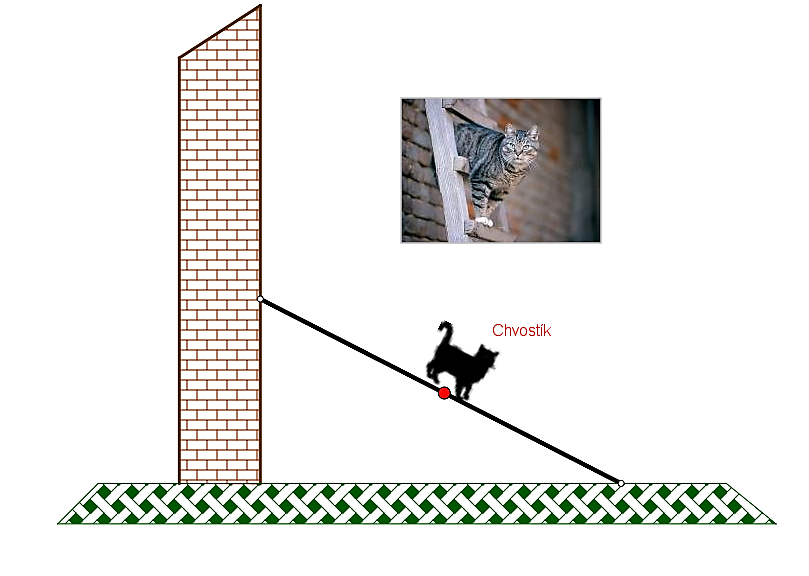
Po akej krivke sa pri tomto páde bude pohybovať mačka sediaca uprostred rebríka? Odpoveď nájdete Tu.
Rebrík opretý o stenu, ak stojí na hladkej podlahe, veľmi ľahko skĺzne dole - spadne.
Po akej krivke sa pri tomto páde bude pohybovať mačka sediaca uprostred rebríka? Odpoveď nájdete Tu.